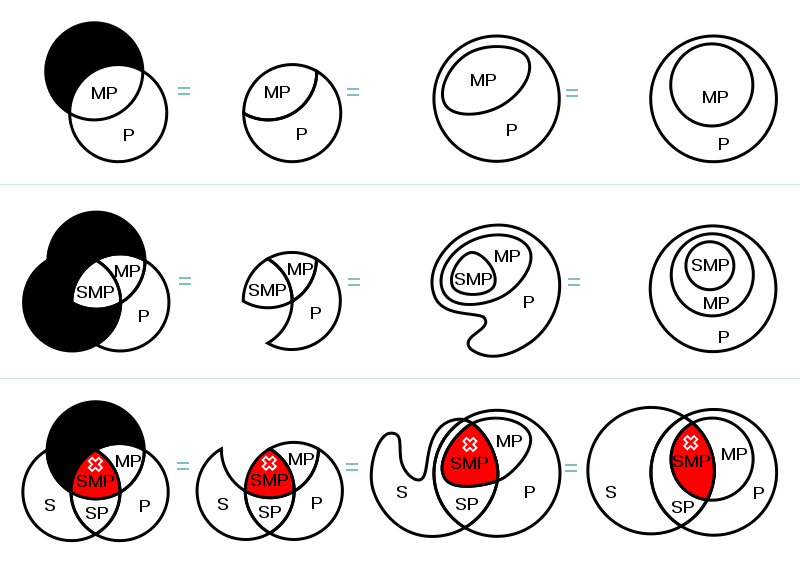
Diagrama de Euler

Um diagrama de Euler.

Um diagrama de Euler é similar a um diagrama de Venn, mas não precisa conter todas as zonas (onde uma zona é definida como a área de intersecção entre dois ou mais contornos). Assim, um diagrama de Euler pode definir um universo de discurso, isto é, ele pode definir um sistema no qual certas intersecções não são possíveis ou consideradas.

Assim, um diagrama de Venn contendo os atributos para Animal, Mineral e quatro patas teria que conter intersecções onde alguns estão em ambos animal, mineral e de quatro patas. Um diagrama de Venn, consequentemente, mostra todas as possíveis combinações ou conjunções.

Diagrama de euler dos tipos de objetos celestes

Introdução

Diagramas de Euler consistem em curvas simples fechadas (geralmente círculos) no plano que mostra os conjuntos. Os tamanhos e formas das curvas não são importantes: a significância do diagrama está na forma como eles se sobrepõem. As relações espaciais entre as regiões delimitadas por cada curva (sobreposição, contenção ou nenhuma) correspondem relações teóricas (subconjunto interseção e disjunção).

Cada curva de Euler divide o plano em duas regiões ou zonas estão: o interior, que representa simbolicamente os elementos do conjunto, e o exterior, o que representa todos os elementos que não são membros do conjunto. Curvas cujos interiores não se cruzam representam conjuntos disjuntos. Duas curvas cujos interiores se interceptam representam conjuntos que têm elementos comuns, a zona dentro de ambas as curvas representa o conjunto de elementos comuns a ambos os conjuntos (intersecção dos conjuntos). Uma curva que está contido completamente dentro da zona interior de outro representa um subconjunto do mesmo.

Os Diagramas de Venn são uma forma mais restritiva de diagramas de Euler. Um diagrama de Venn deve conter todas as possíveis zonas de sobreposição entre as suas curvas, representando todas as combinações de inclusão / exclusão de seus conjuntos constituintes, mas em um diagrama de Euler algumas zonas podem estar faltando. Essa falta foi o que motivou Venn a desenvolver seus diagramas.

Existia a necessidade de criar diagramas em que pudessem ser observadas, por meio de suposição, quaisquer relações entre as zonas não apenas as que são "verdadeiras".

História

Retrato em 1753 por Emanuel Handmann.

Existem algumas divergências sobre a real autoria dos diagramas : alguns autores consideram que o real criador foi Christian_Weise e não Euler. Como descrito por Venn o trabalho de Euler foi extensivamente usado em quase a totalidade das obras sobre lógica até então.

Porem, ele o critica muito em sua obra , Venn acaba por evidenciar que os diagramas de Euler não conseguiam representar corretamente os próprios silogismos que foram feitos para representar. Os diagramas não deixam espaço para a suposição já que representam apenas relações estritas. Desta forma Venn criou seu próprio diagrama a partir dos " velhos diagramas de Euler " e partir de então eles foram praticamente abandonados já que o foco tornaram-se os diagramas produzidos por Venn que vem sendo aperfeiçoados até hoje .

Aplicação

Os diagramas de Euler (em conjunto com os de Venn) são largamente utilizados em salas de aula para ensinar a teoria dos conjuntos no campo da matemática ou lógica matemática no campo da lógica.

Eles também podem ser utilizados para representar relacionamentos complexos com mais clareza , já que representa apenas as relações válidas.

Em estudos mais aplicados esses diagramas podem ser utilizados para provar/analisar silogismos que são argumentos lógicos para que se possa deduzir uma conclusão .

Também é possível a criação de mapas de karnaugh através de diagramas de Euler convertidos em diagramas de Venn.

Galeria