Teoria de grafos: diferenças entre revisões

Conteúdo apagado Conteúdo adicionado

Em linha

Revisão das 20h31min de 9 de setembro de 2003

     [[pl:Teoria graf%F3w]] pt:Teoria dos Grafos

(Esta página é uma cópia da respectiva em inglês. Estou traduzindo aos poucos.)

Teoria dos Grafos é um ramo da Matemática que examina as prorpiedades de grafos.

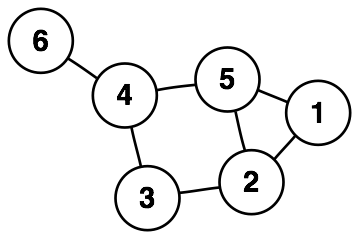A graph with 6 vertices and 7 edges.

Um grafo é um conjunto de pontos, chamados vértices ou nodos, conectados por linhas, chamadas de arestas or arcos. Dependendo da aplicação, arestas podem ou não ser direcionadas; arestas ligando um vértice a ele mesmo podem ou não serem permitidas e pode haver ou não uma função (numérica) peso nos vértices e/ou arestas. Se as arestas tem uma direção (indicada por uma setinha na representação gráfica) nós temos um grafo direcionado.

Estruturas que can be represented as graphs are ubiquitous, and many problems of practical interest can be formulated as questions about certain graphs. For example, the link structure of Wikipedia could be represented by a directed graph: the vertices are the articles in Wikipedia, and there's a directed edge from article A to article B if and only if A contains a link to B. Directed graphs are also used to represent finite state machines. The development of algorithms to handle graphs is therefore of major interest in computer science.

Definições de Grafos e Digrafos

The basic definitions in graph theory vary in the literature. Here are the conventions used in this encyclopedia.

A directed graph (also called digraph or quiver) consists of

a set V of vertices, and

a set E of edges, and

maps s, t : E → V, where s(e) is the source and t(e) is the target of the directed edge e.

An undirected graph (or graph for short) is given by

a set V of vertices,

a set E of edges,

a function w : E → P(V) which associates to each edge a two- or one-element subset of V, interpreted as the endpoints of the edge.

In a weighted graph or digraph, an additional function E → R associates a value with each edge, which can be considered its "cost"; such graphs arise in optimal route problems such as the traveling salesman problem.

"Graphical" representation (graph layout)

Graphs are often represented "graphically" as follows: draw a dot for every vertex, and for every edge draw an arc connecting its endpoints. If the graph is directed, indicate the endpoint of an edge by an arrow.

Note that this graphical representation (a layout) should not be confused with the graph itself (the abstract, non-graphical structure). Very different layouts can correspond to the same graph (see http://www.aisee.com/gallery/graph23.htm ). All that matters is which vertices are connected to which others by how many edges.

There are different approaches to graph layout and are considered under a branch of graph theory termed as "graph drawing". Some of the well known layouts are

spring layout - by using an energy function that is minimized so that nodes and edges spread out by repulsion.
orthogonal layout - layout with edges running horizontally or vertically, with approaches that reduce the number of edge crossovers and area covered. These are of great interest in the VLSI and chip design areas.
symmetric layout - these attempt to find symmetry groups within the graph
tree layout - these show a rooted tree like formation, suitable for trees (ie graphs without cycles)
hierarchical layouts - these attempt to find a source and sink within a directed graph and arrange the nodes in layers with most edges starting from the source and flowing in the direction of the sink.

Here are some examples of graph layouts:

Glossário Básico de Conceitos de Teoria dos Grafos

Um loop num grafo ou num digrafo é uma aresta e em E cujas terminações estão no mesmo vértice. Um digrafo ou grafo é chamado simple se não tem loops e existe no máximo uma entre quaiquer dois vértices.

The example graph pictured to the right is a simple graph with vertex set V = {1, 2, 3, 4, 5, 6} and edge set E = {{1,2}, {1,5}, {2,3}, {2,5}, {3,4}, {4,5}, {4,6}} (with the map w being the identity).

An edge connects two vertices; these two vertices are said to be incident to the edge. The valency (or degree) of a vertex is the number of edges incident to it, with loops being counted twice. In the example graph vertices 1 and 3 have a valency of 2, vertices 2,4 and 5 have a valency of 3 and vertex 6 has a valency of 1. If E is finite, then the total valency of the vertices is equal to twice the number of edges. In a digraph, we distinguish the out degree (=the number of edges leaving a vertex) and the in degree (=the number of edges entering a vertex). The degree of a vertex is equal to the sum of the out degree and the in degree.

Dois vértices são ditos adjacentes se existe uma aresta entre eles. No graof acima, os vértices 1 and 2 são adjacentes, mas os vértices 2 e 4 não são. O conjunto de vizinhos de um vértice consiste de todos os vértices adjacentes a ele. In the example graph, vertex 1 has two neighbors: vertex 2 and node 5. For a simple graph, the number of neighbors that a vertex has coincides with its valency.

Em computação, um grafo finito direcionado ou não (com, por exemplo, n vértices) é frequentemente representado pela sua matrix de adjacencias: uma matriz n-por-n cujo valor na linha i, coluna j dá o número de arestas do i-ésimo para o j-ésimo vértice.

A path is a sequence of vertices such that from each of its vertices there is an edge to the successor vertex. A path is considered simple if none of the vertices in the path are repeated. The length of a path is the number of edges that the path uses, counting multiple edges multiple times. The cost of a path in a weighted graph is the sum of the costs of the traversed edges. Two paths are independent if they do not have any vertex in common, except the first and last one.

In the example graph, (1, 2, 5, 1, 2, 3) is a path with length 5, and (5, 2, 1) is a simple path of length 2.

If it is possible to establish a path from any vertex to any other vertex of a graph, the graph is said to be connected. If it is always possible to establish a path from any vertex to any other vertex even after removing k-1 vertices, then the graph is said to be k-connected. Note that a graph is k-connected if and only if it contains k independent paths between any two vertices. The example graph above is connected (and therefore 1-connected), but not 2-connected.

A cycle (or circuit) is a path that begins and ends with the same vertex. Cycles of length 1 are loops. In the example graph, (1, 2, 3, 4, 5, 2, 1) is a cycle of length 6. A simple cycle is a cycle which has length at least 3 and in which the beginning vertex only appears once more, as the ending vertex, and the other vertices appear only once. In the above graph (1, 5, 2, 1) is a simple cycle. A graph is called acyclic if it contains no simple cycles.

An articulation point é um vértice que se removido desconecta o grafo. Uma ponte é uma aresta que se removida desconecta o grafo. A biconnected component is a maximal set of edges such that any two edges in the set lie on a common simple cycle. The girth de um grafo é o tamanho de menor ciclo simples do grafo. O girth de um grafo acíclico é definido como sendo infinito.

A tree is a connected acyclic simple graph. Sometimes, one vertex of the tree is distinguished, and called the root. Trees are commonly used as data structures in computer science (see tree data structure).

Uma floresta é um conjunto de árvores; equivalently, a forest is any acyclic graph.

Um subgrafo de um grafo G é um grafo cujo conjunto dos vértices é um subconjunto do conjunto de vértices G, cujo conjunto de arestas é um subconjunto do conjunto de arstas de G, e cuja função w é uma restrição da função de G.

Um spanning subgraph de um grafo G é um subgrafo com o mesmo conjunto de vértices de G. A spanning tree is a spanning subgraph that is a tree. Every graph has a spanning tree.

Um grafo completo is a simple graph in which every vertex is adjacent to every other vertex. The example graph is not complete. The complete graph on n vertices is often denoted by K_n. It has n(n-1)/2 edges (corresponding to all possible choices of pairs of vertices).

A planar graph is one which can be drawn in the plane without any two edges intersecting. The example graph is planar; the complete graph on n vertices, for n> 4, is not planar.

An Eulerian path in a graph is a path that uses each edge precisely once. If such a path exists, the graph is called traversable. An Eulerian cycle is a cycle with uses each edge precisely once. There is a dual to this concept: a Hamiltonian path in a graph is a path that visits each vertex once and only once; and a Hamiltonian cycle is a cycle which visits each vertex once and only once. The example graph does not contain an Eulerian path, but it does contain a Hamiltonian path. While determining whether a given graph has an Eulerian path or cycle is trivial, the same problem for Hamiltonian paths and cycles is extremely hard.

The null graph is the graph whose edge set and vertex set are empty.

An independent set in a graph is a set of pairwise nonadjacent vertices. In the example above, vertices 1,3, and 6 form an independent set and 3,5, and 6 are another independent set.

A clique (pronounced "click") in a graph is a set of pairwise adjacent vertices. In the example graph above, vertices 1, 2 and 5 form a clique.

A bipartite graph is any graph whose vertices can be divided into two sets, such that there are no edges between vertices of the same set. A graph can be proved bipartite if there do not exist any circuits of odd length.

A k-partite graph or k-colorable graph is a graph whose vertices can be partitioned into k disjoint subsets such that there are no edges between vertices in the same subset. A 2-partite graph is the same as a bipartite graph.

Graph Problems

Coloração de grafos: o Teorema das quatro cores

Problemas de rota:
- Sete pontes de Königsberg
- árvore de recobrimento mínimo
- Problema do caminho mínimo
- Route inspection problem (também conhecido como o "Problema do Carteiro Chinês")
- Problema do Caixeiro viajante

Fluxo:
- Teorema do mínimo corte-máximo fluxo

reconstruction conjecture

Problemas de Isomorfismo (casamento de grafos)
- Canonical Labeling
- subgraph isomorphism and monomorphisms
- Maximal common subgraph

Algoritmos Importantes

Generalizações

Num hypergraph uma aresta pode conectar mais que dois grafos.

Um grafo não-direcionado pode ser visto como um simplicial complex consisting of 1-simplices (the edges) and 0-simplices (the vertices). As such, complexes are generalizations of graphs since they allow for higher-dimensional simplices.

Todo grafo gera uma matroide, mas em geral o grafo não pode ser recuperado da sua matróide, logo, matroides não são generelizações reais de grafos.