Grafo de Folkman
| Grafo de Folkman | |
|---|---|
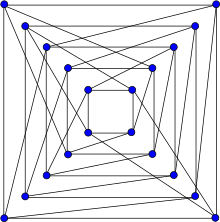 O grafo de Folkman | |
| Nomeado em honra a | J. Folkman |
| vértices | 20 |
| arestas | 40 |
| Raio | 3 |
| Diâmetro | 4 |
| Cintura | 4 |
| Número cromático | 2 |
| Índice cromático | 4 |
| Propriedades | Perfeito Hamiltoniano Semi-simétrico Bipartido Regular Euleriano |
No campo da matemática da teoria dos grafos o grafo de Folkman, nomeado em honra a Jon Folkman, é um grafo bipartido 4-regular com 20 vértices e 40 arestas.[1]
O grafo de Folkman é Hamiltoniano e tem número cromático 2, índice cromático 4, raio 3, diâmetro 4 e cintura 4. e é um grafo perfeito tanto 4-vértice-conectado quanto 4-aresta-conectado.
Propriedades algébricas[editar | editar código-fonte]
O grupo de automorfismo do grafo de Folkman age transitivamente em suas arestas, mas não em seus vértices. É o menor grafo não direcionado, que é aresta-transitivo e regular, mas não é vértice-transitivo.[2] Esses grafos são chamados semi-simétricos e foram estudados pela primeira vez por Folkman em 1967 que descobriu o grafo de 20 vértices, que agora é nomeado em sua honra.[3]
Como um grafo semi-simétrico, o gráfico de Folkman é bipartido, e seu grupo de automorfismo age transitivamente em cada um dos dois conjuntos de vértices da bipartição. No diagrama abaixo, indicando o número cromático do grafo, os vértices verdes não podem ser mapeados para os vermelhos por qualquer automorfismo, mas qualquer vértice vermelho pode ser mapeado em qualquer outro vértice vermelho e qualquer vértice verde pode ser mapeado em qualquer outro vértice verde.
O polinômio característico do grafo de Folkman é .
Galeria[editar | editar código-fonte]
-
O índice cromático do grafo de Folkman é 4.
-
O número cromático do grafo de Folkman é 2.
-
O grafo de Folkman é Hamiltoniano.
Referências
- ↑ Weisstein, Eric W. «Folkman graph» (em inglês). MathWorld
- ↑ Skiena, S. Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica. Reading, MA: Addison-Wesley, pp. 186-187, 1990
- ↑ FOLKMAN, J. (1967). «Regular line-symmetric graphs». Journal of Combinatorial Theory. 3. pp. 215–232. doi:10.1016/S0021-9800(67)80069-3




