Distância (teoria dos grafos)
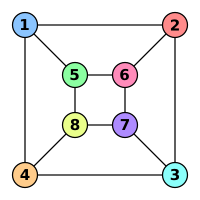
No campo da matemática da teoria dos grafos, a distância entre dois vértices em um grafo é o número de arestas em um caminho mínimo conectando eles.[1] Em outras palavras, denomina-se distância d(v, w) de um grafo como sendo o comprimento do menor caminho entre v e w.[2] Isso também é conhecido como distância geodésica[3] porque é o comprimento do grafo geodésico entre os dois vértices.[4] A distância entre dois vértices v1 e v2 é d se e somente se existe um caminho de comprimento d de v1 a v2 e nenhum caminho de v1 a v2 tem comprimento menor que d.[5] Se não existe caminho algum conectando dois vértices, ou seja, se eles pertencem a diferentes componentes conectados, então convencionalmente a distância entre eles é definida como infinita.[5]
Definições[editar | editar código-fonte]
O conjunto de vértices (de um grafo não-orientado) e a função de distância formam um espaço métrico, se e somente se o grafo é conexo.
Uma métrica definida sobre um conjunto de pontos em função das distâncias em um grafo definido sobre o conjunto é chamada uma métrica de grafo.
Medidas definidas em termos de distância[editar | editar código-fonte]
Há uma série de outras medidas definidas em termos de distância:
- A excentricidade de um vértice é a maior distância geodésica entre e qualquer outro vértice. Ela pode ser pensada como o quanto um nó é distante do nó mais distante dele no grafo.
- O raio de um grafo é a excentricidade mínima de qualquer vértice do grafo.
- O diâmetro de um grafo é a excentricidade máxima de qualquer vértice do grafo. Ou seja, ele é a maior distância entre qualquer par de vértices. Para achar o diâmetro de um grafo, primeiro encontre o caminho mínimo entre cada par de vértices. O maior comprimento de qualquer um desses caminhos é o diâmetro do grafo.
- Um vértice periférico em um grafo de diâmetro é aquele que dista de d de algum outro vértice, isto é, um vértice que alcança o diâmetro.
- Um vértice pseudo-periférico tem a propriedade que para qualquer vértice , se é tão longe quanto possível de , então é tão longe quanto possivel de . Formalmente, se a distância de a é igual à excentricidade de , então é igual à excentricidade de .
Algoritmo para encontrar vértices pseudo-periféricos[editar | editar código-fonte]
Muitas vezes algoritmos de matrizes esparsas periféricas precisam de um vértice de partida com uma grande excentricidade. Um vértice periférico seria perfeito, mas é muitas vezes difícil de calcular. Na maioria dos casos um vértice pseudo-periférico pode ser utilizado. Um vértice pseudo-periférico pode ser facilmente encontrado com o seguinte algoritmo:
- Escolha um vértice .
- Entre todos os vértices que estão distantes de o quanto possível, faça ser aquele com grau mínimo.
- Se então faça u=v e repita o passo 2, senão é um vértice pseudo-periférico.
Aplicações[editar | editar código-fonte]
Existem numerosas aplicações na teoria dos grafos nas quais se considera o conceito de distância:
- O índice de Wiener foi introduzido em 1947, sendo o primeiro índice de grafo introduzido na química. Em seu cálculo utiliza a distância entre dois átomos i e j, que é dada pela distância entre os vértices vi e vj que é igual ao número de arestas(ligações) considerando-se o menor caminho que conecte vi e vj.[6]
Referências
- ↑ «Distâncias». Consultado em 5 de novembro de 2010
- ↑ SZWARCFITER, Jayme Luiz (1988). Grafos e algoritmos computacionais. Rio de Janeiro: Campus. p. 39. ISBN 85-7001-341-8
- ↑ BOUTTIER, Jérémie;DI FRANCESCO,P.; GUITTER, E. (2003). «Geodesic distance in planar graphs». Nuclear Physics B. 663 (3). pp. 535–567. doi:10.1016/S0550-3213(03)00355-9. Consultado em 23 de abril de 2008.
Pela distância que quero dizer aqui distância geodésica ao longo do grafo, ou seja, o comprimento de qualquer caminho mínimo entre, digamos, duas faces dadas
- ↑ WEISSTEIN, Eric W. «Graph Geodesic». MathWorld--A Wolfram Web Resource. Wolfram Research. Consultado em 23 de abril de 2008.
O comprimento do grafo geodésico entre esses pontos d (u, v) é chamado a distância do grafo entre u e v
- ↑ a b «Caminhos mínimos». Consultado em 5 de novembro de 2010
- ↑ SILVA, Lucicleide Ribeiro da; FERREIRA, Márcia M. C. «Estudo do coeficiente de partição octanol-água de bifenilas policloradas (PCBs) utilizando parâmetros topológicos». Consultado em 5 de novembro de 2010





