Teoria da repulsão dos pares de elétrons da camada de valência
A Teoria da repulsão dos pares de elétrons da camada de valência é um modelo químico que busca predizer a geometria molecular por meio da repulsão eletrostática dos elétrons da camada de valência[1].
A teoria da VSEPR parte da premissa de que os pares de elétrons da camada de valência se repelem, adotando maneira tal que minimize essas repulsões, determinando, assim, sua geometria molecular.
A teoria de repulsão dos pares eletrônicos da camada de valência é criticada por apresentar resultados de natureza não quantitativa, limitando-se a prever a geometria das moléculas covalentes. Existem, entretanto, estudos mais complexos baseados na VSEPR já desenvolvidos[2].
História[editar | editar código-fonte]
Estudos que apresentassem alguma relação entre a geometria molecular e o número de elétrons da camada de valência (ligantes e não-ligantes) foram apresentados pela primeira vez na universidade de Oxford em 1940 por Nevil Sidgwick e Herbert Powell[3]. Em 1957, na University College London elaboraram uma teoria mais detalhada capaz de abranger as mais diversas geometrias moleculares[4].
Descrição[editar | editar código-fonte]
As regras que ditam a VSEPR envolvem predizer o arranjo dos pares de elétrons ao redor de um ou mais átomos centrais, elétrons esses ligados a dois ou mais átomos. A geometria dos átomos centrais, por sua vez, determina a geometria molecular.
O número de átomos ligados a um átomo central mais o número de pares de elétrons não-ligantes da camada de valência é conhecido por número estérico. Inicialmente, deve-se desenhar a estrutura de Lewis da molécula a ser analisada, de maneira a expor os pares de elétrons ligantes e não-ligantes. Conta-se, então, os pares de elétrons do átomo central. Quando ocorre ligação dupla ou tripla, os elétrons envolvidos nesta devem ser contados como um só par. Assumimos então que esses pares de elétrons estão dispostos ao redor de uma esfera e, em função da repulsão entre os mesmos, organizam-se de forma a ficarem o mais distantes uns dos outros como possível. É, logo, o número de pares de elétrons (número estérico e de pares não ligantes) que determina a estrutura adotada pela molécula.
Como exemplo, quando existem dois pares de elétrons na camada de valência, a repulsão desses pares na esfera faz com que os os pares de elétrons migrem para pólos opostos da molécula, adotando assim uma geometria linear. Se houverem três pares, para maximizar a distância entre os pares, forma-se a geometria trigonal plana. Quatro pares formam a geometria tetraédrica entre os pares de elétrons.
A geometria pode ser ainda refinada ao distinguir-se os pares de elétrons ligantes dos não-ligantes. Isso ocorre pois elétrons ligantes envolvidos em ligações sigma (uma vez que são compartilhados com um átomo adjascente) estão mais distantes do átomo central que os pares de elétrons não ligantes desse. Isso faz com que a repulsão entre pares não-ligantes seja maior que entre ligantes, alterando levemente os ângulos de maneira a compensar a proporção das repulsões.
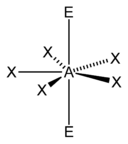
Essa consideração pode ser observada na molécula de água. Nela existem quatro pares de elétrons ao redor do oxigênio: dois ligantes e dois não-ligantes. O ângulo esperado de 109,5° é, na realidade 104,4°. Embora não seja muito nesse caso, quando tratamos de moléculas com mais pares de elétrons, a diferença pode tornar-se crítica. Quando temos cinco pares de elétrons, a geometria esperada seria trigonal bipiramidal. Nessa configuração. Duas posições ficam a 180° uma da outra, enquanto as outras três permanecem a 90° dessas duas e a 120° delas mesmas. Ocorre, que as duas posições mencionadas sofrem mais repulsão que as três. Em função disso, quando existem um ou mais pares não-ligantes, esses tendem a ocupar primeiro as três últimas posições.
Método A.X.E.[editar | editar código-fonte]
É um método de contar pares de elétrons que auxilia na aplicação da VSEPR. A letra A representa o átomo central, enquanto a letra E representa os pares de elétrons não ligantes e X representa os pares ligantes (lembrando que ligações duplas e triplas contam como apenas um par). A soma de X com E é o número estérico.
Baseado no número estérico, na distribuição de X’s e E’s, a VSEPR prediz a geometria molecular de acordo com a tabela a seguir:
| Num. Estérico |
Geometria básica 0 pares não ligantes |
1 par não ligante | 2 pares não ligantes | 3 pares não ligantes |
|---|---|---|---|---|
| 2 | ||||
| 3 |  |
 |
||
| 4 | 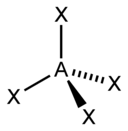 |
 |
 |
|
| 5 |  |
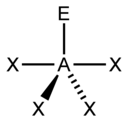 |
 |
 |
| 6 | 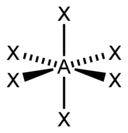 |
 |
 |
|
| 7 |  |
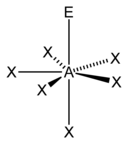 |
 |
|
| 8 | (IF8-) |
|||
| 9 | Trigonal prismática triapicada (ReH92-) |
| Número Estérico | Pares ligantes (X) | Pares ligantes (E) | Geometria | Ângulo das ligações | Exemplo | Imagem |
|---|---|---|---|---|---|---|
| linear | ||||||
| trigonal plana | ||||||
| angular | ||||||
| tetraédrica | 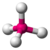 | |||||
| piramidal | ||||||
| angular | ||||||
| bipiramidal trigonal |  | |||||
| gangorra | ||||||
| forma de T | ||||||
| linear | ||||||
| octaédrica | 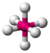 | |||||
| piramidal quadrada | ||||||
| quadrada plana | ||||||
| bipiramidal pentagonal | 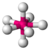 |

Quando os átomos que se ligam a A por X não forem os mesmos, a teoria ainda é válida, mas os ângulos formados podem ser levemente diferente dos previstos. Como exemplo, temos o C2H4 onde os ângulos não são extamente 120° como previsto devido a diferença nos átomos que se ligam a A (nesse caso um carbono da molécula).
Exemplos[editar | editar código-fonte]
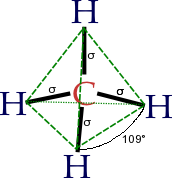
A molécula do metano (CH4) é tetraédrica porque o átomo central apresenta quatro pares de elétrons na camada de valência, todos ligantes a um átomo de hidrogênio cada[5].

A molécula de amônia (NH3) apresenta quatro pares de elétrons na camada de valência, sendo um deles não ligantes. É logo, piramidal. Uma vez que a repulsão entre pares não ligantes e pares envolvidos em ligações sigma é diferente, o ângulo entre os hidrogênios da amônia é distinto do ângulo entre os hidrogênios no metano.
Núméros estéricos maiores ou iguais a sete são incomuns, mas podem ser encontrados em compostos como o Heptafluoreto de iodo (IF7). A geometria base para o número estérico sete é a en:Pentagonal_bipyramidal_molecular_geometry[6].
Moléculas com elétrons ímpares na camada de valência[editar | editar código-fonte]
Quando se depara com um número ímpar de elétrons na camada de valência, aqueles não pareados podem ser encarados como “meio par”, comportando-se como um par, mas de maneira menos acentuada. Dessa maneira, a geometria resultante é intermediaria entre a molécula com o par inteiro e a com um par a menos. Um exemplo é o dióxido de nitrogênio (NO2), com um número ímpar de elétrons no átomo central N. Há, na realidade, um estado intermediário entre o NO2- (angular, 120°) e o NO2+ (linear, 180°), com ângulo de 134°[7].
O dióxido de cloro (ClO2) tem geometria intermediária entre o ClO22+ e o ClO22-.
Referências
- ↑ Jolly, W. L.,Modern Inorganic Chemistry, McGraw-Hill, 1984 ISBN 0-07-032760-2
- ↑ Box, Vernon G. S. (1997-03-17). «The Molecular Mechanics of Quantized Valence Bonds». Consultado em 28 de setembro de 2011
- ↑ http://www.jstor.org/pss/97507 N.V.Sidgwick and H.M.Powell, Proc.Roy.Soc.A 176, 153–180 (1940) Bakerian Lecture. Stereochemical Types and Valency Groups
- ↑ ^ R.J.Gillespie and R.S.Nyholm, Quart.Rev. 11, 339 (1957)
- ↑ "Angle Between 2 Legs of a Tetrahedron" – Maze5.net
- ↑ Pradyot Patnaik. Handbook of Inorganic Chemicals. McGraw-Hill, 2002, ISBN 0-07-049439-8
- ↑ Anslyn E.V. and Dougherty D.A., Modern Physical Organic Chemistry (University Science Books, 2006), p.57
