Algoritmos de estimação de distribuição

Algoritmos de estimação de distribuição (AED) são métodos evolutivos que utilizam técnicas de estimação de distribuição ao invés de operadores genéticos .

Fluxograma de um algoritmo de estimação de distribuição.

AED's são consequência dos algoritmos genéticos, sendo motivados pela deficiência destes, principalmente pela sua incapacidade de representar e manipular as dependências entre as variáveis. Este problema é conhecido como linkage problem.

Em seu trabalho seminal sobre algoritmos genéticos, Holland já havia reconhecido que, se a interação das variáveis fosse utilizada, certamente traria benefícios aos algoritmos genéticos. Esta fonte de informação, até então inexplorada, foi chamada de informação de ligação (linkage information).

Assim, para contornar estes obstáculos dos algoritmos genéticos, os AEDs representam explicitamente as dependências entre as variáveis através de modelos probabilísticos, como desde simples representação em vetores de probabilidades até modelos mais complexos, como rede bayesiana, estruturas em árvore (grafo), cadeias de Markov, entre outras. Os AEDs utilizam estes modelos probabilísticos como guias para desempenhar a busca em um determinado espaço de soluções.

Considere o seguinte exemplo de um AED. Seja uma população representada por vetores binários de comprimento 4. O AED pode empregar um único vetor composto por 4 probabilidades ($p_{1},p_{2},p_{3},p_{4}$) onde cada $p_{i}$ é a probabilidade da posição $i$ receber o valor 1. Usando este vetor de probabilidades é possível criar qualquer quantidade de soluções candidatas. Ao fim de cada geração, este vetor de probabilidades vai sendo atualizado segundo os melhores indivíduos da geração corrente.

Definição

Diferentemente dos algoritmos genéticos comuns, que utilizam operadores de recombinação e mutação para gerar novos indivíduos da população, os algoritmos de estimação de distribuição fazem uso de informações extraídas do conjunto de soluções promissoras presentes na população daquela geração. Uma maneira de utilizar a informação global sobre um conjunto de soluções promissoras é estimar sua distribuição e usar esta estimativa para gerar novos indivíduos. Os algoritmos que fazem uso deste princípio são chamados de Algoritmos de Estimação de Distribuição - AED (do inglês Estimation of distribution algorithm) . Essas distribuições contemplam diretamente as interações das variáveis que compõem o espaço de busca.

Formalmente, pode-se definir um AED como uma quádrupla da forma :

$AED=\{{\mathcal {C}},{\mathcal {P}}^{n},{\mathcal {S}},{\mathcal {E}}\}$

onde,

• ${\mathcal {C}}$: método para codificação dos indivíduos;
• ${\mathcal {P}}^{n}$: população de n indivíduos codificados;
• ${\mathcal {S}}$: operador estocástico (ou determinístico) para seleção;
• ${\mathcal {E}}$: Estimador da distribuição das melhores soluções (na iteração corrente).

Nota-se a eliminação dos componentes de recombinação, de mutação e suas probabilidades, em relação ao algoritmo genético (AG). No entanto, a tarefa de estimação deverá ser feita levando em conta a complexidade do modelo utilizado, como será visto nas seções seguintes. Dependendo do modelo de estimação utilizado, alguns parâmetros adicionais deverão ser informados.

Diferentemente do AG, em que as inter-relações (blocos construtivos) das variáveis representando os indivíduos são mantidas implicitamente, nos AEDs essas relações são expressadas explicitamente através da distribuição de probabilidade conjunta associada aos indivíduos selecionados em cada iteração.

A sequência estrutural do AED é bastante similar ao AG, diferindo na maneira como são gerados novos indivíduos. A seleção das soluções promissoras pode ser realizada de forma determinística ou estocástica, privilegiando indivíduos com melhores valores de fitness. A população pode ser amostrada integralmente a partir da distribuição de probabilidade; ou, visando maior exploração do ambiente, estipular uma porcentagem para adição de novos indivíduos gerados aleatoriamente; ou ainda substituindo alguns indivíduos da população anterior pelos novos indivíduos amostrados pela distribuição.

 $t\leftarrow 0$
 Gera população inicial ${\mathcal {P}}(t)$ aleatoriamente
 enquanto condição de parada não for satisfeita faça
    Avalição: $\Phi ({\mathcal {P}}(t))$
    Seleção: ${\mathcal {S}}({\mathcal {P}}(t))$
    Estimação da distribuição de probabilidades, ${\mathcal {E}}$, do conjunto selecionado
    Amostre a nova população ${\mathcal {P}}(t+1)$ a partir de ${\mathcal {E}}$
    $t\leftarrow t+1$
 retorne o melhor indivíduo encontrado.

Exemplos de critérios de parada são: um número fixo de iterações, um número fixo de diferentes avaliações de fitness dos indivíduos e ausência de melhorias do melhor indivíduo em um certo número de iterações subsequentes.

O passo fundamental nesta classe de algoritmos é como estimar a distribuição das soluções promissoras. Na realidade, a estimação da distribuição de probabilidade conjunta associada às variáveis, a partir de soluções promissoras selecionadas, constitui o gargalo destes algoritmos. Será necessário então um balanço entre a precisão desta estimação e seu custo computacional.

Tipos de AEDs

Os algoritmos presentes nesta classe diferenciam-se basicamente pela forma como a estimação é realizada, sendo classificados de acordo com a complexidade do modelo probabilístico utilizado: variáveis sem dependência; dependência aos pares; dependência multivariada e modelos de mistura .

A seguir, serão apresentadas algumas abordagens de AEDs, tanto para problemas de otimização em espaços discretos, quanto em espaços contínuos. Esta revisão será organizada considerando os quatro níveis de complexidade do modelo probabilístico, citados acima e utilizados para extrair as interdependências das variáveis que formam o espaço de busca.

Modelos sem dependências

A maneira mais simples de estimativa é supor que as variáveis do problema são independentes, ou seja, não há qualquer tipo de relação entre elas (veja figura ao lado). Formalmente, a distribuição de probabilidade conjunta é fatorizada como o produto de n distribuições de probabilidades independentes e univariadas:

$p(x)=\prod _{i=1}^{n}p(x_{i})$

onde x é o conjunto de soluções promissoras, em um espaço de busca n-dimensional, selecionadas para a estimação.

O modelo de estimação utilizado para gerar novos indivíduos contém o conjunto de frequências de valores das variáveis que representam a solução no conjunto selecionado. Assim, estas frequências são usadas para guiar a busca, gerando novos indivíduos, variável por variável de acordo com os valores de frequência. Dessa forma, os blocos construtivos de primeira ordem são reproduzidos e mesclados eficientemente . Algoritmos baseados neste mecanismo são indicados para problemas em que as variáveis não possuem interação mútua .

AED sem dependência. Os nós representam as variáveis do problema e a ausência de arestas entre os nós indica que não há dependência entre as variáveis.

Exemplos de algoritmos que fazem uso deste modelo probabilístico, no espaço de variáveis discretas, são: o UMDA ( Univariate Marginal Distribution Algorithm) , onde cada distribuição marginal univariada é estimada pelas respectivas frequências marginais; o PBIL (Population Based Incremental Learning) , que utiliza a regra de aprendizado hebbiano para a atualização do vetor de probabilidades, a partir do conjunto de soluções selecionadas; e o CGA (Compact Genetic Algorithm) , que atualiza o vetor de probabilidades p(x) a partir de uma competição entre dois indivíduos amostrados com base em p(x), sendo p(x) deslocado em direção ao indivíduo vencedor.

Para o caso contínuo, supõe-se que a função densidade de probabilidade conjunta segue uma distribuição normal n-dimensional, que é fatorizada pelo produto de n densidades normais unidimensionais e independentes . O problema então consiste na estimação dos parâmetros da distribuição. Formalmente, para o caso de uma distribuição normal, a função densidade de probabilidades é descrita por:

$f(x;\mu ,\Sigma )=\prod _{i=1}^{n}f_{\mathcal {N}}(x_{i};\mu _{i},\sigma _{i}^{2})$

onde $\mu _{i}$ denota a média da i-ésima variável e $\sigma _{i}^{2}$ sua variância. O algoritmo UMDA foi estendido ao espaço de variáveis contínuas (UMDA$_{c}$) . Aqui, a cada iteração o algoritmo busca por uma função densidade que melhor se ajuste à variável, obtendo seus parâmetros pela estimativa da máxima verossimilhança. Já o algoritmo SHCLVND (Stochastic Hill Climbing with Learning by Vectors of Normal Distributions) atualiza os parâmetros da distribuição normal, média e variância, pela regra de Hebb para a média e uma política de redução para a variância.

Modelos com dependência aos pares

Embora a suposição de independência entre as variáveis seja satisfeita para alguns problemas, nem sempre esta hipótese é verificada, sendo então necessário levar em consideração algumas dependências. Quando a dependência aos pares é considerada, estabelece-se um compromisso entre a precisão e o custo computacional. A distribuição de probabilidades conjunta é fatorizada como:

$p(x)=\prod _{i=1}^{n}p(x_{i}|x_{j_{(i)}})$

onde $x_{j_{(i)}}$ é a variável da qual $x_{i}$ é dependente.

Enquanto os algoritmos que consideram variáveis independentes estimam apenas os parâmetros do modelo, na dependência aos pares a aprendizagem paramétrica é estendida para a aprendizagem da estrutura do modelo de dependência (um grafo direcionado).

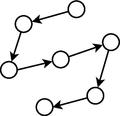
No contexto discreto, o MIMIC (Mutual Information Maximizing Input Clustering) usa uma cadeia simples de distribuição (veja figura a seguir) que maximiza a informação mútua das variáveis vizinhas (posições na cadeia), através de uma abordagem gulosa, que, embora eficiente, não garante a otimalidade global. A utilização de árvores de dependência foi formalizada por no COMIT (Combining Optimizers with Mutual Information Trees), que utiliza uma rede bayesiana com estrutura em árvore que é construída pelo algoritmo proposto por . O algoritmo BMDA (Bivariate Marginal Distribution Algorithm) implementa uma floresta (um conjunto de árvores de dependência mutuamente independentes) como modelo probabilístico. Uma floresta pode ser interpretada como uma generalização do conceito de árvores de dependência. O algoritmo usa o teste Chi-quadrado de Pearson para determinar quais variáveis serão conectadas.

• 
  Modelo probabilístico com dependência aos pares. Algoritmo MIMIC.
• 
  Algoritmo COMIT.
• 
  Algoritmo BMDA.

No caso contínuo, o MIMIC foi estendido para problemas com variáveis contínuas, supondo que o modelo de probabilidades é uma distribuição normal bivariada que utiliza um resultado de para calcular e usar a entropia como medida para determinar dependência entre duas variáveis.

Algoritmos desta família reproduzem e mesclam blocos construtivos de segunda ordem eficientemente, obtendo sucesso na aplicação junto a problemas lineares e quadráticos .

Modelos com múltiplas dependências

Apesar de modelos que consideram dependência aos pares serem eficientes em certos cenários, em problemas multivariados ou com alta sobreposição de blocos construtivos, este tipo de modelo se mostra insuficiente para representar o espaço das boas soluções. Esta classe de problemas requer estimativas mais completas, mesmo à custa de uma maior demanda computacional.

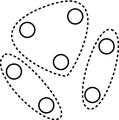
No algoritmo ECGA (Extended Compact Genetic Algorithm) , no domínio discreto, as variáveis são divididas em grupos, cujas variáveis de um mesmo grupo (bloco construtivo) são independentes entre si, como mostra a figura abaixo. A divisão dos grupos é feita por um procedimento guloso que utiliza a métrica Minimum description length (MDL) . A distribuição de probabilidades conjunta foi codificada por uma rede bayesiana no algoritmo EBNA (Estimation of Bayesian Networks Algorithm) . Neste método, a estrutura da rede é construída por uma estratégia gulosa de busca local utilizando alguma métrica para medir a qualidade da rede, como BIC (Bayesian Information Criterion), K2 com penalidades (K2+pen) ou teste de (in)dependência condicional.

• 
  Modelos gráficos com múltiplas dependências. Algoritmo ECGA.
• 
  Modelos gráficos dos algoritmos EBNA e BOA.

A métrica de pontuação Bayesian-Dirichlet (BD) foi utilizada no algoritmo BOA (Bayesian Optimization Algorithm) , que, de forma incremental, vai adicionando novas arestas no grafo até que não haja melhorias na qualidade do modelo. Com o objetivo de reduzir a cardinalidade do espaço de busca, os autores propuseram restringir, a um número fixo, a quantidade de pais para cada nó da rede bayesiana.

No contexto de variáveis contínuas, o EMNA$_{global}$ (Estimation Multivariate Normal Algorithm) é baseado na estimação de uma função densidade normal multivariada em cada geração. Apesar do grande número de parâmetros a serem estimados, os cálculos envolvidos são simples.

Os algoritmos desta classe se distinguem das outras abordagens pela capacidade de representar as interações multivariadas presentes no problema. Apesar destes algoritmos demandarem alto custo computacional, devido ao aprendizado de modelos mais complexos, o número de avaliações de fitness tende a ser reduzido significativamente . Por isso, a complexidade computacional total tende a ser reduzida para problemas mais complexos, em que o cálculo da função-objetivo é computacionalmente oneroso.

Modelos de mistura

No caso de problemas multimodais, outros modelos probabilísticos mais flexíveis podem ser empregados. Modelos de mistura fazem uso do procedimento de agrupamento das soluções promissoras e posicionam distribuições de probabilidade junto a cada agrupamento. O modelo pode ser descrito como segue:

$p(x)=\sum _{i=1}^{K}\pi _{i}p_{i}(x)$

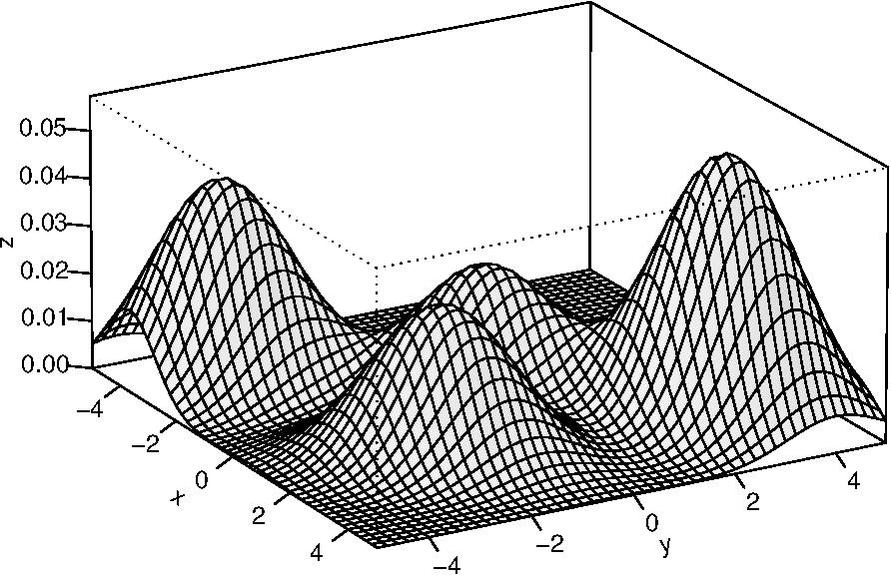
onde $\pi _{i}$ representa o peso do i-ésimo componente da mistura e $p_{i}(x)$ é a distribuição de probabilidade do i-ésimo grupo criado pelo método de agrupamento de dados. O peso de cada componente juntamente com os parâmetros das distribuições de probabilidades são obtidos por algum procedimento dedicado, como o algoritmo EM (Expectation-Maximization) . A figura a seguir apresenta um modelo de mistura gaussiano arbitrário composto de quatro componentes.

Um dos principais obstáculos desses métodos é a necessidade de conhecer, de antemão, o número de componentes, onde cada grupo busca representar um pico da função a ser otimizada. De fato, o número de componentes do modelo dependerá de quão multimodal o problema é. No entanto, existem formas de estimar este parâmetro, como por exemplo, através dos critérios de informação: Bayesian Information Criterion, Akayke Information Criterion, entre outros.

No caso discreto, é possível criar um modelo de mistura em que cada componente é uma rede bayesiana, como o EMDA (Estimation of Mixtures of Distributions Algorithm) descrito por , embora este tipo de estimador seja mais aplicado para o caso contínuo.

Para o espaço de variáveis contínuas, propuseram o algoritmo AMix (Adaptative Gaussian Mixture'), que utiliza um modelo de mistura adaptativo. O número de componentes do modelo de mistura pode variar durante a execução do algoritmo. O algoritmo EDA$_{OGMM}$ emprega um modelo de mistura gaussiano que utiliza uma forma de treinamento ao longo do tempo, o que reduz significativamente o custo computacional do algoritmo. Além disso, auto-ajusta a número de componentes de mistura no decorrer do processo de busca.

Aplicações

Os AEDs vem sendo aplicados em uma gama de problemas de diversas áreas de conhecimento. Dentre as aplicações podemos destacar: seleção de atributos, evolução de pesos de redes neurais MLP, geração de regras SE-ENTÃO para sistemas nebulosos, expressão gênica, análise de estrutura de proteínas, em problemas de otimização multiobjetivo e de otimização dinâmica.

Ligações externas

• Texto sobre Algoritmos Genéticos^{[ligação inativa]}