Evolvente
Este artigo não cita fontes confiáveis. (Fevereiro de 2014) |
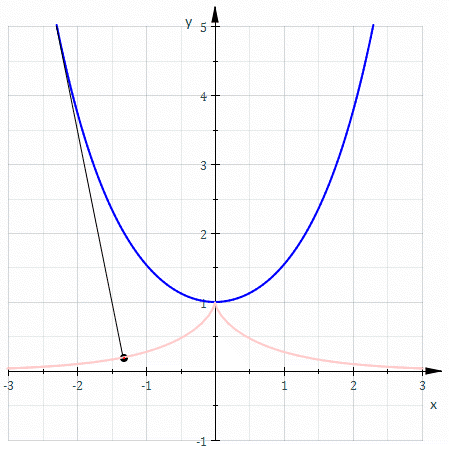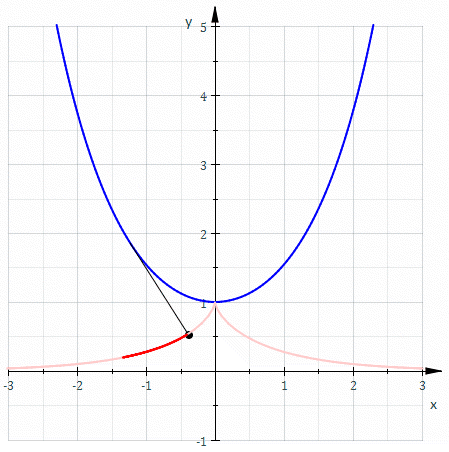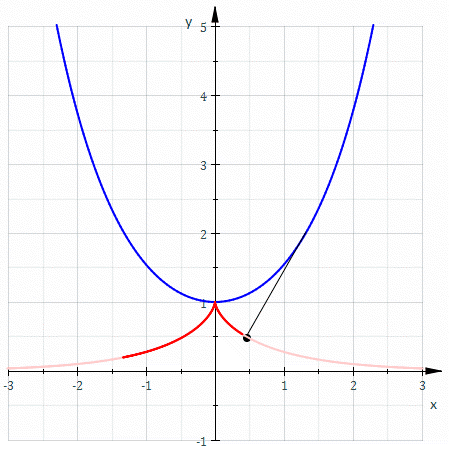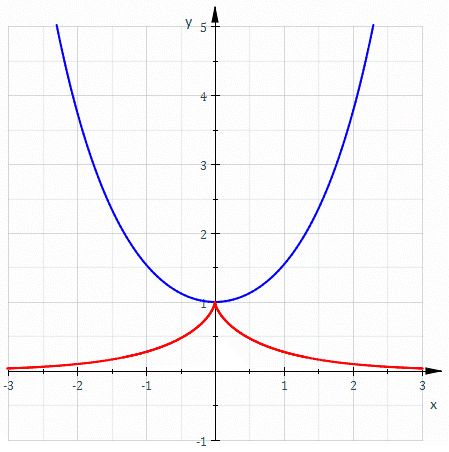
Na geometria diferencial de curvas, uma evolvente é uma curva obtida de outra dada curva anexando a esta um cordão tenso imaginário e traçando um ponto da corda ao enrolá-la na curva; ou, ao contrário, ao desenrolá-la. É uma rolete na qual a curva rolante é uma linha reta contendo o ponto gerador. Por exemplo, uma evolvente é aproximadamente o caminho seguido por um espirobol quando a corda de ligação é enrolada no poste. Se o poste tem seção transversal circular, então a curva descrita pela bola é uma evolvente do círculo.
Alternativamente, outra forma de construir a evolvente de uma curva é substituir a corda esticada por um segmento de reta que é tangente à curva em uma extremidade, enquanto a outra extremidade traça a evolvente. O comprimento do segmento de reta é alterado pelo mesmo comprimento de arco que é percorrido sobre a curva quando o ponto tangente move-se ao longo da curva.
A evoluta de uma evolvente é a curva original, subtraidas as porções de curvatura zero ou indefinida. Ver as ilustrações evoluta e evolvente.
Se a função é uma parametrização natural da curva (i.e. para todo s), então : parametriza a evolvente.
Curva paramétrica
[editar | editar código-fonte]As equações de uma curva evolvente para uma função parametricamente definida ( x(t) , y(t) ) são:
Exemplos
[editar | editar código-fonte] |
 (reversa, desenrolando) |
 |
Evolvente de um círculo
[editar | editar código-fonte]A evolvente de um círculo tem uma forma semelhante a uma espiral de Arquimedes.
- Em coordenadas cartesianas a evolvente de um círculo tem as equações paramétricas
onde é o raio do círculo e é um parâmetro
- Em coordenadas polares a evolvente de um círculo tem as equações param[etricas
onde é o raio do círculo e é um parâmetro.
A evolvente de um círculo pode ser dada na forma
- .
Leonhard Euler propos o uso da evolvente de um círculo para a forma dos dentes de uma engrenagem, a forma que é atualmente usada na maioria delas, denominadas engrenagens evolventes.
Evolvente de uma catenária
[editar | editar código-fonte]A evolvente de uma catenária pelo seu vértice é uma tractriz. Em coordenadas cartesianas a evolvente é dada por
onde t é um parâmetro e sech é a secante hiperbólica (1/cosh(x)).
Derivada
Com
temos
e .
Substituindo
resulta .
Evolvente de uma cicloide
[editar | editar código-fonte]Uma evolvente de uma cicloide é uma cicloide congruente. Em coordenadas cartesianas a curva é dada por
onde t é o ângulo e r o raio.
Aplicação
[editar | editar código-fonte]A evolvente possui algumas propriedades que a tornam fundamental para a indústria de engrenagens: se duas engrenagens engatadas possuem dentes com perfil evolvente, elas formam um sistema de engrenagens evolventes. Suas taxas de rotação relativas são constantes enquanto os dentes estão engrenados, e o contato ocorre sempre ao longo de um segmento de reta, denominado linha de ação. Com dentes de outras formas as velocidades de rotação e as forças transmitidas são intermitentes, ocasionando portanto vibrações, ruídos e desgaste excessivo. Por esta razão quase a totaalidade das engrenagens atualmente produzidas possuem dentes com a forma evolvente.
A evolvente de um círculo é também uma forma fundamental em compressores, pois um compressor espiral pode ser construído baseado nesta forma. Compressores espirais fazem menos barulho que compressores convencionais, sendo também mais eficientes.
Ver também
[editar | editar código-fonte]Ligações externas
[editar | editar código-fonte]- «Mathworld» (em inglês)




![{\displaystyle X[x,y]=x-{\frac {x'\int _{a}^{t}{\sqrt {x'^{2}+y'^{2}}}\,dt}{\sqrt {x'^{2}+y'^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/203e22b2482eac10aaea0446f9a3e69e82db9674)
![{\displaystyle Y[x,y]=y-{\frac {y'\int _{a}^{t}{\sqrt {x'^{2}+y'^{2}}}\,dt}{\sqrt {x'^{2}+y'^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9f2233dc9b36793a05d1afd06e88265b393567b)


















