Leonhard Euler
Leonhard Paul Euler (pronúncia em português: ['ɔjler]; pronúncia em alemão: [ˈɔʏlɐ] (ⓘ), pronúncia local: [ˈɔɪlr̩] (ⓘ); Basileia, 15 de abril de 1707 – São Petersburgo, 18 de setembro de 1783) foi um matemático e físico suíço de língua alemã que passou a maior parte de sua vida na Rússia e na Alemanha.[2] Fez importantes descobertas em várias áreas da matemática como o cálculo e a teoria dos grafos. Também introduziu muitas das terminologias da matemática moderna e da notação matemática, particularmente na análise matemática, assim como no conceito de função matemática.[3] Também é reconhecido por seus trabalhos na mecânica, dinâmica de fluidos, óptica, astronomia e teoria da música.[4]
Euler é considerado um dos mais proeminentes matemáticos do século XVIII e também é considerado como um dos grandes matemáticos de todos os tempos, assim como Isaac Newton, Arquimedes e Carl Friedrich Gauss.[5] Foi um dos mais prolíficos matemáticos, calcula-se que toda a sua obra reunida teria entre 60 e 80 volumes de quartos.[6] Viveu a maior parte da vida em São Petersburgo, na Rússia, e em Berlim, que na época era capital da Prússia.
Uma declaração atribuída a Pierre-Simon Laplace manifestada sobre Euler na sua influência sobre a matemática: "Leiam Euler, leiam Euler, ele é o mestre de todos nós".[7][8]
Vida[editar | editar código-fonte]
| Física |
|---|
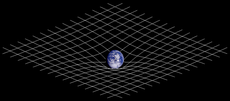 |
| Curvatura Espaço-Tempo |
|
Divisões elementares |
|
História |
|
Grandezas físicas
|
|
Físicos Mecânica Clássica
Eletromagnetismo
Mecânica Quântica Relatividade |
Primeiros anos[editar | editar código-fonte]
Leonhard Paul Euler [AFI: [ˈɔʏlɐ], ⓘ] nasceu no dia 15 de abril de 1707 em Basileia, na Suíça, filho do pastor calvinista Paul Euler e Margaret Brucker, filha de um pastor. Teve duas irmãs mais novas, Anna Maria e Maria Magdalena.[9] Depois do nascimento de Leonhard, sua família mudou da cidade de Basiléia para a cidade de Riehen, onde viveu a maior parte de sua infância. Paul Euler era amigo da família Bernoulli; Johann Bernoulli, que era então o matemático mais importante da Europa, foi a influência mais relevante da vida do jovem Leonhard.
Sua educação primeira foi dada por seu pai Paul que lhe ensinou matemática. Em 1720, aos treze anos, Euler ingressou na pequena Universidade de Basileia que possuía um famoso departamento de estudos da matemática liderado por Johann Bernoulli, irmão de Jacob Bernoulli. Johann inicialmente recusou-se a dar aulas particulares a Euler, oferecendo então um valioso conselho de como estudar por conta própria.[10]
Em 1722, recebe o grau de Mestre em Artes, e no seu exame deu um discurso em latim comparando as filosofias de Descartes e Newton.[11] Nesta altura, já recebia, aos sábados à tarde, lições de Johann Bernoulli,[12] que rapidamente descobriu o seu talento para a matemática.
Euler nesta altura estudava teologia, grego e hebraico, pela vontade de seu pai - para mais tarde se tornar pastor. Porém Johann Bernoulli resolveu intervir e convenceu Paul Euler que o seu filho estava destinado a ser um grande matemático.[13]
Em 1726, Euler completou a sua dissertação sobre propagação do som intitulada de De Sono.[14] Na época estava tentando, sem sucesso, obter um cargo na Universidade de Basileia. Em 1727 entrou pela primeira vez na competição premiada da Academia de Paris; o problema do ano era encontrar a melhor maneira de colocar os mastros num navio. Ganhou o segundo lugar, perdendo para Pierre Bouguer, mais tarde conhecido como “o pai da arquitetura naval”. Euler, entretanto, ganharia o prêmio anual doze vezes.[15]
São Petersburgo[editar | editar código-fonte]
Na época os dois filhos de Johann Bernoulli, Daniel e Nicolaus, foram trabalhar na Academia Russa de Ciências. No dia 10 de julho de 1726, Nicolaus morreu de apendicite após viver um ano na Rússia, e quando Daniel assumiu o cargo do irmão na divisão de matemática e física da universidade, ele indicou a vaga em fisiologia, que ocupava até então, para ser preenchida por seu amigo Euler. Em novembro de 1726 Euler aceitou ansiosamente a oferta, porém atrasou a viagem para São Petersburgo enquanto tentava uma vaga como professor de física na Universidade de Basileia.[16]

Leonhard chegou em São Petersburgo no dia 17 de maio de 1727. Foi promovido a assistente do departamento médico da academia para uma vaga no departamento de matemática. Foi apresentado por Daniel Bernoulli com quem frequentemente trabalhava em uma estreita parceria. Euler aprendeu russo e instalou-se em São Petersburgo. Também aceitou um trabalho adicional como médico na Marinha Russa.[17]
A Academia de S. Petersburgo, sob a política de Pedro I da Rússia, tinha intenção de melhorar a educação na Rússia e corrigir a defasagem no campo das ciências do país em relação à Europa Ocidental. Como resultado, a instituição criou um programa de internacionalização, com o objetivo de atrair estudantes estrangeiros como Euler. A instituição possuía vultosos recursos financeiros e uma biblioteca abrangente, planejada a partir das bibliotecas privadas da nobreza e do príncipe Pedro. Poucos estudantes foram inscritos na academia para diminuir a grade curricular e enfatizar a pesquisa, oferecendo para o corpo docente tempo e liberdade para prosseguir o questionamento científico.[15]
A benfeitora da Academia, Catarina I da Rússia, que tinha continuado a política progressiva da gestão anterior, morreu no dia em que Euler foi viajar. A aristocracia, em seguida, teve mais poder durante os dois anos de mandato do Pedro II. A nobreza, desconfiada dos cientistas estrangeiros da Academia, cortou-lhes o financiamento e causou dificuldades para Euler e seus colegas.
As condições melhoraram um pouco depois da morte de Pedro II, e Euler tornou-se professor de física em 1731, pela sua classificação no ranking da escola. Dois anos mais tarde, Daniel Bernoulli partiu para Basileia depois de ter sido perseguido com a censura e pela hostilidade que enfrentou em St. Petersburgo, e, assim, Euler o substituiu como professor de Matemática.[18]
No dia 7 de janeiro de 1734, Leonhard Euler se casou com Katharina Gsell, filha de Georg Gsell, um pintor da Academia Gymnasium.[19] O jovem casal construiu uma casa perto do rio Neva. Tiveram treze filhos, dos quais apenas cinco sobreviveram à infância.[20]
Berlim[editar | editar código-fonte]
Preocupado com a contínua turbulência na Rússia, Euler deixou São Petersburgo em 19 de Julho de 1741, para assumir uma posição em Berlim que tinha sido ofertada por Frederico II da Prússia. Viveu por vinte e cinco anos em Berlim, onde escreveu 380 artigos. Em Berlim publicou dois de seus mais renomados trabalhos: A Introductio in analysin infinitorum, um texto sobre funções matemáticas publicado em 1748 e o Institutiones calculi differentialis,[21] publicado em 1755 sobre cálculo diferencial.[22] No mesmo ano foi eleito um membro estrangeiro da Academia Real das Ciências da Suécia.
Entretanto, é convidado para ser tutor de Friederike Charlotte de Brandenburgo-Schwedt, a Princesa de Anhalt-Dessau e sobrinha de Frederico II, o Grande. Euler escreveu mais de 200 cartas dirigidas à princesa, que mais tarde foram compiladas num volume best-selling intitulado Cartas de Euler sobre diferentes assuntos da Filosofia natural para uma Princesa Alemã.[23] Este trabalho incorpora exposições sobre vários assuntos pertencentes à física e matemática, dando também a conhecer as perspectivas religiosas e a própria personalidade do seu autor. Este livro veio a ser o mais lido de todas as suas obras matemáticas, e foi publicado dentro da Europa e nos Estados Unidos. A popularidade das "Cartas" atesta a capacidade de Euler para comunicar sobre assuntos científicos de maneira eficaz para um público leigo, uma rara habilidade para um cientista dedicado à pesquisa.[22]
Apesar da imensa e impressionante contribuição para a Academia de Berlim, provocou a ira de Frederico II, o que o forçou a abandonar Berlim. O rei da Prússia tinha um grande círculo social de intelectuais em sua corte e ele permaneceu um matemático sem sofisticações e informal, tanto em seu trabalho como na vida pessoal. Euler foi simples, religioso devoto que nunca questionou a existência de ordens ou crenças convencionais, em muitas situações, opositor direto de Voltaire – que tinha uma posição privilegiada na corte de Frederick. Euler não era um debatedor qualificado e muitas vezes fez dela um ponto para discutir assuntos sobre os quais ele sabia pouco, fazendo dele o alvo frequente de sagacidade de Voltaire.[22] Frederick também comentou decepcionado com Euler as habilidades práticas de engenharia:
Citação: Eu quero ter um jato de água em meu jardim: Euler calculava a força necessária das rodas para transportar a água para o reservatório, de onde deve voltar por meio de canais, até finalmente jorrar em Sanssouci. Meu moinho foi geometricamente construído e não poderia levantar um gole de água mais perto do que a quinze passos até o reservatório. A vaidade das vaidades! A vaidade da geometria![24]

Problemas na visão[editar | editar código-fonte]
A acuidade visual de Euler piorou ao longo de sua carreira matemática. Em 1738, três anos depois de sofrer uma febre quase fatal em 1735, tornou-se quase cego do olho direito, mas, ao invés de se lamentar, apresentou um trabalho meticuloso sobre cartografia para a Academia de São Petersburgo. A visão de Euler se agravou durante a sua estada na Alemanha, na medida em que Frederico II da Prússia se referia a ele como "Cyclops". Euler mais tarde desenvolveu uma catarata no olho esquerdo, deixando-o quase totalmente cego poucas semanas depois de sua descoberta em 1766. No entanto, sua condição parece ter pouco efeito sobre sua produtividade, compensando com suas habilidades de cálculo mental e de memória fotográfica. Por exemplo, Euler conseguia repetir a Eneida de Virgílio, do começo ao fim, sem hesitação. Com a ajuda de seus escribas, a produtividade de Euler em muitas áreas de estudo, na verdade, aumentou. Produziu, em média, um artigo matemático durante todas as semanas do ano 1775.[6]
Retorno à Rússia e falecimento[editar | editar código-fonte]
Em 1760, com o alastramento da Guerra dos Sete Anos, a fazenda de Euler em Charlottenburg foi devastada pelo avanço das tropas russas. Como punição, o general Ivan Petrovich Saltykov indenizou pelos danos causados na propriedade de Euler, depois da tzarina Isabel da Rússia adicionar um pagamento de 4 000 rublos - um valor exorbitante na época.[26] A situação política russa se estabilizaria após a ascensão de Catarina, a Grande ao trono, quando em 1766, Euler aceita um convite para voltar a Academia de St. Petersburgo. Suas condições foram bastante exorbitantes – um salário anual de 3 000 rublos, uma pensão para a sua esposa e a promessa de cargos de alto escalão para os seus filhos. Todas destas condições foram atendidas. Viveu o resto de sua vida na Rússia. Contudo, sua segunda estadia no país foi marcada por uma tragédia: Um incêndio em Santo Petersburgo em 1771 destruiu a sua casa, e quase o matou. Em 1773, faleceu a sua esposa Katharina após 40 anos de casamento.
Três anos depois da morte de sua esposa, Euler casou com sua meia-irmã, Salome Abigail Gsell (1723–1794).[27] Este casamento durou até o fim de sua vida. Em 1782 foi eleito membro honorário estrangeiro da Academia de Artes e Ciências dos Estados Unidos.[28]
Em Santo Petersburgo no dia 18 de setembro de 1783, depois de um almoço com sua família, Leonhard estava discutindo sobre a descoberta de um novo planeta da época, chamado Urano e sua órbita com o também acadêmico Anders Johan Lexell, quando sucumbiu por causa de uma hemorragia cerebral. Morreu algumas horas depois.[29] Jacob von Staehlin-Storcksburg escreveu no obituário de Leonard para a Academia de Santo Petersburgo e o matemático russo Nicolaus Fuss, um de seus discípulos, escreveram uma detalhada eulogia,[30] em que ele encomendou uma assembleia em memória. Em sua eulogia para a Academia Francesa, o filósofo e matemático francês marquês de Condorcet, escreveu:

Citação: il cessa de calculer et de vivre—... ele terminou de calcular e de viver.[31]
Foi enterrado próximo de Katharina no cemitério luterano de Smolensk na Ilha de Vassiliev. Em 1785, a Academia de Ciências da Rússia pôs um busto de mármore de Leonhard Euler em um pedestal próximo à reitoria e, em 1837, esculpiram uma lápide para Euler. Para comemorar os duzentos e cinquenta anos do nascimento dele, a lápide foi transferida em 1956, junto com seus restos mortais, para a necrópole do século XVIII no mosteiro Alexander Nevsky, o cemitério Tikhvin.[32]
Contribuições para a matemática[editar | editar código-fonte]
| Parte de uma série de artigos sobre a |
| constante matemática e |
|---|
 |
| Propriedades |
| Aplicações |
| Definir e |
| Pessoas |
Euler trabalhou em quase todas as áreas da matemática: geometria, cálculo infinitesimal, trigonometria, álgebra e teoria dos números, bem como deu continuidade na física newtoniana, teoria lunar e outras áreas da física. É uma figura seminal na história da matemática, e suas obras, muitas das quais são de interesse fundamental, ocupam entre 60 e 80 volumes. O nome de Euler está associado a um grande número de temas. Euler é o único matemático que tem dois números em homenagem a ele: O número e, aproximadamente igual a 2,71828, e a constante de Euler-Mascheroni γ (gama) por vezes referida apenas como "constante de Euler", aproximadamente igual a 0,57721. Não se sabe se γ é racional ou irracional.[33]
Notação matemática[editar | editar código-fonte]
Euler introduziu e popularizou várias convenções de notação matemática através de seus numerosos e amplamente divulgados livros didáticos. Mais notavelmente, introduziu o conceito de uma função, e foi o primeiro a escrever f(x) para denotar a função f aplicada ao argumento x. Também introduziu a notação moderna para as funções trigonométricas, a letra e para a base do logaritmo natural (agora também conhecido como número de Euler), a letra grega Σ (sigma maiúsculo) para somatórios e a letra i para representar a unidade imaginária.[34] O uso da letra grega π (pi) para designar a razão entre a circunferência de um círculo e o seu diâmetro também foi popularizado por Euler, embora não tenha se originado com ele.[35]
Análise[editar | editar código-fonte]
O desenvolvimento do cálculo infinitesimal estava na vanguarda da pesquisa matemática do século XVIII, e os amigos, de Euler, da Família Bernoulli - foram responsáveis por grande parte do progresso inicial no campo. Graças à sua influência, estudar cálculo tornou-se o foco principal do trabalho de Euler. Embora algumas das provas de Euler não sejam aceitáveis para os padrões modernos de rigor matemático[36] (em particular a sua dependência em relação ao princípio da generalidade da álgebra), suas ideias levaram a muitos grandes avanços. Euler é bem conhecido na análise pela sua utilização frequente e desenvolvimento da série de potência, a expressão de funções como somas de um número infinito de termos, tais como:
Notavelmente, Euler provou diretamente as expansões em séries de potência para e e a função da tangente inversa. (Prova indireta através da técnica de séries de potência inversa foi dada por Newton e Leibniz. (Entre 1670 e 1680) Seu uso ousado da série de potência lhe permitiu resolver o famoso problema de Basileia em 1735 (ele forneceu um argumento mais elaborado em 1741):[36]

Euler introduziu o uso da função exponencial e logaritmo em provas analíticas. Descobriu maneiras de expressar diversas funções logarítmicas utilizando séries de potência, e conseguiu definir logaritmos para números negativos e complexos, ampliando consideravelmente o leque de aplicações matemáticas de logaritmos.[34] Também definiu a função exponencial para números complexos, e descobriu a sua relação com as funções trigonométricas.
Para qualquer número real φ (tida como radianos), a fórmula de Euler afirma que o complexo satisfaz a função exponencial.
Um caso especial da fórmula acima é conhecida como a identidade de Euler,
chamada de "a fórmula mais notável em matemática", por Richard Feynman,[37] por seus usos individuais das noções de adição, multiplicação, exponenciação, e igualdade, e os usos individuais da constantes 0, 1, e, i e π. Em 1988, os leitores da Mathematical Intelligencer votaram como sendo "a fórmula matemática mais bela de todos os tempos". No total, Euler foi responsável por três das cinco melhores fórmulas nessa enquete.[38]
Pafnuti Tchebychev escreveu: "Euler foi o início de todas as pesquisas que compõem a teoria geral dos números." A maioria dos matemáticos do século XVIII se dedica ao desenvolvimento de análise, mas Euler carregava a antiga paixão aritmética ao longo de sua vida. Por causa de seu interesse na teoria dos números, a mesma foi revivida até o final do século.
Euler continuou com suas pesquisas feitas anteriormente (sob influência de Diophantus), uma série de hipóteses separadas sobre os números naturais. Euler provou rigorosamente essas hipóteses, muito generalizadas, e as combinou em uma interessante teoria dos números. Introduziu na matemática "função de Euler" crítica e formulada com a ajuda do "teorema de Euler." Euler criou a teoria dos resíduos quadráticos e comparações, apontando para o último critério de Euler.
Euler Introduziu a função zeta de Riemann, uma generalização, que mais tarde recebeu o nome de Bernhard Riemann verdadeiro. Euler provocou a sua expansão:
- ,
onde o produto é feita sobre todos os primos, . Devido a isso, provou que a soma do inverso simples diverge.[39]
A fórmula de De Moivre é uma conseqüência da fórmula de Euler. Além disso, Euler elaborou a teoria do nível superior das funções transcendentes pela introdução da função gama e introduziu um novo método de solução das funções quárticas. Também descobriu um meio de calcular integral com limites complexos, o prenúncio do desenvolvimento da análise complexa moderna. Ele, igualmente, inventou o cálculo das variações incluindo suas melhores soluções pela Equação de Euler-Lagrange.
Euler iniciou também o uso de métodos de análise para resolução dos problemas da teoria dos números.[40]
Teoria dos números[editar | editar código-fonte]
O interesse de Euler na teoria dos números pode ser atribuído à influência de Christian Goldbach, seu amigo na Academia de São Petersburgo. Muitos dos primeiros trabalhos de Euler na teoria dos números foram baseadas nas obras de Pierre de Fermat. Euler desenvolveu algumas das ideias de Fermat, e refutou algumas das suas conjeturas.
Euler ligou a natureza da distribuição privilegiada, com ideias de análise. Conseguiu provar que a soma dos recíprocos dos primos divergem. Ao fazer isso, descobriu a conexão entre a função zeta de Riemann e os números primos, o que é conhecido como a fórmula do produto Euler para a função zeta de Riemann.
Euler provou identidades de Newton, Pequeno teorema de Fermat, teorema de Fermat em somas de dois quadrados, e fez contribuições distintas ao Teorema de Fermat-Lagrange. Inventou também a função φ totiente (n). Usando as propriedades desta função, generalizou o teorema de Fermat ao que é hoje conhecido como o teorema de Euler. Contribuiu de forma significativa para a teoria dos números perfeitos, que havia fascinado os matemáticos desde Euclides. Euler também conjeturou a lei da reciprocidade quadrática. O conceito é considerado como um teorema fundamental da teoria dos números, e suas ideias pavimentaram o caminho para o trabalho de Carl Friedrich Gauss.[41]
Teoria dos grafos[editar | editar código-fonte]

Em 1736, Euler resolveu o problema conhecido como sete pontes de Königsberg. A cidade de Königsberg, Prússia, foi construída no rio Pregel, e incluiu duas grandes ilhas que estavam conectadas entre si e ao continente por sete pontes. O problema era o de decidir se é possível seguir um caminho que atravessa cada uma das pontes exatamente uma vez e retornar ao ponto de partida. Esta solução é considerada como sendo o primeira teorema da teoria dos grafos, especificamente da teoria gráfica planar.[42]
Euler também descobriu a fórmula V - E + F = 2 relacionando o número de vértices, arestas e faces de um poliedro convexo e, portanto, de um grafo planar. A constante nesta fórmula é agora conhecida como a característica de Euler para o gráfico (ou objeto de cálculo), e está relacionada ao gênero do objeto. O estudo e generalização desta fórmula foram, especificamente através de Augustin-Louis Cauchy, Simon Antoine Jean L'Huillier, estando na origem da topologia.[43][44]
Matemática aplicada[editar | editar código-fonte]
Alguns dos maiores sucessos de Euler foram na resolução de problemas do mundo real analiticamente, e em descrever inúmeras aplicações do números de Bernoulli, série de Fourier, diagramas de Venn, os números de Euler, as constantes e e pi, frações contínuas e integrais. Integrou cálculo diferencial de Leibniz com o de Newton, e as ferramentas que tornaram mais fácil de aplicar o cálculo de problemas físicos desenvolvidos. Fez grandes progressos na melhoria da aproximação numérica de integrais, inventando o que hoje é conhecido como aproximações de Euler. As mais notáveis dessas aproximações são o método de Euler e a fórmula de Euler. Também facilitou o uso de equações diferenciais, em particular, a introdução da constante de Euler-Mascheroni.
Um dos interesses mais incomuns de Euler foi a aplicação de ideias matemáticas na música. Em 1739, escreveu o Tentamen novae theoriae musicae, na esperança de, eventualmente, incorporar a teoria musical como parte da matemática. Esta parte de seu trabalho, no entanto, não recebeu grande atenção e já foi descrita como muito matemática para músicos e demasiado musical para matemáticos.[45]
Trabalhos na física e na astronomia[editar | editar código-fonte]
| Mecânica clássica |
|---|
 Diagramas de movimento orbital de um satélite ao redor da Terra, mostrando a velocidade e aceleração. |
|
Cinemática |
|
História |
|
Colisões |
|
Sistemas Clássicos |
Euler ajudou a desenvolver o modelo de viga de Euler-Bernoulli, que se tornou um marco da engenharia. Além de aplicar com sucesso as suas ferramentas analíticas para problemas em mecânica clássica, Euler também aplicou essas técnicas para problemas celestes. Seu trabalho em astronomia foi reconhecido por uma série de prêmios da Paris Academy ao longo de sua carreira. Suas realizações incluem determinar com grande precisão as órbitas de cometas e outros corpos celestes, compreender a natureza dos cometas, e calcular a paralaxe do Sol. Seus cálculos também contribuíram para o desenvolvimento de tabelas de longitude precisas.[46]
Além disso, Euler fez importantes contribuições na óptica. Discordou da teoria corpuscular de Newton da luz nos Opticks, que era então a teoria prevalecente. Seus trabalhos sobre óptica em 1740 ajudaram a garantir que a teoria ondulatória da luz proposta por Christiaan Huygens se tornasse o modo dominante de pensamento, pelo menos até o desenvolvimento da teoria quântica da luz.[47]
Em 1757 publicou um importante conjunto de equações, que agora são conhecidas como as Equações de Euler.[48] Na forma diferencial, as equações são:
Onde:
- ρ é o densidade do fluido;
- u é o vetor de velocidade do fluido, com os eixos u, v e w;
- E = ρ e + ½ ρ (u2 + v2 + w2) é a energia total por unidade (volume), com e sendo a energia interna por unidade de massa para o fluido;
- p é a pressão;
- denota o produto tensorial,e;
- 0 sendo o elemento zero.
Flambagem[editar | editar código-fonte]
Euler também é conhecido na engenharia pela fórmula de flambagem sob carga crítica de um suporte ideal, calculada a partir do seu comprimento e rigidez à flexão:[49]
Onde:
- F = força máxima ou crítica (carga vertical da coluna);
- E = módulo de elasticidade;
- I = momento de inércia de área;
- L = comprimento sem suporte da coluna;
- K = fator de comprimento de coluna efetiva, no qual os valores dependem das condições da extremidade do suporte da coluna, como abaixo:
- Para ambas as extremidades presas (articulações, livres para rotação), K = 1,0.
- Para ambas as extremidades fixadas, K = 0,50.
- Para uma das extremidades fixas e a outra extremidade livre para rotação, K = 0,699…
- Para uma das extremidades fixas e a outra livre para mover de forma lateral, K = 2,0.
- K L é o comprimento efetivo da coluna.
Ângulos de Euler[editar | editar código-fonte]

Em 1765, em seu livro "A Teoria do movimento dos corpos sólidos", Euler matematicamente descreveu a cinemática de um corpo rígido de tamanho finito. Introduziu na matemática o teorema de Euler de ângulos de rotação. Seu nome também é usado na fórmula de cinemática da distribuição de velocidade em um sólido, conhecido como as equações (Euler - Poisson), dinâmica de corpo rígido, um dos três casos gerais integráveis no problema da dinâmica de um corpo rígido com um ponto fixo.
Euler generalizou o princípio da mínima ação, um conjunto bastante confuso e apontou para a sua importância fundamental na mecânica. Infelizmente, não revelou a natureza do princípio variacional, mas, no entanto, atraiu a atenção de físicos, que mais tarde descobriram que o seu papel fundamental na natureza era válido.
Euler trabalhou no campo da mecânica celeste. Lançou as bases da teoria de perturbações, mais tarde completadas por Pierre Simon Laplace, e desenvolveu uma teoria muito precisa do movimento da Lua. Esta teoria provou ser adequada para resolver o problema urgente de determinar a longitude no mar.
Principais obras de Euler nesta área:
- "A teoria do movimento da Lua", 1753;
- "A teoria do movimento dos planetas e cometas" (latim Theoria motus Planetarum et cometarum), 1774;
- "A nova teoria do movimento da Lua", 1772.
Euler estudou o campo gravitacional não só esférico, mas os corpos elipsoidais, o que representa um significativo passo em frente.[50]
Lógica[editar | editar código-fonte]
Euler é também creditado por utilizar as curvas fechadas para ilustrar os argumentos do silogismo em 1768. Estes diagramas são conhecidos como diagramas de Euler.[51]

Um Diagrama de Euler é uma forma diagramática de representar conjuntos e suas relações. Este diagrama consiste de curvas fechadas simples (geralmente círculos) no plano que representam os conjuntos. Cada curva de Euler divide o plano dentro de duas regiões ou "zonas": o interior, simbologicamente representa os elementos do conjunto, e o exterior que representa todos os elementos que não são membros do conjunto. As partes das formas das curvas não são importantes: o significado do diagrama é em como eles se coincidem. As relações espaciais entre as fronteiras entre regiões de cada curva (sobrepõem, contenção ou nem um dos casos) correspondem às relações aos conjuntos teóricos (interseção, subconjunto e conjuntos disjuntos).[52] Desde então, eles têm também sido adotados por outros campos curriculares, como leitura.[53]
Frederico II, o Grande e Voltaire[editar | editar código-fonte]
Porém Euler tinha caído em desgraça junto de Frederico II, que lhe chamava “ciclope” – numa referência ao seu defeito físico. Já desde 1735, Euler sofria de alguns problemas de saúde, como febres altas. Em 1738, perdeu a visão do olho direito, devido ao excesso de trabalho. Mas tal infelicidade não diminuiu em nada a sua produção Matemática.
Euler nunca teve problemas em produzir trabalhos de diferentes géneros, como por exemplo, material para livros-textos para as escolas russas. Geralmente escrevia em latim, mas também em francês, embora a sua língua de origem fosse o alemão. Tinha uma enorme facilidade para línguas, como bom suíço que era, o que lhe facilitava muito a vida nas diversas viagens que fazia, como era costume dos matemáticos do século XVIII. Em 1749, depois de 7 anos de trabalho e quase cem anos após a morte de Fermat, conseguiu provar a teoria de Fermat.
Em 1759, com a morte de Maupertuis (1698-1759), o lugar de diretor da Academia foi dado a Euler. Ao saber que outro cargo, o de presidente, tinha sido oferecido ao matemático d'Alembert, com quem tinha tido algumas divergências sobre questões científicas, Euler ficou bastante perturbado. Apesar de d'Alembert não ter aceite o cargo, Frederico continuou a implicar com Euler, que farto de tal situação, aceitou o convite feito por Catarina, a Grande de voltar para a Academia de S. Petersburgo.
Euler e outros matemáticos[editar | editar código-fonte]
Euler e d'Alembert[editar | editar código-fonte]
O trabalho entre Euler e d'Alembert sempre convergiu no mesmo sentido. Os seus interesses eram quase os mesmos, apesar de ter havido alguma controvérsia entre eles sobre o problema das membranas vibrantes, em 1757, cuja solução da equação de Bessel, Euler conseguiu obter, o que ocasionou um afastamento. Mas, com a teoria dos números houve um grande apoio por parte de d’Alembert a Euler.
A contribuição de Euler para a teoria dos logaritmos não se restringiu à definição de expoentes, como usamos hoje. Trabalhou, também, no conceito de logaritmo de números negativos.
Enquanto se mantinha ocupado a pesquisar matemática em Berlim, d’Alembert pesquisava em Paris.
Em 1747, Euler escreveu a este matemático explicando corretamente a questão dos logaritmos dos números negativos. Mas ao contrário do que seria de se esperar, a fórmula formulada por Euler, válida para qualquer ângulo (em radianos), não foi compreendida por Bernoulli nem por d'Alembert pois, para estes, os logaritmos de números negativos eram reais, o que não é verdade já que se tratam de números imaginários puros.
Através da sua identidade – mais tarde conhecida como Igualdade de Euler – é possível observar que os logaritmos de números complexos, reais ou imaginários, também são números complexos. Usando as identidades de Euler é também possível expressar quantidades como sen(1 + i) ou cos(i), na forma usual para números complexos. Desta maneira, vê-se que ao efetuar operações transcendentes elementares sobre os números complexos, os resultados são números complexos.
Assim sendo, Euler foi capaz de demonstrar que o sistema de números complexos é fechado sob as operações transcendentes elementares, enquanto d’Alembert sugerira que o sistema de números complexos era algebricamente fechado.
Euler e Fermat[editar | editar código-fonte]
Tanto Fermat como Euler sentiram-se bastante interessados pela teoria dos números. Embora não haja qualquer livro sobre este assunto, Euler escreveu cartas e artigos sobre vários aspetos desta teoria. Entre elas encontram-se as conjeturas apresentadas por Fermat, que foram derrubadas por Euler. Duas dessas conjeturas foram:
- Os números da forma 22n + 1 são sempre primos;
- Se p é primo e a um inteiro, então ap – a é divisível por a.
A primeira foi derrubada em 1732 com o auxílio do seu domínio em computação, evidenciando que 225 + 1 = 4 294 967 297 é fatorizável em 6 700 417 * 641. No entanto, no recurso a um contraexemplo para deitar por terra a segunda conjetura, Euler também errou, apesar do erro só ter sido descoberto em 1966, dois séculos depois e com o auxílio de um computador.
Euler também realizou a demonstração de uma conjetura bastante conhecida, denominada como Pequeno teorema de Fermat. Tal demonstração foi apresentada numa publicação em 1736, denominada Commentarii.
Posteriormente, demonstrou uma afirmação mais geral do Pequeno teorema de Fermat, que veio a chamar-se Função de Euler. Mas, contrariando o que seria esperado, Euler não foi capaz de demonstrar o Último Teorema de Fermat, embora provasse a impossibilidade de soluções inteiras de xn + yn = zn para n = 3.
Em 1747, definiu mais 27 números amigáveis, que se juntaram aos três já conhecidos por Fermat. Mais tarde aumentou o número para 60. Euler também provou que todos os números perfeitos pares são da forma dada por Euclides, 2n-1(2n – 1), onde 2n – 1 é primo. Se existe ou não um número ímpar perfeito foi uma questão levantada por Euler e Goldbach, através de correspondência, ainda hoje sem resposta.
Comemorações[editar | editar código-fonte]

Euler foi destaque na sexta série de notas de 10 francos suíços e em numerosos selos suíços, alemães e russos. O asteroide 2002 Euler foi nomeado em sua honra. Também é comemorada pela Igreja Luterana em seu Calendário dos Santos em 24 de maio, ele era um devoto cristão (crente na infalibilidade bíblica), que escreveu apologéticas e argumentou energicamente contra os ateus proeminentes de seu tempo.[54]
Em 15 de abril de 2013, os 306 anos de Euler foi comemorado com um Google Doodle.[55]
Obras[editar | editar código-fonte]
- Dissertatio physica de sono (Dissertação sobre a física do som) (Basileia, 1727, in quarto)
- Mechanica, sive motus scientia analytice; expasita (São Petersburgo, 1736, in 2 vols. quarto)
- Ennleitung in die Arithmetik (ibid., 1738, in 2 vols. octavo), in German and Russian
- Tentamen novae theoriae musicae (ibid. 1739, in quarto)
- Methodus inveniendi limas curvas, maximi minimive proprictate gaudentes (Lausanne, 1744, in quarto)
- Theoria motuum planetarum et cometarum (Berlin, 1744, in quarto)
- Beantwortung, &c., ou Answers to Different Questions respecting Comets (ibid., 1744, in octavo)
- Neue Grundsatze, c., ou New Principles of Artillery, traduzido para o inglês por Benjamin Robins, com notas e ilustrações (ibid., 1745, in octavo)
- Opuscula varii argumenti (ibid., 1746-1751, in 3 vols. quarto)
- Novae et carrectae tabulae ad loco lunae computanda (ibid., 1746, in quarto)
- Tabulae astronomicae solis et lunae (ibid., quarto)
- Gedanken, &c., ou Thoughts on the Elements of Bodies (ibid. quarto)
- Rettung der gall-lichen Offenbarung, &c., Defence of Divine Revelation against Free-thinkers (ibid., 1747, in 4t0)
- Introductio it analysin infinitorum (Lausanne, 1748, in 2 vols. 4t0)
- Scientia navalis, seu tractatus de construendis ac dirigendis navi bus (St Petersburg, 1749, in 2 vols. quarto)
- Theoria motus lunae (Berlin, 1753, in quarto)
- Dissertatio de principio mininiae actionis, 'una cum examine objectionum cl. prof. Koenigii (ibid., 1753, in octavo)
- Institutiones calculi differentialis, cum ejus usu in analysi Intuitorum ac doctrina serierum (ibid., 1755, in 410)
- Constructio lentium objectivarum, &c. (St Petersburg, 1762, in quarto)
- Theoria motus corporum solidoruni seu rigidorum (Rostock, 1765, in quarto)
- Institutiones,calculi integralis (St Petersburg, 1768-1770, in 3 vols. quarto)
- Lettres a une Princesse d'Allernagne sur quelques sujets de physique it de philosophic (St Petersburg, 1768-1772, in 3 vols. octavo)
- Anleitung zur Algebra, ou Introduction to Algebra (ibid., 1770, in octavo); Dioptrica (ibid., 1767-1771, in 3 vols. quarto)
- Theoria motuum lunge nova methodo pertr.arctata (ibid., 1772, in quarto)
- Novae tabulae lunares (ibid., in octavo); La théorie complete de la construction et de la manteuvre des vaisseaux (ibid., .1773, in octavo)
- Eclaircissements svr etablissements en favour taut des veuves que des marts, without a date
- Opuscula analytica (St Petersburg, 1783-1785, in 2 vols. quarto). See Rudio, Leonhard Euler (Basel, 1884)
Referências
- ↑ Leonhard Euler (em inglês) no Mathematics Genealogy Project
- ↑ Jesse Russell; Ronald Cohn. Leonhard Euler. Book on Demand; 2012 [cited 2013]. ISBN 978-5-510-52879-4.
- ↑ Dunham 1999, p. 17
- ↑ Saint Petersburg (1739). «Tentamen novae theoriae musicae ex certissimis harmoniae principiis dilucide expositae»
- ↑ The Countless Achievements of a Math Master; By David Brown; Washington Post Staff Writer; Monday, April 9, 2007 washingtonpost.com
- ↑ a b Finkel, B.F. (1897). «Biography- Leonard Euler». The American Mathematical Monthly. 4 (12). 300 páginas
- ↑ Dunham 1999, p. xiii "Lisez Euler, lisez Euler, c'est notre maître à tous."
- ↑ The quote appeared in Gugliemo Libri's review of a recently published collection of correspondence among eighteenth-century mathematicians: Gugliemo Libri (January 1846), Book review: "Correspondance mathématique et physique de quelques célèbres géomètres du XVIIIe siècle, … " (Mathematical and physical correspondence of some famous geometers of the eighteenth century, … ), Journal des Savants, page 51. From page 51: " … nous rappellerions que Laplace lui même, … ne cessait de répéter aux jeunes mathématiciens ces paroles mémorables que nous avons entendues de sa propre bouche : 'Lisez Euler, lisez Euler, c'est notre maître à tous.' " ( … we would recall that Laplace himself, … never ceased to repeat to young mathematicians these memorable words that we heard from his own mouth: 'Read Euler, read Euler, he is our master in everything.)
- ↑ Ioan James. Remarkable Mathematicians: From Euler to Von Neumann. Cambridge University Press; 2002. ISBN 978-0-521-52094-2. p. 2.
- ↑ Vladimir B. Ginzburg. Prime Elements of Ordinary Matter, Dark Matter & Dark Energy: Beyond Standard Model & String Theory. Universal-Publishers; 2007 [cited 2013]. ISBN 978-1-58112-946-5. p. 161.
- ↑ Semen Grigorʹevich Gindikin; Simon Gindikin (2007), Tales of Mathematicians and Physicists, ISBN 978-0-387-48811-0, Springer, p. 175
- ↑ James, Ioan (2002). Remarkable Mathematicians: From Euler to von Neumann. [S.l.]: Cambridge. 2 páginas. ISBN 0-521-52094-0
- ↑ Michael J. Bradley. Mathematics Frontiers: 1950 to Present. Infobase Publishing; 2006. ISBN 978-0-7910-9722-9. p. 104-105.
- ↑ Ian Bruce. «Euler's Dissertation De Sono : E002. Translated & Annotated» (PDF). 17centurymaths.com. Consultado em 14 de setembro de 2011
- ↑ a b Calinger 1996, p. 156
- ↑ Calinger 1996, p. 125
- ↑ Calinger 1996, p. 127
- ↑ Calinger 1996, pp. 128–9
- ↑ Gekker, I. R.; Euler, A. A. «Leonhard Euler's family and descendants». Bogolyubov, Mikhaĭlov & Yushkevich 2007. [S.l.: s.n.]
- ↑ Fuss, Nicolas. «Eulogy of Euler by Fuss». Consultado em 21 de outubro de 2016
- ↑ «E212 – Institutiones calculi differentialis cum eius usu in analysi finitorum ac doctrina serierum». Dartmouth
- ↑ a b c Dunham 1999, pp. xxiv–xxv
- ↑ Euler, Leonhard. «Letters to a German Princess on Diverse Subjects of Natural Philosophy». Internet Archive, Digitzed by Google. Consultado em 15 de abril de 2013
- ↑ Frederico II da Prússia (1927). Letters of Voltaire and Frederick the Great, Letter H 7434, 25 January 1778. Richard Aldington. New York: Brentano's
- ↑ Calinger 1996, pp. 154–5
- ↑ Gindikin, S.G., Гиндикин С. Г., МЦНМО, НМУ, 2001, с. 217.
- ↑ Gekker & Euler 2007, p. 405
- ↑ «Book of Members, 1780–2010: Chapter E» (PDF). American Academy of Arts and Sciences
- ↑ A. Ya. Yakovlev (1983). Leonhard Euler. M.: Prosvesheniye
- ↑ «Eloge de M. Leonhard Euler. Par M. Fuss». Nova Acta Academia Scientarum Imperialis Petropolitanae. 1: 159–212. 1783
- ↑ Marquis de Condorcet. «Eulogy of Euler – Condorcet»
- ↑ Leonhard Euler (em inglês) no Find a Grave
- ↑ Derbyshire, John (2003). Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. Washington, D.C.: Joseph Henry Press. p. 422
- ↑ a b Boyer, Carl B.; Uta C. Merzbach (1991). A History of Mathematics. [S.l.]: John Wiley & Sons. pp. 439–445. ISBN 0-471-54397-7
- ↑ Wolfram, Stephen. «Mathematical Notation: Past and Future». Consultado em 1 de agosto de 2006
- ↑ a b Wanner, Gerhard; Harrier, Ernst (março 2005). Analysis by its history 1st ed. [S.l.]: Springer. p. 62
- ↑ Feynman, Richard (junho 1970). «Chapter 22: Algebra». The Feynman Lectures on Physics: Volume I. [S.l.: s.n.] p. 10
- ↑ Wells, David (1990). «Are these the most beautiful?». Mathematical Intelligencer. 12 (3): 37–41. doi:10.1007/BF03024015
Wells, David (1988). «Which is the most beautiful?». Mathematical Intelligencer. 10 (4): 30–31. doi:10.1007/BF03023741
See also: Peterson, Ivars. «The Mathematical Tourist». Consultado em 1 de março de 2008. Arquivado do original em 31 de março de 2007 - ↑ Albert Ingham, The Distribution of Prime Numbers (1932), Introduction, p.2 [google books]
- ↑ Dunham 1999, Ch. 3, Ch. 4
- ↑ Dunham 1999, Ch. 1, Ch. 4
- ↑ Alexanderson, Gerald (julho 2006). «Euler and Königsberg's bridges: a historical view». Bulletin of the American Mathematical Society. 43 (4): 567. doi:10.1090/S0273-0979-06-01130-X
- ↑ Cromwell, Peter R. (1999). Polyhedra. [S.l.]: Cambridge University Press. pp. 189–190. ISBN 978-0-521-66405-9
- ↑ L'Huillier, S.-A.-J. (1861). «Mémoire sur la polyèdrométrie». Annales de Mathématiques. 3: 169–189
- ↑ Calinger 1996, pp. 144–5
- ↑ Youschkevitch, A P; Biography in Dictionary of Scientific Biography (New York 1970–1990).
- ↑ Home, R. W. (1988). «Leonhard Euler's 'Anti-Newtonian' Theory of Light». Annals of Science. 45 (5): 521–533. doi:10.1080/00033798800200371
- ↑ Euler, Leonhard (1757). «Principes généraux de l'état d'équilibre d'un fluide» [General principles of the state of equilibrium of a fluid] (PDF). Académie Royale des Sciences et des Belles-Lettres de Berlin, Mémoires. 11: 217–273
- ↑ Gautschi, Walter (2008). «Leonhard Euler: His Life, the Man, and His Work» (PDF). SIAM Review. 50 (1): 3–33. Bibcode:2008SIAMR..50....3G. doi:10.1137/070702710
- ↑ Matemática do século XVIII. O decreto. op. [S.l.: s.n.] p. 35
- ↑ Baron, M. E. (maio de 1969). «A Note on The Historical Development of Logic Diagrams». The Mathematical Gazette. LIII (383): 113–125. JSTOR 3614533
- ↑ «Strategies for Reading Comprehension Venn Diagrams». Consultado em 6 de julho de 2014. Arquivado do original em 29 de abril de 2009
- ↑ «Strategies for Reading Comprehension Venn Diagrams». Arquivado do original em 29 de abril de 2009
- ↑ Euler, Leonhard (1960). Orell-Fussli, ed. «Rettung der Göttlichen Offenbahrung Gegen die Einwürfe der Freygeister». Leonhardi Euleri Opera Omnia (series 3). 12
- ↑ Williams, Rob. «Google Doodle celebrates Leonhard Euler – Swiss mathematician considered one of the greatest of all time»
Bibliografia[editar | editar código-fonte]
- Lexikon der Naturwissenschaftler, (2000), Heidelberg: Spektrum Akademischer Verlag.
- Bogolyubov, Mikhailov, and Yushkevich, (2007), Euler and Modern Science, Mathematical Association of America. ISBN 0-88385-564-X. Translated by Robert Burns.
- Bradley, Robert E., D'Antonio, Lawrence A., and C. Edward Sandifer (2007), Euler at 300: An Appreciation, Mathematical Association of America. ISBN 0-88385-565-8
- Demidov, S.S., (2005), "Treatise on the differential calculus" in Grattan-Guinness, I., ed., Landmark Writings in Western Mathematics. Elsevier: 191–98.
- Dunham, William (1999) Euler: The Master of Us All, Washington: Mathematical Association of America. ISBN 0-88385-328-0
- Dunham, William (2007), The Genius of Euler: Reflections on his Life and Work, Mathematical Association of America. ISBN 0-88385-558-5
Ver também[editar | editar código-fonte]
Ligações externas[editar | editar código-fonte]
- John J. O’Connor, Edmund F. Robertson: Leonhard Euler. In: MacTutor History of Mathematics archive.
- Leonhard Euler (em inglês) no Mathematics Genealogy Project
- Euler Archive
- «Gallica - Obras completas» (em francês)
- Leonhard Euler - Mathemathika![ligação inativa]
- Nascidos em 1707
- Mortos em 1783
- Leonhard Euler
- Membros da Academia de Ciências da Prússia
- Membros da Academia de Ciências da Rússia
- Professores da Universidade Estatal de São Petersburgo
- Teoristas dos números
- Teoristas dos grafos
- Cristãos da Suíça
- Físicos da Suíça
- Matemáticos do século XVIII
- Matemáticos da Suíça
- Calculadoras humanas
- Alunos da Universidade de Basileia
- Calvinistas
- Sepultados no Cemitério Lazarevskoe
- Naturais de Basileia


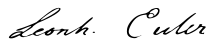










![{\displaystyle {\begin{aligned}&{\partial \rho \over \partial t}+\nabla \cdot (\rho \mathbf {u} )=0\\[1.2ex]&{\partial (\rho {\mathbf {u} }) \over \partial t}+\nabla \cdot (\mathbf {u} \otimes (\rho \mathbf {u} ))+\nabla p=\mathbf {0} \\[1.2ex]&{\partial E \over \partial t}+\nabla \cdot (\mathbf {u} (E+p))=0,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bb8b84ee55ae88472e7bf8d9d961da69479053f)

