Trigonometria
Trigonometria (do grego trigōnon "triângulo" + metron "medida") é um ramo da matemática que estuda as relações entre os comprimentos de 2 lados de um triângulo retângulo (triângulo onde um dos ângulos mede 90 graus), para diferentes valores de um dos seus ângulos agudos. A abordagem da trigonometria penetra outros campos da geometria, como o estudo de esferas usando a trigonometria esférica.[1][2]
A trigonometria tem aplicações importantes em vários ramos, tanto como na matemática pura, quanto na matemática aplicada e, consequentemente, nas ciências naturais.
Foram os babilónios os primeiros a usá-la.[3]
Círculo trigonométrico[editar | editar código-fonte]

A Trigonometria (trigono: triângulo e metria: medidas) é o ramo da Matemática que estuda a proporção, fixa, entre os comprimentos dos lados de um triângulo retângulo, para os diversos valores de um dos seus ângulos agudos. (Entre estes ângulos, os de 30º, 45º e 60º são denominados ângulos notáveis.) As proporções entre os 3 lados dos triângulos retângulos são denominadas de seno, cosseno, tangente, cotangente, entre várias outras, dependendo dos lados considerados na proporção.
Já o Círculo Trigonométrico é um recurso criado para facilitar a visualização destas proporções entre os lados dos triângulos retângulos. Ele consiste em uma circunferência orientada de raio unitário, centrada na origem dos 2 eixos de um plano cartesiano ortogonal, ou seja, um plano definido por duas retas perpendiculares entre si, ambas com o valor 0 (zero) no ponto onde elas se cortam. Existem dois sentidos de marcação dos arcos no círculo: o sentido positivo, chamado de anti-horário, que se dá a partir da origem dos arcos até o lado terminal do ângulo correspondente ao arco; e o sentido negativo, ou horário, que se dá no sentido contrário ao anterior.
Seno[editar | editar código-fonte]
Dado um triângulo retângulo, o seno de um dos seus 2 ângulos agudos é a razão entre o comprimento do cateto oposto a este ângulo e o comprimento da hipotenusa, calculada, como toda razão, pela divisão de um valor pelo outro, a referência da razão.
No círculo trigonométrico, o seno de um ângulo qualquer pode ser visualizado na projeção do seu raio (por definição igual a 1) sobre o eixo vertical.
Como o seno é esta projeção e o raio do círculo trigonométrico é igual a 1, segue que ou seja, a imagem do seno é o intervalo fechado
Cosseno[editar | editar código-fonte]
Dado um triângulo retângulo, o cosseno de um dos seus 2 ângulos agudos é a razão entre o comprimento do cateto adjacente a este ângulo e o comprimento da hipotenusa, calculada, como toda razão, pela divisão de um valor pelo outro, a referência da razão.
No círculo trigonométrico, o cosseno de um ângulo qualquer pode ser visualizado na projeção do seu raio (por definição igual a 1) sobre o eixo horizontal.
Como o cosseno é esta projeção, e o raio do círculo trigonométrico é igual a 1, segue que, ou seja, a imagem do cosseno é o intervalo fechado
Tangente[editar | editar código-fonte]
Dado um triângulo retângulo, a tangente de um dos seus 2 ângulos agudos é a razão entre o comprimento do cateto oposto a este ângulo e o comprimento do cateto adjacente a ele, calculada, como toda razão, pela divisão de um valor pelo outro, a referência da razão.
No círculo trigonométrico, o valor da tangente de um ângulo qualquer pode ser visualizado na reta vertical que tangencia este círculo no ponto em que ele corta o eixo horizontal do lado direito. Nesta reta tangente ao círculo trigonométrico, o valor da tangente trigonométrica de qualquer ângulo é representado pelo segmento que vai do ponto em que ela corta o eixo horizontal até o ponto em que ela corta a reta que contém o raio do círculo trigonométrico para o ângulo considerado. Para avaliar este valor, deve-se compará-lo com o raio do círculo trigonométrico que, por definição, é igual a 1, de preferência quando este raio se encontra sobre a parte superior do eixo ortogonal vertical. Observe que, enquanto o seno e o cosseno são sempre menores do que o raio do círculo trigonométrico e, portanto, menores do que 1, a tangente trigonométrica pode ser tanto menor quanto maior do que 1.
Relações[editar | editar código-fonte]
Dois triângulos são ditos semelhantes se um pode ser obtido pela expansão uniforme do outro. Este é o caso se, e somente se, seus ângulos correspondentes são iguais. O fato crucial sobre triângulos semelhantes é que os comprimentos de seus lados são proporcionais. Isto é, se o maior lado de um triângulo é duas vezes maior que o lado do triângulo similar, então o menor lado será também duas vezes maior que o menor lado do outro triângulo, e o comprimento do lado médio será duas vezes o valor do lado correspondente do outro triângulo. Assim, a razão do maior lado e menor lado do primeiro triângulo será a mesma razão do maior lado e o menor lado do outro triângulo.
Usando estes fatos, definem-se as funções trigonométricas, começando pelos triângulos retângulos (triângulos com um ângulo reto 90 graus ou π/2 radianos). O maior lado em um triângulo qualquer é sempre o lado oposto ao maior ângulo e devido a soma dos ângulos de um triângulo ser 180 graus ou π radianos, o maior ângulo em um triângulo retângulo é o ângulo reto. O maior lado nesse triângulo, consequentemente, é o lado oposto ao ângulo reto, chamado de hipotenusa e os demais lados são chamados de catetos.
Dois triângulos retângulos que compartilham um segundo ângulo são necessariamente similares, e a proporção (ou razão) entre o comprimento do lado oposto a e o comprimento da hipotenusa será, portanto, a mesma nos dois triângulos. Este valor será um número entre 0 e 1 que depende apenas de Este número é chamado de seno[4] de A e é escrito como Similarmente, pode-se definir :
- o cosseno de é a proporção do comprimento do cateto adjacente ao ângulo em relação ao comprimento da hipotenusa;
- a tangente trigonométrica de é a proporção do comprimento do cateto oposto ao ângulo em relação ao comprimento do cateto adjacente;
- a cotangente de é a proporção do comprimento do cateto adjacente ao ângulo em relação ao comprimento do cateto oposto - é o inverso da tangente;
- a secante trigonométrica de é a proporção do comprimento da hipotenusa em relação ao comprimento do cateto adjacente ao ângulo - é o inverso do cosseno;
- a cossecante de é a proporção do comprimento da hipotenusa em relação ao comprimento do cateto oposto ao ângulo - é o inverso do seno.
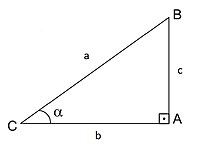
Seja o triângulo ABC, retângulo em A, têm-se, pelas definições de seno e cosseno:

Estas são as mais importantes funções trigonométricas; outras funções podem ser definidas tomando as razões dos outros lados de um triângulo retângulo, mas podem ser expressas em termos de seno e cosseno. São elas a tangente, secante, cotangente, e cossecante.
No triângulo ABC acima, a tangente de pode ser calculada através da razão entre o cateto oposto e o adjacente, como se observa em sua definição. Porém ela também pode ser obtida pela razão entre seno e cosseno, da seguinte forma:

Da mesma forma que a tangente, a cotangente de pode ser definida como uma razão entre catetos, nesse caso como a razão entre os catetos adjacente e oposto. Portanto, a cotangente pode ser expressa através da razão entre cosseno e seno como também sendo o inverso da tangente.
A secante e a cossecante ficam definidas por serem o inverso do cosseno e do seno, respectivamente. Portanto, a secante e a cossecante de podem ser expressas da seguinte forma:


Até então, as funções trigonométricas tem sido definidas por ângulos entre 0 e 90 graus (0 e π/2 radianos) apenas. Usando um círculo unitário, pode-se estendê-los para todos argumentos positivos e negativos (veja função trigonométrica).
Uma vez que as funções seno e cosseno tenham sido tabuladas (ou computadas por uma calculadora), pode-se responder virtualmente todas questões sobre triângulos arbitrários, usando a lei dos senos e a lei dos cossenos. Estas leis podem ser usadas para calcular os ângulos restantes e lados de qualquer triângulo bem como dois lados e um ângulo ou dois ângulos e um lado ou três lados conhecidos.
Alguns matemáticos acreditam que a trigonometria foi originalmente inventada para calcular relógios de sol, um tradicional exercício em antigos livros. Isto é também muito importante para a agrimensura.
Teorema de Pitágoras[editar | editar código-fonte]
O teorema de Pitágoras estabelece que "A soma do quadrado das medidas dos catetos (lados que formam o ângulo de 90°, neste caso c e b) é igual ao quadrado da medida da hipotenusa (lado oposto ao ângulo de 90°, ou a)". Assim: a² = b² + c² . Um corolário desse teorema é que se os dois catetos forem de mesmo tamanho, a hipotenusa vale o produto do cateto pela raiz quadrada de 2.
Aplicações da trigonometria[editar | editar código-fonte]
Existem diversas aplicações da trigonometria e das funções trigonométricas. Por exemplo, a técnica da triangulação é usada em astronomia para estimar a distância das estrelas próximas; em geografia para estimar distâncias entre divisas e em sistemas de navegação por satélite. As funções seno e cosseno são fundamentais para a teoria das funções periódicas, as quais descrevem as ondas sonoras e luminosas.
Campos que fazem uso da trigonometria ou funções trigonométricas incluem astronomia (especialmente para localização de posições aparentes de objetos celestes, em qual a trigonometria esférica é essencial) e portanto navegação (nos oceanos, em aviões, e no espaço), teoria musical, acústica, óptica, análise de mercado, eletrônica, teoria da probabilidade, estatística, biologia, equipamentos médicos (por exemplo, Tomografia Computadorizada e Ultrassom), farmácia, química, teoria dos números (e portanto criptologia), sismologia, meteorologia, oceanografia, muitas das ciências físicas, solos (inspeção e geodesia), arquitetura, fonética, economia, engenharia, gráficos computadorizados, cartografia, cristalografia e desenvolvimento de jogos.
Identidades trigonométricas[editar | editar código-fonte]
Algumas equações envolvendo funções trigonométricas são verdade para todos os ângulos e são conhecidas como "identidades trigonométricas". Muitas expressam relações geométricas importantes. Por exemplo, as identidades Pitagoreanas são uma expressão do Teorema de Pitágoras. Essas identidades podem ser encontradas, junto com suas demonstrações, na página Identidade Trigonométrica.
Identidades triangulares[editar | editar código-fonte]

As identidades que se seguem referem-se a um triângulo com ângulos e e lados de comprimentos e como na figura ao lado. Repare que o lado oposto ao ângulo é o de comprimento o lado oposto ao ângulo é o de comprimento e o lado oposto ao ângulo é o de comprimento
Lei dos senos[editar | editar código-fonte]
A lei dos senos[5] para um triângulo arbitrário diz:
ou equivalentemente:
Lei dos cossenos[editar | editar código-fonte]
A lei dos cossenos (também conhecida como fórmula dos cossenos) é uma extensão do teorema de Pitágoras para triângulos arbitrários:
ou equivalentemente:
o teorema de Pitágoras é um caso particular da Lei dos Cossenos, quando o cosseno de 90°é 0.
Lei das tangentes[editar | editar código-fonte]
A lei das tangentes:
Como saber o ângulo interno de um triângulo retângulo[editar | editar código-fonte]
Sendo:
em que:
- Sen(A) é comprimento do cateto oposto e
- Cos(A) é o comprimento do cateto adjacente.
A tangente inversa:
ou:
é o ângulo interno.
Referências
- ↑ Linton, 2004
- ↑ «Trigonometria». Brasil Escola. Consultado em 23 de fevereiro de 2012
- ↑ Afinal, foram os babilónios (e não gregos) os primeiros a estudar trigonometria, por Lusa, ZAP.aeiou, 25 Agosto, 2017
- ↑ Marques, Paulo. «Trigonometria, Funções». algosobre. Consultado em 24 de fevereiro de 2012
- ↑ Ribeiro, Thyago. «Lei dos Senos e dos Cossenos». Infoescola. Consultado em 25 de fevereiro de 2012
Bibliografia[editar | editar código-fonte]
- Christopher M. Linton (2004). From Eudoxus to Einstein: A History of Mathematical Astronomy . Cambridge University Press.
- Weisstein, Eric W. "Trigonometric Addition Formulas". Wolfram MathWorld.
- Christopher Mark Linton (2006) "The Trigonometric... and His Live.
- IEZZI, Gelson. Fundamentos de Matemática Elementar, trigonometria. 8 ed. São Paulo: Atual, 2004.
Ligações externas[editar | editar código-fonte]
- Oficina de trigonometriaAcessado em 24 de maio de 2008
- Ensino de Trigonometria
- «Triangle calculator» (em inglês)
- Melhoria do Ensino da Trigonometria
- Ensino de Identidades Trigonométricas


![{\displaystyle [-1,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ca7e11ebbb9225cdba1609c129e46d0ec5101a0)























![{\displaystyle {\frac {a+b}{a-b}}={\frac {\tan \left[{\tfrac {1}{2}}(A+B)\right]}{\tan \left[{\tfrac {1}{2}}(A-B)\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21e586b944db5905c0bc192c18573ecb20e63503)
![{\displaystyle {\frac {b+c}{b-c}}={\frac {\tan \left[{\tfrac {1}{2}}(B+C)\right]}{\tan \left[{\tfrac {1}{2}}(B-C)\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a56b78d0ecd84140de0ddaf336178524041bd55a)
![{\displaystyle {\frac {a+c}{a-c}}={\frac {\tan \left[{\tfrac {1}{2}}(A+C)\right]}{\tan \left[{\tfrac {1}{2}}(A-C)\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a605092f58553f5b67a63b4e22823439384b271)


