Seno

 Nota: Para outros significados, veja Seno (desambiguação).

Trigonometria

História Funções Funções inversas Aprofundamento

Referência

Lista de identidades CORDIC

Teoria euclidiana

Lei dos senos Lei dos cossenos Lei das tangentes Teorema de Pitágoras

Cálculo

Integração trigonométrica Substituição trigonométrica Integrais de funções Diferenciação trigonométrica

Gráfico da função seno, em função do ângulo em radianos

Em um círculo trigonométrico unitário, o seno do ângulo α é a medida do segmento de reta em vermelho.

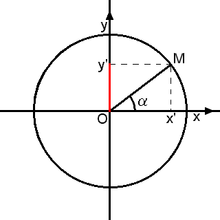
O seno é uma função trigonométrica. Dado um triângulo retângulo com um de seus ângulos internos igual a $\theta ,$ define-se $\operatorname {sen} (\theta )$ como sendo a razão entre o cateto oposto a $\theta$ e a hipotenusa deste triângulo. Ou seja:

$$\operatorname {sen} \,\theta ={\frac {\text{cateto oposto}}{\text{hipotenusa}}}$$

Exemplo: Um triângulo retângulo cuja hipotenusa é de valor 10 e seus catetos são de valores 6 e 8. O seno do ângulo oposto ao lado de valor 6 é 6/10 , ou seja, 0,6.

Definição analítica

Pode-se definir função seno pela série de Taylor:

$$\operatorname {sen} x=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}\quad {\mbox{ para todo }}x$$

Esta série possui raio de convergência infinito e as bem conhecidas propriedades da função seno podem ser demonstradas diretamente através dela.

Tal definição tem sentido tanto no conjunto dos números reais como no conjunto dos números complexos, e desta maneira pode-se definir o seno de um número complexo $z=x+iy$ como:

$$\operatorname {sen} (x+iy)=\operatorname {sen} (x)\cosh(y)+i\operatorname {senh} (y)\cos(x)$$

Onde $i$ é a unidade imaginária, $\operatorname {senh}$ é a função seno hiperbólico e $\cosh$ é a função cosseno hiperbólico.

Além disso, o seno pode ser expresso como uma soma de exponenciais complexas, devido á relação de Euler.

$e^{ix}=\cos(x)+i\operatorname {sen} (x)$

$e^{-ix}=\cos(x)-i\operatorname {sen} (x)$

$e^{ix}-e^{-ix}=2i\operatorname {sen} (x)$

$\operatorname {sen} (x)={\frac {e^{ix}-e^{-ix}}{2i}}$

A recíproca do seno é a cossecante, e sua inversa é arco seno.

Aproximações

Uma lista de aproximações, das mais simples às mais complexas.

Todas as aproximações abaixo podem ser facilmente verificadas, por exemplo, no Wolfram Alpha[1]

Aproximações Superiores

$0\leq x\leq {\frac {\pi }{2}}\rightarrow f(x)\geq sin(x)$

$f(x)=1$

$f(x)=x$

$f(x)=-{\frac {4}{\pi ^{2}}}x^{2}+{\frac {4}{\pi }}x$

$f(x)={\frac {8}{4x^{2}-4\pi x+8+\pi ^{2}}}$

$f(x)=\left({\frac {8}{\pi ^{3}}}-{\frac {4}{\pi ^{2}}}\right)x^{3}+x$

Aproximações Inferiores

$0\leq x\leq {\frac {\pi }{2}}\rightarrow f(x)\leq sin(x)$

$f(x)=0$

$f(x)={\frac {2}{\pi }}x$

$f(x)=\left({\frac {4}{\pi ^{2}}}-{\frac {2}{\pi }}\right)x^{2}+x$

$f(x)=-{\frac {1}{2}}x^{2}+{\frac {\pi }{2}}x+1-{\frac {\pi ^{2}}{8}}$

$f(x)={\frac {\pi x}{(\pi -2)x+\pi }}$

$f(x)=-{\frac {1}{6}}x^{3}+x$

$f(x)=\left({\frac {4}{\pi ^{2}}}-{\frac {16}{\pi ^{3}}}\right)x^{3}+\left({\frac {12}{\pi ^{2}}}-{\frac {4}{\pi }}\right)x^{2}+x$

História do nome "seno"

Foi através dos árabes que a trigonometria baseada na meia corda de uma circunferência, que foi apresentada pelos hindus, chegou à Europa.

Os árabes haviam traduzido textos de trigonometria do sânscrito. Os hindus tinham dado o nome de jiva à metade da corda, e os árabes a transformaram em jiba. Na língua árabe é comum escrever apenas as consoantes de uma palavra, deixando que o leitor acrescente mentalmente as vogais. Desse modo, os tradutores árabes registraram jb. Na sua tradução do árabe para o latim, Robert de Chester interpretou jb como as consoantes da palavra jaib, que significa "baía" ou "enseada", e escreveu sinus, que é o equivalente em latim. A partir daí, a jiba, ou meia corda hindu passou a ser chamada de sinus, e, em português, seno.

Ver também

• Cosseno
• Seno cardinal
• Tangente