Círculo unitário

	Trigonometria
	História ; Funções; Funções inversas ; Aprofundamento ;
	Referência
	Lista de identidades ; CORDIC
	Teoria euclidiana
	Lei dos senos ; Lei dos cossenos ; Lei das tangentes ; Teorema de Pitágoras
	Cálculo
	Integração trigonométrica ; Substituição trigonométrica ; Integrais de funções ; Diferenciação trigonométrica ; ;

Na matemática, um círculo unitário, círculo trigonométrico ou círculo goniométrico é um círculo com um raio de um. Frequentemente, especialmente em trigonometria, o círculo unitário é o círculo de raio centrado na origem do plano cartesiano, (0, 0). A generalização em dimensões superiores é a esfera unitária.

Se (x, y) é um ponto na circunferência do círculo unitário, então |x| e|y| são os comprimentos dos lados de um triângulo retângulo cuja hipotenusa tem comprimento 1. Assim, pelo Teorema de Pitágoras, x e y satisfazem a equação:

x^{2}+y^{2}=1.

Dado que x² = (−x)² para todo x, e uma vez que a reflexão de qualquer ponto no círculo unitário sobre o eixo x ou y é também sobre o círculo unitário, a equação acima é válida para todos os pontos (x, y) no círculo unitário, não apenas para aqueles no primeiro quadrante.

O interior do círculo unitário é chamado de disco unitário aberto, enquanto o interior do círculo unitário combinado com o próprio círculo unitário é chamado de disco unitário fechado.

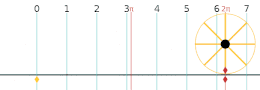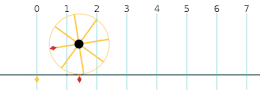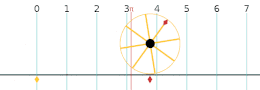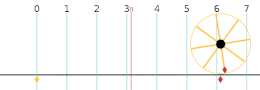
Animação do ato de desenrolamento da circunferência de um círculo unitário, um círculo de raio 1. Dado C = 2πr, a circunferência de um círculo unitário é $2π$ .

No plano complexo[editar | editar código-fonte]

O círculo unitário pode ser considerado como a unidade dos números complexos, ou seja, o conjunto de números complexos z da forma

z=\,\mathrm {e} ^{it}\,=\cos(t)+i\sin(t)\,

para todo t. Esta relação é a Fórmula de Euler. Em Mecânica quântica, isto é referido como o fator de fase.

Funções trigonométricas no círculo unitário[editar | editar código-fonte]

As funções trigonométricas de seno, cosseno e tangente do ângulo θ podem ser definidas no círculo unitário da seguinte forma: Se (x, y) é um ponto no círculo unitário, e, se o raio a partir da origem (0, 0) para (x, y) faz um ângulo t em relação ao eixo x positivo (sentido anti-horário é positivo), então^[1]

{\begin{array}{rcl}x&=&\cos \theta \\y&=&\sin \theta \end{array}}

A partir do círculo unitário é possível deduzir várias identidades trigonométricas.

A equação x² + y² = 1 dá a relação

\cos ^{2}(\theta )+\sin ^{2}(\theta )=1.\,\!

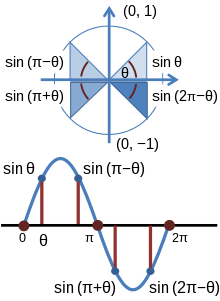
O círculo unitário também demonstra que seno e cosseno são funções periódicas, com as identidades

\cos \theta =\cos(2\pi k+\theta )\,\!

\sin \theta =\sin(2\pi k+\theta )\,\!

para qualquer número inteiro k.

Triângulos construídos no círculo unitário podem também ser usados para ilustrar a periodicidade das funções trigonométricas. Primeiro, constrói-se um raio OA a partir da origem para um ponto P(x₁,y₁) sobre o círculo unitário de tal modo que um ângulo t with 0 < t < π/2 é formado sobre o lado positivo do eixo x. Agora, considere um ponto Q(x₁,0) e um segmento de linha PQ $\perp$ OQ. O resultado é um triângulo retângulo ΔOPQ com ∠QOP = t. Porque PQ tem comprimento y₁, OQ comprimento x₁, e OA um comprimento 1, sen (t) = y₁ e cos (t) = x₁. Estabelecidas essas equivalências, pegue outro raio OR a partir da origem para um ponto R(−x₁,y₁) no círculo de tal modo que o mesmo ângulo t é formado com o lado negativo do eixo x. Agora, considere um ponto S(−x₁,0) e una os segmentos RS $\perp$ OS. O resultado é um triângulo retângulo com ΔORS ∠SOR = t. Pode, portanto, ser visto que, por causa ∠ROQ = π-t, em que R é (cos (π-t), sen (π-t)) da mesma maneira que P é a (cos (t), sen (t )). A conclusão é que, uma vez que (X1, Y1) é o mesmo que (cos (π-t), sen (π-t)) e (x1, y1) é o mesmo que (cos (t) sen (t, )), é verdade que sen (t) = sin (π-t) e -cos (t) = cos (π-t). Pode-se inferir de uma maneira semelhante que tan (π-t) = -tan (t), uma vez que tan (t) = y1 / x1 e tan (π-t) = y1 / (- x1). Uma simples demonstração do acima pode ser visto na igualdade seno(π/4) = seno (3π / 4) = ${\frac {\sqrt {2}}{2}}$