Malha plana por polígonos regulares

Malhas Planas por polígonos regulares vêm sendo usadas desde a antiguidade sem ser, no entanto, classificadas ou ter um estudo sistematizado. O primeiro tratamento matemático do assunto foi o de Kepler em seu livro Harmonices Mundi, que generalizou o conceito dos sólidos de arquimedes para o plano Euclidiano. Malhas por polígonos regulares cobrem o plano utilizando apenas polígonos regulares em arranjos em torno de um vértice.

Malhas planas regulares

De acordo com Grünbaum and Shephard (section 1.3), uma malha plana ocorre quando seu grupo de simetria age transitivamente em suas "bandeiras", onde uma bandeira é uma tripla que consiste de vértice, arestas e polígonos (ou ladrilho) mutuamente incidentes. Isso significa que para cada par de bandeiras há uma operação de simetria que mapeia a primeira bandeira à segunda. Uma malha plana é dita regular quando consiste de um único tipo de polígono regular. A criação de malhas regulares é possível através da utilização de seis triângulos equiláteros, quatro quadrados ou três hexágonos regulares por vértice, produzindo dessa forma os três tipos de malha plana regulares.

36 Malha plana Triangular

44 Malha plana Quadrada

63 Malha Plana Hexagonal

Malhas Arquimedianas, uniformes ou semi-regulares

Transitividade do vértice significa que para cada par de vértices há uma operação de mapeamento simétrica do primeiro vértice para com o segundo.

Se o requerimento da transitividade da bandeira é reduzido para uma transitividade do vértice, quando a condição aresta-aresta da malha for mantida, haverá oito possíveis malhas adicionais, conhecidos como malhas "Arquimedianas", "uniformes" ou malhas planas "semi-regulares" exibidas abaixo. Note que há duas formas de imagens espelhadas da malha 3⁴.6, ambas as quais são mostradas na tabela a seguir seguidas das outras malhas planas regulares e semi-regulares.

34.6 Snub hexagonal tiling	34.6 Snub hexagonal tiling reflection	3.6.3.6 Trihexagonal tiling
33.42 Elongated triangular tiling	32.4.3.4 Snub square tiling	3.4.6.4 Rhombitrihexagonal tiling
4.82 Truncated square tiling	3.122 Truncated hexagonal tiling	4.6.12 Truncated trihexagonal tiling

Grünbaum e Shephard distinguiram a descrição dessas malhas como malhas “Arquimedianas” referindo-se somente a propriedade local do arranjo das malhas ao redor de cada vértice, e como “uniforme” referindo-se a propriedade global da transitividade do vértice. Embora dessa forma se possa obter o conjunto de malhas no plano, em outros espaços existem outros tipos de malha que são “Arquimedianas” mas não são “uniformes”.

Combinações de polígonos regulares que podem se encontrar em um vértice

Os ângulos internos dos polígonos que se encontram em um vértice devem somar 360º. Um polígono regular de n lados tem ângulos internos de $\left(1-{\frac {2}{n}}\right)180$ graus. Há 17 combinações de polígonos regulares cuja soma dos ângulos internos é 360º, cada um sendo referido como “espécies” do vértice; Em quatro casos há duas ordens cíclicas distintas dos polígonos, originando 21 “tipos” de vértice. Somente 11 deles podem ocorrer em uma malha plana uniforme de polígonos regulares. Em particular, se três polígonos se encontram em um vértice e um deles possui um número ímpar de lados, os outros dois polígonos são necessariamente do mesmo tamanho. Se não fossem, eles teriam que se alternar em volta do primeiro polígono, o que é impossível se o número de lados for ímpar.

Com 3 polígonos em um vértice:

• 3.7.42 (não pode existir em nenhum tipo de malha plana por polígonos regulares)
• 3.8.24 (não pode existir em nenhum tipo de malha plana por polígonos regulares)
• 3.9.18 (não pode existir em nenhum tipo de malha plana por polígonos regulares)
• 3.10.15 (não pode existir em nenhum tipo de malha plana por polígonos regulares)
• 3.12² - semi-regular, truncated hexagonal tiling
• 4.5.20 (não pode existir em nenhum tipo de malha plana por polígonos regulares)
• 4.6.12 - semi-regular, truncated trihexagonal tiling
• 4.8² - semi-regular, truncated square tiling
• 5².10 (não pode existir em nenhum tipo de malha plana por polígonos regulares)
• 6³ - regular, hexagonal tiling

Abaixo os diagramas desses vértices:

• 
  3.7.42
• 
  3.8.24
• 
  3.9.18
• 
  3.10.15
• 
  3.12.12
• 
  4.5.20
• 
  4.6.12
• 
  4.8.8
• 
  5.5.10
• 
  6.6.6

Com 4 polígonos em um vértice:

• 3².4.12 - não uniforme. Há dois tipos diferentes de vértice: 3².4.12 e 3⁶
• 3.4.3.12 - não uniforme. Há dois tipos diferentes de vértice: 3.4.3.12 e 3.3.4.3.4
• 3².6² - não uniforme. Ocorre em dois padrões de vértice: 3².6²/3⁶ e 3².6²/3.6.3.6.
• 3.6.3.6 - semi-regular, trihexagonal tiling
• 4⁴ - regular, square tiling
• 3.4².6 - não uniforme. Tem vértices 3.4².6 e 3.6.3.6.
• 3.4.6.4 - semi-regular, rhombitrihexagonal tiling

Abaixo os diagramas desses vértices:

• 
  3.3.4.12
• 
  3.4.3.12
• 
  3.3.6.6
• 
  3.6.3.6
• 
  4.4.4.4
• 
  3.4.4.6
• 
  3.4.6.4

Com 5 polígonos em um vértice:

• 3⁴.6 - semi-regular, Snub hexagonal tiling, aparecendo em duas entianomorphic formas. Os vértices das duas formas são o mesmo, mas as malhas planas resultantes são diferentes.
• 3³.4² - semi-regular, Elongated triangular tiling
• 3².4.3.4 - semi-regular, Snub square tiling

Abaixo os diagramas desses vértices:

• 
  3.3.3.3.6
• 
  3.3.3.4.4
• 
  3.3.4.3.4

Com 6 polígonos em um vértice:

• 3⁶ - regular, Triangular tiling

Abaixo o diagrama desse vértice:

• 
  3.3.3.3.3.3

Outras malhas planas aresta-aresta

Um número variado de malhas planas aresta-aresta não uniformes (chamadas de demi-regulares)por polígonos regulares também podem ser desenhadas. Aqui estão quatro exemplos:

32.62 and 36	32.62 and 3.6.3.6
32.4.12 and 36	3.42.6 and 3.6.3.6

Essas malhas planas podem ser classificadas de acordo com o número de vértices, arestas ou malhas. Se houver $n$ órbitas dos vértices, a malha plana é conhecida como $n$-uniform ou $n$-isogonal. Se houver $n$ órbitas de malha, recebem o nome de $n$-isohedral. Se houver $n$ órbitas de arestas, são conhecidas como $n$-isotoxal. Os exemplos acima são 4 das 20 malhas planas uniformes.

Malhas planas que não são aresta-aresta

Polígonos regulares também podem formar malhas planas que não são aresta-aresta. Essas malhas podem também ser uniformes ou não, dependendo da transitividade do vértice. Existem 8 famílias dessas malhas uniformes, cada família tendo um parâmetro cujo valor real determina se há sobreposição entre os lados adjacentes da malha ou se há relação entre os comprimentos das arestas em diferentes malhas.

Malha plana hiperbólica

Essas malhas são relatadas devido a polígonos regulares ou semi-regulares em outra dimensão que não a IR². Os polígonos semi-regulares dessa ordem são construídos a partir de faces regulares de um polígono em 2ª dimensão, mas seus ângulos devem somar menos de 360º. Polígonos regulares em geometria hiperbólica possui ângulos menores do que eles possuem em 2ª dimensão. Em ambos os casos, o arranjo dos polígonos em cada vértice não significa que o polígono da dimensão superior possui transitividade nesse vértice.

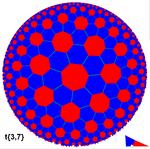
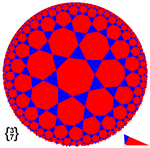
Algumas malhas regulares em plano hiperbólico:

Referências

• Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. [S.l.]: W. H. Freeman and Company. ISBN 0-7167-1193-1  !CS1 manut: Nomes múltiplos: lista de autores (link)
• D. Chavey (1989). «Tilings by Regular Polygons—II: A Catalog of Tilings». Computers & Mathematics with Applications. 17: 147–165. doi:10.1016/0898-1221(89)90156-9 
• D. M. Y. Sommerville, An Introduction to the Geometry of n Dimensions. New York, E. P. Dutton, 1930. 196 pp. (Dover Publications edition, 1958) Chapter X: The Regular Polytopes

Ligações externas

Euclides e malhas planas gerais:

• Dutch, Steve. «Uniform Tilings». Consultado em 9 de setembro de 2006. Arquivado do original em 9 de setembro de 2006 
• Mitchell, K. «Semi-Regular Tilings». Consultado em 9 de setembro de 2006 
• Weisstein, Eric W. «Semiregular tessellation» (em inglês). MathWorld 
  • Weisstein, Eric W. «Demiregular tessellation» (em inglês). MathWorld 

Malhas hiperbólicas:

• Eppstein, David. «The Geometry Junkyard: Hyperbolic Tiling». Consultado em 9 de setembro de 2006 

• Hatch, Don. «Hyperbolic Planar Tessellations». Consultado em 9 de setembro de 2006 

• Joyce, David. «Hyperbolic Tessellations». Consultado em 9 de setembro de 2006