Paradoxo do quadrado perdido

O enigma do quadrado perdido.

O enigma em animação.

Sobreposição dos dois pseudo-triângulos

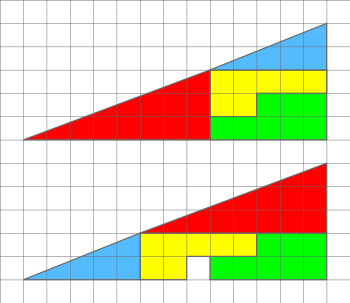
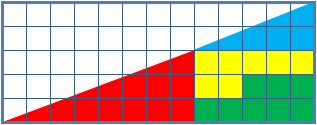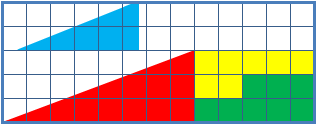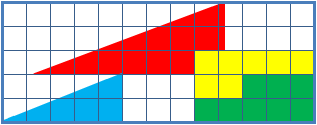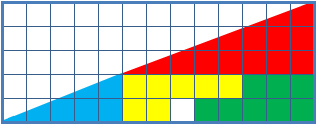
O paradoxo do quadrado perdido é um enigma resultado de uma ilusão de óptica, em que são vistos dois triângulos, formados pelas mesmas peças, onde porém um triângulo aparenta ter um pequeno quadrado a menos do que o outro. A suposta hipotenusa de cada figura não é reta (apesar de parecer).

De acordo com Martin Gardner, esse enigma foi elaborado em 1953 pelo mágico amador Paul Curry, de Nova Iorque. O enigma do quadrado perdido é por isso também chamado de paradoxo de Curry (embora exista o paradoxo de Curry de teoria ingênua dos conjuntos). O princípio por trás desse tipo de paradoxo é conhecido desde pelo menos 1860.

Explicação

Descrição

Os dois triângulos formados por peças coloridas parecem ter a mesma área de $13\cdot5\cdot\frac{1}{2}$.

As peças de cada triângulo formado por peças:

• Um triângulo (aqui azul) com área de
  $5 \cdot 2 \cdot \frac{1}{2}\ \mathrm{cm^2}\ =\ 5\ \mathrm{cm^2}$
• Outro triângulo (aqui vermelho) com área de
  $8 \cdot 3 \cdot \frac{1}{2}\ \mathrm{cm^2}\ =\ 12\ \mathrm{cm^2}$
• Duas outras figuras (aqui, uma amarela e a outra verde), que juntas tem o tamanho de um retângulo
  $5\cdot 3\ \mathrm{cm^2}\ =\ 15\ \mathrm{cm^2}$
  área que é a soma de
  $1 \cdot 5\ \mathrm{cm^2}+1 \cdot 2\ \mathrm{cm^2}\ =\ 7\ \mathrm{cm^2}$ da figura amarela
  $1 \cdot 5\ \mathrm{cm^2}+1 \cdot 3\ \mathrm{cm^2}\ =\ 8\ \mathrm{cm^2}$ da figura verde

Embora ambos sejam visualmente triângulos de mesmo tamanho com sub-áreas idênticas, no segundo triângulo há um quadrado de área $1 \times 1\ \mathrm{cm^2}$ restando.

Solução

A soma das áreas das peças resulta em uma área de $5\ \mathrm{cm^2}+12\ \mathrm{cm^2}+7\ \mathrm{cm^2}+8\ \mathrm{cm^2}\ = \ 32\ \mathrm{cm^2}$

No entanto, um triângulo com lados 13 e 5 deve ter uma área de $13\cdot5\cdot\frac{1}{2}\ \mathrm{cm^2}\ = \ 32,5\mathrm{cm^2}$.
Assim, está dada a prova matemática de que o dado triângulo não pode ser formado por essas peças.

O paradoxo se deve a diferença entre os ângulos dos triângulos azul e vermelho (eles não são triângulos similares). Portanto, a hipotenusa não é uma reta. Matematicamente, isso pode ser provado da seguinte maneira:

• Triângulo azul:
  $\arctan\left(\frac{2}{5}\right)=\arctan\left(0,4\right)=21,8\,^{\circ}$
• Triângulo vermelho:
  $\arctan\left(\frac{3}{8}\right)=\arctan\left(0,375\right)=20,56\,^{\circ}$
• Ângulo de um triângulo com catetos 13 e 5:
  $\arctan\left(\frac{5}{13}\right)=\arctan\left(0,385\right)=21,04\,^{\circ}$

Disso percebe-se que o lado de cima não é uma linha reta. Portanto, a figura composta não é realmente um triângulo, mas sim um quadrilátero.

Seqüência de Fibonacci

Figuras enganosas como essa podem também ser formadas com outras proporções. As dimensões inteiras dos lados das figuras de cima: 2, 3, 5, 8 e 13; são cinco números consecutivos da sequência de Fibonacci. Muitas outras figuras, que apresentam o mesmo fenômeno, também são feitas com outros números consecutivos na sequência de Fibonacci.

Ligações externas

• Curry's Paradox: How Is It Possible? (em inglês)