Peso
O peso de um objeto é a força gravitacional sofrida por este objeto em virtude da atração gravitacional nele exercida por um outro corpo com massa.[1]

Em senso comum, o peso é associado à força que um objeto com massa exerce sobre outro corpo pela atração gravitacional, contudo em termos científicos a definição é simétrica: o corpo que exerce a força também está sujeito por uma força associada ao outro objeto, sendo em verdade este peso exatamente igual em módulo ao peso do próprio objeto em virtude da terceira lei de Newton.
Leigos sobre o assunto geralmente confundem os conceitos de peso e massa. Contudo ressalva-se que peso e massa são grandezas completamente distintas, apesar de relacionadas. Ao passo que massa é uma grandeza escalar,[2] peso é uma grandeza vetorial.
Representação matemática[editar | editar código-fonte]
O peso é uma grandeza vetorial, apresentando intensidade, direção e sentido. A direção é a linha que passa pelos centros do objeto e do corpo com massa e o sentido é o que aponta para o centro de massa do corpo responsável pela atração. A unidade usada é o newton (N).
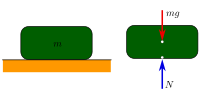
É expresso por:[1]
.
Nessa expressão g é a aceleração gravitacional no ponto do espaço onde encontra-se o objeto de massa m.[1] A aceleração g pode ser calculada mediante a expressão:[3]
onde M é a massa do corpo responsável pela aceleração e R é a distância entre o ponto em consideração — necessariamente externo ao corpo neste caso — e o centro de massa deste corpo [nota 1]
Para distâncias próximas à superfície da Terra, os cálculos fornecem uma valor próximo: . Para um corpo de massa 1 Kg, o seu peso é de 9,82 N.
Peso em outros corpos celestes[editar | editar código-fonte]
Devido às diferentes massas e raios dos planetas do sistema solar, o peso de um mesmo objeto de massa m quando próximo às suas superfícies será diferente para cada um deles. Segue-se uma tabela contendo o valor aproximado da aceleração gravitacional na superfície de cada um destes planetas:
| Corpo celeste | Em relação à Terra | m/s² |
|---|---|---|
| Sol | 27,90 | 274,1 |
| Mercúrio | 0,3770[4] | 3,703 |
| Vênus | 0,9032[4] | 8,872 |
| Terra | 1 (por definição)[4] | 9,81 |
| Lua | 0,1655 | 1,625 |
| Marte | 0,3895[4] | 3,728 |
| Júpiter | 2,640[4] | 25,93 |
| Saturno | 1,139 | 11,19 |
| Urano | 0,917 | 9,01 |
| Netuno | 1,148[4] | 11,28 |
Pela tabela, a força da gravidade na Lua é seis vezes menor do que na Terra. Assim um corpo de 60 Kg que na Terra tem cerca de 600 N de peso, na Lua terá cerca de 100 N.
O peso dos corpos na Terra[editar | editar código-fonte]
Devido à irregularidade na forma do planeta e à quebra de simetria produzida pela rotação do mesmo, o peso de um corpo sofre pequenas variações ao longo da superfície do planeta, sendo a rigor dependente da posição que o mesmo ocupa no globo. As variáveis que interferem são basicamente: a distância ao centro de massa terrestre e a força centrípeta a ele associada em função deste acompanhar o movimento de rotação do planeta em seu próprio eixo.
O peso de um corpo na Terra:
- Aumenta do equador aos pólos. Os principais motivos são: formato de geoide que o planeta apresenta, sendo ligeiramente achatado nos pólos e dilatado no equador, implicando menor distância do objeto ao centro da Terra; a resultante centrípeta é menor em latitudes maiores, visto que o raio da trajetória circular que descreve, determinado de forma perpendicular ao eixo de rotação da terra e não em relação ao centro da Terra, diminui gradualmente, embora a velocidade angular do movimento permaneça a mesma. Nas regiões de latitude 90º a resultante centrípeta é considerada nula;
- Diminui quando a altitude do lugar aumenta,[1] visto que R (distância ao centro de massa terrestre) aumenta.
Notas
- ↑ Esta equação decorre da aplicação da Lei de Gauss à situação, e subentende-se portanto uma simetria esférica para o corpo responsável pela atração.
Referências
- ↑ a b c d Clark, John (1996). A Física. [S.l.]: Círculo de Leitores. p. 38. ISBN 972-42-1322-6
- ↑ Clark, John (1996). A Física. [S.l.]: Círculo de Leitores. p. 34. ISBN 972-42-1322-6
- ↑ Clark, John (1996). A Física. [S.l.]: Círculo de Leitores. p. 29. ISBN 972-42-1322-6
- ↑ a b c d e f Cattermole, Peter (1996). A Terra e o Sistema Solar. [S.l.]: Círculo de Leitores. p. 146. ISBN 972-42-1471-0
Ver também[editar | editar código-fonte]



