Rede neural artificial

Em ciência da computação e campos relacionados, redes neurais artificiais (português brasileiro) ou redes neuronais artificiais (português europeu)[1] (RNAs) são modelos computacionais inspirados pelo sistema nervoso central de um animal (em particular o cérebro) que são capazes de realizar o aprendizado de máquina bem como o reconhecimento de padrões. Redes neurais artificiais geralmente são apresentadas como sistemas de "neurônios interconectados, que podem computar valores de entradas", simulando o comportamento de redes neurais biológicas.
Por exemplo, uma rede neural para o reconhecimento de escrita manual é definida por um conjunto de neurônios de entrada que podem ser ativados pelos pixels de uma imagem de entrada. Os dados adquiridos por essa ativação dos neurônios são então repassados, ponderados e transformados por uma função[2] determinada pelo designer da rede, a outros neurônios. Este processo é repetido até que, finalmente, um neurônio de saída é ativado. Isso determina que caractere foi lido.[3]
Assim como outros métodos de aprendizado de máquina, sistemas que aprendem a partir dos dados, redes neurais têm sido usadas para resolver uma grande variedade de tarefas que são difíceis de resolver utilizando programação baseada em regras comuns, incluindo visão computacional e reconhecimento de voz.
Exemplos
[editar | editar código-fonte]A inspiração original para essa técnica advém do exame das estruturas do cérebro, em particular do exame de neurônios. A propriedade mais importante das redes neurais é a habilidade de interagir com seu ambiente em busca de reconhecer padrões que podem solucionar problemas dos mais fáceis aos mais complexos consequentemente melhorando seu desempenho. Isso é feito através de um processo iterativo de ajustes aplicado aos seus pesos, o treino.
A aprendizagem ocorre quando a rede neural atinge uma solução generalizada para uma classe de problemas.
Denomina-se algoritmo de aprendizagem a um conjunto de regras bem definidas para a solução de um problema de aprendizagem. Outro fator importante é a maneira pela qual uma rede neural se relaciona com o ambiente. Nesse contexto existem os seguintes paradigmas de aprendizagem:
Aprendizagem Supervisionada, quando é utilizado um agente externo que indica à rede a resposta desejada para o padrão de entrada, Aprendizagem Não Supervisionada (auto-organização), quando não existe uma agente externo indicando a resposta desejada para os padrões de entrada, e Aprendizagem por Reforço, quando um crítico externo avalia a resposta fornecida pela rede.
Aplicações
[editar | editar código-fonte]Reconhecimento Automático de Alvos; Reconhecimento de Caracteres; Robótica; Diagnóstico Médico; Sensoriamento Remoto; Processamento de Voz; Biometria; Análise de dados (Data Mining), incluindo para análise de imagem de sistemas quânticos.[4] Cientistas russos substituíram especialistas em caminhada quântica por inteligência artificial, treinando a máquina para reconhecer redes e dizer se um determinado sistema trará vantagens quânticas.[5] Isso indica as redes que são boas candidatas para a construção de um computador quântico.[2]
Aplicações em reconhecimento de padrões; Análise de disfluência da fala - Junto ao Departamento de Fisioterapia, Fonoaudiologia e Terapia Ocupacional da Faculdade de Medicina da USP; Tratamento corretivo do aparelho buco-maxilar - Junto ao Departamento de Informática Médica, Faculdade de Medicina da USP; Predição da Doença de Alzheimer - Junto ao Departamento de Informática Médica, Faculdade de Medicina da USP; Reconhecimento de câncer – Câncer de mamas PPEP e Disciplina e Informática Médica, Faculdade de Medicina da USP; Análise do Planejamento Urbano da Cidade de São Paulo; Aplicações em Tomada de Decisão em Engenharia de Produção; Mercado Financeiro.[6]
História
[editar | editar código-fonte]As primeiras informações sobre neurocomputação surgiram em 1943, em artigos do neuroanatomista e psiquiatra Warren McCulloch, do Instituto Tecnológico de Massachusetts, e do matemático Walter Pitts, da Universidade de Illinois. Os autores fizeram uma analogia entre células nervosas vivas e o processo eletrônico, em um trabalho publicado sobre "neurônios formais"; simulando o comportamento do neurônio natural, no qual o neurônio possuía apenas uma saída, que era uma função da soma de valor de suas diversas entradas. O trabalho consistia num modelo de resistores variáveis e amplificadores, representando conexões sinápticas de um neurônio biológico.
Década de 1940
[editar | editar código-fonte]Possivelmente uma das publicações mais significativas, formulada por von Neumann, foi The General and Logical Theory of Automata, no final da década de 1940.
Talvez a mais remota influência (no início do século XIX), foi a do "Pato de Vaucanson", um autômato em forma de pato com centenas de peças e que além de grasnar, comia, bebia, digeria e nadava. Não esquecendo de mencionar também a máquina de Turing (1936). O resultado do autômato de Turing influenciou von Neumann, e o levou a perceber que os seres vivos estavam de fato entre as máquinas que a máquina de Turing poderia emular. Na sua obra, arquitetura de von Neumann, ele fez uma analogia entre os órgãos e as partes de um computador, entre portas lógicas, circuitos e neurônios.[7]
O livro Cybernetics de Wiener publicado em 1948 descreve alguns conceitos sobre controle, comunicação e processamento estatístico de sinais. Em 1961 foi adicionado na segunda edição do livro material sobre aprendizagem e auto-organização. Em ambas as edições desse livro o Capítulo 2 traz o compreendimento do significado físico da mecânica estatística no contexto desse assunto segundo Wiener, mas quem conseguiu terminar a ligação entre a mecânica estatística e os sistemas de aprendizagem foi Hopfield mais de 30 anos depois.[8]
Em meados de 1948, o polonês Stanilaw Jaśkowskipor, discípulo de Łukasiewicz, publicou estudos sobre cálculo proposicional paraconsistente. Em meados da década de 1950, Jaśkowski e o brasileiro matemático lógico Newton Carneiro Affonso da Costa propuseram a contradição na estrutura lógica e ficaram conhecidos como os fundadores da Paraconsistent Logic. Newton Carneiro Affonso da Costa propôs, em 1954, predicados, lógicas de ordem superior (teoria de conjuntos).[9] A Lógica Paraconsistente faz parte das chamadas lógicas não clássicas (ABE, 2011), pois contém disposições contrárias a alguns dos princípios básicos da Lógica Aristotélica, como o princípio da contradição. Essa nova lógica surgiu com o reconhecimento pela comunidade científica (ABE, 2011) do lógico polonês Jan Łukasiewicz Lvov, nascido em 1878, e do filósofo russo Nicolai Alexandrovich Vasilév, nascido em 1910, considerados predecessores da Lógica Paraconsistente, batizada inclusive como Lógica Imaginária.[10]
Em 1949 Hebb introduziu a capacidade de aprender através de seu livro "The Organization of Behavior". Hebb descreveu um sistema de aprendizado por correlação dos neurônios que acabou dando origem à Regra de Aprendizagem de Hebb e essa teoria é comumente evocada para explicar alguns tipos de aprendizagem associativos no qual a ativação simultânea de células leva a um crescimento pronunciado na força sináptica. Tal aprendizado é conhecido como aprendizagem hebbiana.[11]
Década de 1950
[editar | editar código-fonte]Em 1951, foi construído o primeiro neuro computador denominado Snark, por Mavin Minsky. O Snark operava com sucesso a partir de um ponto de partida técnico, ajustando seus pesos automaticamente, entretanto, ele nunca executou qualquer função de processamento de informação interessante, mas serviu de inspiração para as ideias de estruturas que o sucederam.
O livro de Ashby (Design for a Brain: The Origin of Adaptive Behavior) que foi publicado em 1952 trata do conhecimento básico de que o comportamento adaptativo não nasce com o indivíduo, mas sim é aprendido, e que através da aprendizagem o animal (sistema) normalmente muda seu comportamento para melhor. São enfatizados neste livro os aspectos dinâmicos do organismo vivo como uma máquina e o conceito correlacionado de estabilidade.
Gabor, um dos pioneiros da teoria da comunicação e o inventor da holografia, propôs em 1954 a ideia de um filtro adaptativo não linear. Com a ajuda de colaboradores, Gabor construiu uma máquina que alimentada com amostras de um processo estocástico, mais a função-alvo que a máquina deveria produzir, realizava a aprendizagem.
Em 1954-1955, Cragg e Tamperley observaram que os átomos em uma rede têm seus spins apontando "para cima" ou "para baixo", assim como os neurônios podem ser "disparados" (ativados) ou "não disparados" (quiescentes).[12]
Em 1956 no Darthmouth College nasceram os dois paradigmas da Inteligência Artificial, a simbólica e o conexionista. A Inteligência Artificial Simbólica tenta simular o comportamento inteligente humano desconsiderando os mecanismos responsáveis por tal. Já a Inteligência Artificial Conexionista acredita que construíndo-se um sistema que simule a estrutura do cérebro, este sistema apresentará inteligência, ou seja, será capaz de aprender, assimilar, errar e aprender com seus erros. O livro de Hebb tem sido uma fonte de inspiração para o desenvolvimento de modelos computacionais de sistema adaptativos e de aprendizagem. O artigo de Rochester, Holland, Haibt e Duda (1956) talvez seja a primeira tentativa de usar simulação computacional para testar uma teoria neural bem-formulada com base no postulado de aprendizagem de Hebb (que a eficiência de uma sinapse variável entre dois neurônios é aumentada pela ativação repetida de um neurônio causada pelo outro neurônio). Naquele mesmo ano Uttley (1956) demonstrou que uma rede neural com sinapses modificáveis pode aprender a classificar conjuntos simples de padrões binários em classes correspondentes.
Em 1957 Rosenblatt inicia testes simulados em um computador IBM 704 no Laboratório da Aeronáutica de Cornell. Pelo estudo de redes neurais, como a Perceptron, Rosenblatt esperava que as leis fundamentais da organização que são comuns a todos os sistemas de informação de movimentação, máquinas e homens incluídos, pudesse eventualmente ser compreendida.
Em 1958, Frank Rosenblatt criou o Perceptron, um modelo cognitivo que consistia de unidades sensoriais conectadas a uma única camada de neurônios de Warren McCulloch e Pitts, capaz de aprender tudo o que pudesse representar. Rosenblatt demonstrou que, se fossem acrescidas sinapses ajustáveis, as redes neurais de Warren McCulloch e Pitts poderiam ser treinadas para classificar padrões em classes linearmente separáveis, convergindo em um número limitado de passos.[13]
Eficiência de transmissão (peso) ajustável; esta envia a resposta (saídas) para a terceira camada.
O intuito de Rosenblatt era projetar RNAs que fossem capazes de fazer descobertas interessantes sem a necessidade de regras, o que, aliás, continua sendo alvo dos pesquisadores.[14]
Década de 1960
[editar | editar código-fonte]No início da década de 1960, Widrow e Hoff publicam um artigo no qual especificam um neurônio artificial baseado no modelo de McCulloch e Pitts, denominado ADALINE. Conforme,[13] a importância desse modelo está associada à regra de aprendizagem proposta, a regra Delta. A combinação de uma série de ADELINEs é chamada de MADALINE (Multiple Adaline) é uma de duas camadas de rede neural com um conjunto de ADALINEs. Widrow também fundou a primeira companhia de hardware de neurocomputadores e componentes.
Em 1967, Cowan caracterizou o disparo "sigmóide" e a condição de disparo suave para um neurônio baseando-se na função logística.
Em 1967-1968, Grossberg envolvendo equações não-lineares de diferenças/diferenciais introduziu o modelo aditivo de um neurônio e como base para a memória de curto prazo explorou o uso do modelo.[12]
A publicação de Perceptrons de Minsky e Papert, em 1969, expôs as limitações do modelo de Rosenblatt, provando que tais redes não são capazes de resolver uma ampla classe de problemas devido às restrições de representação.[13][15] O impacto desta publicação foi devastador, praticamente desaparecendo o interesse em redes neurais artificiais nos anos seguintes, somente poucos pesquisadores como Malsburg, Grossberg, Kohonen e Anderson permaneceram concentrando suas atividades na abordagem conexionista.
Década de 1970
[editar | editar código-fonte]Nos anos 70, não ocorreram grandes progressos nos estudos de redes neurais devido um entusiasmo exagerado de muitos pesquisadores, que passaram a publicar mais e mais artigos e livros que faziam uma previsão pouco confiável para a época, sobre máquinas tão poderosas quanto o cérebro humano que surgiriam em um curto espaço de tempo. Isto tirou quase toda a credibilidade dos estudos desta área e causou grandes aborrecimentos aos técnicos de outras áreas.
Dentre os poucos pesquisadores que continuaram trabalhando na área, destacam-se:
- Igor Aleksander, Inglaterra: redes sem pesos;
- Kunihiko Fukushima, Japão: cognitron e neocognitron;
- Steven Grossberg, Estados Unidos: sistemas auto-adaptativos;
- Teuvo Kohonen, Finlândia: memórias associativas e auto-organizadas.[14]
No ano de 1970 a Universidade de Michigan foi palco para as pesquisas de vida artificial, J. Holland foi o primeiro pesquisador a conseguir o título de PhD em Ciência da Computação. Ele e T. Toffoli foram atraidos pela ideia de comportamento adaptativo onde envolvia biologia, computadores e informação, se tornaram associados em algoritmos genéricos e autômatos celulares, respectivamente. Toffoli sempre se preocupou em criar a conexão do mundo físico com o autômato.
Em 1972 foi introduzido de forma independente por Amari o modelo aditivo de um neurônio para estudar o comportamento dinâmico de elementos semelhantes a neurônios conectados aleatoriamente.
Ainda em 1972, Wilson e Cowan derivaram equações diferenciais não-lineares acopladas correspondentes à dinâmica de populações localizadas no espaço, contendo neurônios tanto excitadores como inibitórios.
- 1974: WERBOS lançou bases para o algoritmo de retropropagação (backpropagation).
Em 1975, Little e Shaw descreveram e usaram o modelo probabilístico de um neurônio, disparando ou não um potencial de ação, para desenvolver uma teoria da memória de curto prazo.
Em 1977, Andereson, Silverstein, Ritz e Jones, sugeriram o modelo do estado cerebral em uma caixa (BSB, brain-state-in-a-box), compondo-se de uma rede associativa simples acoplada a uma dinâmica não-linear.[12]
Década de 1980
[editar | editar código-fonte]A partir dos anos 80, com o avanço da tecnologia e o fracasso da escola simbolista na solução de determinados tipos de problemas, as redes neurais artificiais passaram a atrair substancial atenção novamente, as pesquisas na área foram retomadas com força. A nova explosão de interesse pelas redes neurais artificiais na comunidade científica foi impulsionada, principalmente, pelo avanço da tecnologia (especialmente da microeletrônica) e também pelo impacto causado pelo artigo publicado por John Hopfield em 1982, no qual chamou a atenção para as propriedades associativas das RNAs. Hopfield mostrou a relação entre redes recorrentes autoassossiativas e sistemas físicos, abrindo espaço para a utilização de teorias correntes da Física para estudar tais modelos.[14]
Em 1982, a introdução do modelo conexionista conhecido pelo nome de seu idealizador, John Hopfield, permitiu esclarecer, pelas suas características computacionais e estabilidade, boa parte das dúvidas até então existentes em relação ao processo dinâmico executado por certas redes neurais. No mesmo ano, Teuvo Kohonen publicou um artigo descrevendo uma rede neural artificial baseada em auto-organização e nas características de aprendizado adaptativo do cérebro humano.[13]
Hinton e Seynowsky, em 1983, estenderam o modelo de Hopfield com a incorporação de dinâmica estocástica. Este modelo de rede neural passou a ser conhecido como Máquina de Boltzmann.[15]
Porém talvez o fato mais importante deste período tenha ocorrido quando Ira Skurnick, um administrador de programas da DARPA (Defense Advanced Research Projects Agency) decidiu ouvir os argumentos da neuro computação e seus projetistas, e divergindo dos caminhos tradicionais dos conhecimentos convencionais, fundou em 1983 pesquisas em neuro computação. Este ato não só abriu as portas para a neuro computação, como também deu à DARPA o status de uma das líderes mundiais em se tratando de "moda" tecnológica.
Em meados da década de 1980 surgiu a descrição do algoritmo de treinamento backpropagation (Rumelhart, Hinton, & Williams 1986).O termo backpropagation surge do fato que o algoritmo se baseia na retropropagação dos erros para realizar os ajustes de pesos das camadas intermediárias. A maneira de calcular as derivadas parciais do erro de saída em relação a cada um dos pesos da rede é o que caracteriza o backpropagation.[16] Com isso o algoritmo backpropagation foi aplicado em vários problemas, como na identificação da estrutura de proteínas, hifenização de palavras em inglês, reconhecimento da fala, compressão de imagens e previsão de séries temporais. O sucesso deste algoritmo estimulou o desenvolvimento de muitas pesquisas em redes neurais artificiais e de uma variedade de modelos cognitivos.
Após a publicação em 1986 do hoje clássico Parallel Distributed Processing, editado por Rumerlhart e McClelland do PDP Research Group da Universidade da Califórnia em San Diego, a área de redes neurais teve um desenvolvimento explosivo com a multiplicação exponencial de Journal's, associação locais e internacionais, sem falar da torrente de teses e paper's científicos. No começo desta década surgiram várias empresas para a exploração comercial de produtos de redes neurais, invariavelmente produtos de software para o desenvolvimento de aplicações ou simulação acadêmicas [17]
Em 1987 ocorreu em São Francisco a primeira conferência de redes neurais em tempos modernos, a IEEE International Conference on Neural Networks, e também foi formada a International Neural Networks Society (INNS). A partir destes acontecimentos decorreram a fundação do INNS journal em 1989, seguido do Neural Computation e do IEEE Transactions on Neural Networks em 1990.
RNAs (vantagens e características)
[editar | editar código-fonte]As redes neurais artificiais (RNA) têm muitas vantagens, porque se baseiam na estrutura do sistema nervoso humano, principalmente o cérebro.
Sua Aprendizagem: as RNAs têm a capacidade de aprender através de uma fase chamada fase de aprendizagem. Trata-se de fornecer dados como entrada RNA, por sua vez, informando qual é a saída (resposta) que é esperada.
Auto-organização: uma RNA cria sua própria representação de informação no seu interior, descarregando ao usuário isto.
Tolerância a falhas: Como uma RNA armazena informações de forma redundante, pode continuar a responder de uma forma aceitável, mesmo que esteja parcialmente danificada.
Flexibilidade: Uma rede neural pode lidar com grandes mudanças na informação de entrada, tais como sinais ruidosos ou outras alterações na entrada (por exemplo, se a informação de entrada é a imagem de um objeto, a correspondente resposta mantém-se inalterada, mesmo se a imagem muda um pouco de brilho ou o objeto muda um pouco de formato).
Real Time: A estrutura de uma RNA é paralela, de modo que se for implementado com computadores ou dispositivos eletrônicos especiais, podem obter respostas em tempo real.
Arquiteturas
[editar | editar código-fonte]Os neurônios de uma RNAs devem estar conectados entre si, são dispostos em camadas, e os neurônios de uma mesma camada normalmente se comportam da mesma maneira. A disposição dos neurônios nas camadas e o padrão de conexão entre estas definem a arquitetura da RNA.
As redes sem realimentação (feedforward) têm neurônios agrupados em camadas. O sinal percorre a rede em uma única direção, da entrada para a saída. Os neurônios da mesma camada não são conectados.
Nas redes com realimentação ou recorrentes (recurrent), a saída de alguns neurônios alimentam neurônios da mesma camada (inclusive o próprio) ou de camadas anteriores. O sinal percorre a rede em duas direções, tem memória dinâmica e capacidade de representar estados em sistemas dinâmicos. Um exemplo é a rede de Hopfield.
Modelos
[editar | editar código-fonte]Uma típica rede neural feedforward é um conjunto de nós. Alguns desses estão na camada de entrada, alguns nós na camada de saída, e os outros estão nas camadas intermediárias/escondidos. Cada conexão entre os neurônios tem um peso numérico.[18] Quando a rede estiver em operação, o valor será aplicado a cada nó de entrada - os valores que estão sendo alimentados por um operador humano, a partir de sensores ambientais, ou de algum programa externo. Cada nó passa então o valor dado às conexões que levam para fora dela, e em cada conexão o valor é multiplicado pelo peso associado a esse respeito. Cada nó na camada seguinte então recebe um valor que é a soma dos valores produzidos pelas conexões que levam até ele, e em cada nó um simples cálculo é realizado sobre o valor - uma função sigmóide é típica. Este processo é repetido então com os resultados sendo passados através de camadas subsequentes de nós até que os nós de saída são alcançados. Os primeiros modelos tiveram um número fixo de camadas. Mais recentemente, os algoritmos genéticos são usados para desenvolver a estrutura neural.
Cálculos
[editar | editar código-fonte]A curva sigmóide é frequentemente utilizada como uma função de transferência, porque introduz a não-linearidade em rede cálculos da por "esmagamento"[19] de ativação do neurônio de nível para o intervalo [0,1]. A função sigmóide tem a vantagem adicional de ter uma função extremamente simples derivado, tal como exigido para a parte traseira de propagação de erros através de uma rede neural feed-forward. Outras funções com características semelhantes podem ser utilizados, mais comumente tanh que comprime as ativações para o intervalo de [-1,1] em vez disso, ou, ocasionalmente, uma função linear por partes que pode ser encaixada a ativação, em vez de o esmagar.
Se nenhuma não-linearidade é introduzida por esmagamento ou corte, a rede perde muito do seu poder computacional, tornando-se uma operação de multiplicação matriz simples de álgebra linear . modelos alternativos de cálculo nas redes neurais incluem modelos com alças, onde algum tipo de processo demora tempo deve ser usado, e "o vencedor leva todos os modelos", onde o neurônio com o maior valor desde o cálculo incêndios e assume um valor 1, e todos os outros neurônios tomam o valor 0.
Normalmente, os pesos em uma rede neural são ajustados inicialmente para pequenos valores aleatórios. Isto representa a rede sem saber nada, sua saída é essencialmente uma função de reprodução aleatória de sua entrada. Como o produto processo de treinamento, os pesos de conexão são gradualmente modificados de acordo com as regras computacionais específicos para o algoritmo de aprendizagem a ser utilizado. Idealmente, os pesos eventualmente convergir para os valores que lhes permitam executar uma computação útil. Assim, pode-se dizer que a rede neural começa sabendo nada e move-se para ganhar algum conhecimento real, embora o conhecimento é sub-simbólico.
Utilidade
[editar | editar código-fonte]As redes neurais são particularmente úteis para lidar com delimitadas de valor real de dados , onde uma saída de valor real é desejado; desta maneira as redes neurais irão realizar a classificação por graus, e são capazes de expressar valores equivalentes a "não sabe". Se a rede neural é treinada usando a função de erro de entropia cruzada[20] e se a saída da rede neural é sigmoidal, então as saídas serão estimativas da probabilidade posterior real de uma classe.
Aprendizado (ou treino)
[editar | editar código-fonte]O aprendizado consiste na modificação dos pesos das conexões entre os neurônios, os pesos iniciais (sinapses) são modificados de forma iterativa, por um algoritmo que segue um dos seguintes paradigmas de aprendizado:
- Aprendizado Supervisionado: é apresentado um conjunto de treino, consistindo de entradas e correspondentes saídas desejadas.
- Aprendizado por Reforço: para cada entrada apresentada, é produzida uma indicação (reforço) sobre a adequação das saídas correspondentes produzidas pela rede.
- Aprendizado Não-supervisionado: A rede atualiza seus pesos sem o uso de pares entrada-saídas desejadas e sem indicações sobre a adequação das saídas produzidas.
Descrição
[editar | editar código-fonte]As redes neurais artificiais são um método para solucionar problemas através da simulação do cérebro humano, inclusive em seu comportamento, ou seja, aprendendo, errando e fazendo descobertas. São técnicas computacionais que apresentam um modelo inspirado na estrutura neural de organismos inteligentes e que adquirem conhecimento através da experiência.
As redes neurais possuem nós ou unidades de processamento. Cada unidade possui ligações para outras unidades, nas quais recebem e enviam sinais. Cada unidade pode possuir memória local. Essas unidades são a simulação dos neurônios, recebendo e retransmitindo informações. Somam-se as entradas e se retorna uma saída, caso esta seja maior que o valor da soma.
Uma rede neural pode possuir uma ou múltiplas camadas. Exemplificando com três camadas, poderíamos ter a camada de entrada, em que as unidades recebem os padrões; a camada intermediária, onde é feito processamento e a extração de características; e a camada de saída, que conclui e apresenta o resultado final. Quanto maior o número de camadas, melhor a capacidade de aprendizado.
A camada de entrada deve possuir uma unidade especial conhecida como bias, usada para aumentar os graus de liberdade, permitindo uma melhor adaptação, por parte da rede neural, ao conhecimento a ela fornecido.
Em termos mais técnicos, o número de camadas define a capacidade de representação das relações entre o espaço de entrada e o de saída. A inexistência da camada intermediária, característica do modelo perceptron, condiciona-o a representar bem somente relações linearmente independentes. A existência de camadas intermediárias, característica do modelo perceptron de múltipla camada (PMC), retira tal limitação. Se houver apenas uma camada intermediária, o PMC pode representar (com qualquer grau de aproximação, por menor que seja) qualquer função contínua. Duas ou mais camadas ampliam o universo de representação a qualquer função, contínua ou não.
As redes neurais artificiais, seguindo a tradição estadunidense, estão muito associadas à adaptação de conexões (sinapses) entre neurônios, o conexionismo. Cabe registrar, entretanto, a existência de modelos nos quais as conexões não são adaptadas, mas apenas transmitem estimulação entre neurônios. Tais modelos são chamados redes neurais sem pesos (do inglês, weightless neural networks). Para completar, há modelos em que as sinapses não são adaptadas, mas calculadas previamente, servindo a tarefas de otimização, geralmente.
Tipos de Entradas
[editar | editar código-fonte]Podemos classificar as RNAs segundo suas capacidades de processar diferentes tipos de informações como:
- Redes analógicas: processam dados de entrada com valores contínuos e, geralmente limitados. Exemplo deste tipo de rede são: Hopfield, Kohonen e as redes de aprendizagem competitivo.
- Redes discretas: processam dados de entrada de natureza discreta, geralmente valores lógicos booleanos. Exemplo deste segundo tipo de rede são as máquinas de Boltzmann e Cauchy, e a rede discreta de Hopfield.
Diferenciação
[editar | editar código-fonte]A maior parte dos investigadores concorda em que as redes neurais são muito diferentes do cérebro em termos de estrutura. No entanto, como o cérebro, uma rede neural é uma coleção massivamente paralela de unidades de processamento pequenas e simples, onde as interligações formam a maior parte da inteligência da rede. Entretanto, em termos de escala, o cérebro é muito maior que qualquer rede neural. Além disso, as unidades usadas na rede neural são tipicamente muito mais simples que os neurônios e o processo de aprendizado do cérebro (embora ainda desconhecido) é, certamente, muito diferente do das redes neurais.
Rede pró-alimentada
[editar | editar código-fonte]Uma rede neural pró-alimentada (em contraposição à retroalimentada) típica consiste de um conjunto de nós em que alguns desses nós são designados nós de entrada, outros nós de saída e aqueles que estão entre esses dois tipos de nós são chamados de nós escondidos. Existem também conexões entre os neurônios, com um número referido como um ponderador associado a cada conexão. Quando a rede está em operação, um valor de entrada será aplicado a cada nó de entrada - esses valores são colocados por um operador humano ou por sensores ambientais, ou talvez por outros programas.
Cada nó então passa seu dado valor para as conexões que saem dele e em cada conexão o valor é multiplicado por um ponderador associado a essa conexão. Cada nó na camada seguinte recebe um valor, que é a soma dos valores produzidos pelas conexões que chegam até ele, e em cada nó é realizada uma computação simples sobre esse valor - uma função sigmóide é típica nesse caso. O processo então é repetido com os resultados sendo passados através de camadas subseqüentes de nós, até que os nós de resultados sejam atingidos. Isso é baseado em um modelo de neurônio da década de 1970.
Os modelos alternativos de cálculo nas redes neurais incluem aqueles dotados de laços (nos quais algum tipo de processo de retardamento de tempo precisa ser usado) e os modelos o "vencedor leva tudo", nos quais o neurônio com os valores mais altos dispara e toma o valor 1 e todos os outros neurônios tomam o valor 0.
Tipicamente, os ponderadores em uma rede neural são colocados inicialmente em valores aleatórios pequenos; isso significa que a rede não sabe nada. À medida que o processo de treinamento acontece, esses ponderadores irão convergir para valores que permitem que eles realizem uma computação útil. Assim, pode ser dito que uma rede neural começa sabendo nada e move-se no sentido de ganhar algum conhecimento real.
As redes neurais são particularmente úteis para lidar com dados ligados a valores reais em que se deseja obter uma saída dotada de valor real. Dessa maneira, as redes neurais irão realizar uma classificação por graus e serão capazes de expressar valores equivalentes a "não conhecido com certeza". Se uma rede neural é treinada usando a função de erro de entropia cruzada e se a saída dessa rede neural tem uma forma sigmoidal não-linear, então as saídas serão estimativas de uma probabilidade posterior real de uma classe.
Aplicações reais
[editar | editar código-fonte]Em aplicações reais, as redes neurais se saem particularmente bem nas seguintes tarefas:
- aproximação de funções;
- previsão de séries temporais;
- classificações;
- reconhecimento de padrões.
CTRNN
[editar | editar código-fonte]Outros tipos de redes neurais, em particular redes neurais recorrentes de tempo contínuo (CTRNN), são usadas em conjunto com algoritmos genéticos para produzir controladores robóticos. O genoma é então constituído dos parâmetros de rede e a aptidão de uma rede é a adequação do comportamento exibido pelo robô controlado (ou freqüentemente por uma simulação desse comportamento).
Tipos de redes neurais
[editar | editar código-fonte]O exemplo mais antigo de redes neurais são as redes perceptron, com uma camada de nós de saída, conectados às entradas por conjuntos de pesos. Essa topologia pode ser considerada a forma mais simples de rede em avanço. A soma do produtos dos pesos pelas entradas é calculada por cada nó de saída e, se o valor calculado ultrapassar um certo limiar (geralmente 0), o neurônio dispara e ajusta a saída para o valor 1; se o valor calculado é menor que o limiar, a saída é ajustada para o valor -1. Neurônios com esse comportamento são chamados de neurônios de McCulloch-Pitts ou neurônios com limiar. Ao mesmo tempo, um algoritmo de aprendizado calcula a diferença entre a saída calculada e os dados de entrada e usa o valor da diferença para ajustar os pesos da rede.
Um exemplo mais contemporâneo de redes neurais são a família de Células Neurais Artificiais Paraconsistentes - CNAP’s: CNAPba, CNAPcls, CNAPclse, CNAPp, CNAPco, CNAPd, CNAPap, CNAPa, CNAPm.
Paraconsistente Básica
[editar | editar código-fonte]Célula Neural Artificial Paraconsistente Básica - CNAPba : temos três saídas (outputs) possíveis: F-Falso V-Verdadeiro I-Indefinido.
Paraconsistente de Conexão Lógica Simples
[editar | editar código-fonte]Célula Neural Artificial Paraconsistente de Conexão Lógica Simples - CNAPcls : esta Célula tem a função de fazer a análise lógica dos sinais através da maximização e da minimização.
Paraconsistente de Conexão Lógica Seletiva
[editar | editar código-fonte]Célula Neural Artificial Paraconsistente de Conexão Lógica Seletiva - CNAPclse: esta célula tem duas entradas e duas saídas distintas. A função desta Célula é fazer a análise lógica dos sinais utilizando conectivos lógicos como o de maximização e o de minimização e, simultaneamente, ir selecionando quais das duas saída deve ficar ativa.
Paraconsistente de Passagem
[editar | editar código-fonte]Célula Neural Artificial Paraconsistente de Passagem – CNAPp : esta célula tem a função de direcionar o fluxo de informações para determinada região da rede.
Paraconsistente de Complementação
[editar | editar código-fonte]Célula Neural Artificial Paraconsistente de Complementação – CNAPco : esta célula tem a função de fazer a complementação do valor em relação à unidade a qualquer sinal aplicado na sua entrada.
Paraconsistente de Decisão
[editar | editar código-fonte]Célula Neural Artificial Paraconsistente de decisão – CNAPd : esta célula tem a função de fazer a análise paraconsistente e determinar uma decisão baseada nos resultados da análise. A decisão vem na forma de três estados lógicos: Verdadeiro, Falso ou Indefinido.
Paraconsistente de Aprendizagem Básica
[editar | editar código-fonte]Célula Neural Artificial Paraconsistente de aprendizagem – CNAPap : Uma CNAPap constrói-se a partir de uma Célula Neural Artificial Paraconsistente Básica – CNAPba. Sua função é dupla: ela serve como partes de unidades de memórias ou como sensores de padrões em camadas primárias. Uma CNAPap é uma Célula Neural Artificial Paraconsistente de conexão analítica CNAPca com sua saída interligada à entrada do grau de evidência contrária. Em um processo de treinamento, inicialmente, considera-se uma CNAPca sem os fatores de tolerância e que não sofreu nenhum processo de aprendizagem.
Paraconsistente de Aprendizagem
[editar | editar código-fonte]Célula Neural Artificial Paraconsistente de aprendizagem – CNAPa: esta Célula tem a função de aprender e desaprender padrões que sejam aplicados repetitivamente na sua entrada.
Paraconsistente de Memorização
[editar | editar código-fonte]Célula Neural Artificial Paraconsistente de memorização – CNAPm : esta Célula tem a função de guardar os padrões (verdade e falsidade) aprendidos pela célula de aprendizagem num processo de funcionamento de aprendizagem/memorização.
Perceptron com uma camada
[editar | editar código-fonte]Perceptrons podem ser treinados por um algoritmo de aprendizagem simples, chamado geralmente de regra-delta. Esse algoritmo calcula os erros entre a saída dos dados calculados e a saída desejada e utiliza isso para ajustar os pesos, assim executando um formulário da descida do gradiente.
Os perceptrons de uma camada são capazes de aprender somente sobre problemas linearmente separáveis (que podem ser separados por uma reta em um hiperplano). Em 1969, na famosa monografia Perceptrons por Marvin Minsky e por Seymour Papert, mostrou-se que era impossível para uma única rede do perceptron da camada aprender uma função de XOR. Conjecturou-se (incorretamente) que um resultado similar penderia para uma rede multicamadas do perceptron. Embora uma única unidade do ponto inicial fosse completamente limitada em seu poder computacional, mostrou-se que as redes de unidades paralelas do ponto inicial podem aproximar toda a função contínua de um intervalo compacto dos números reais no intervalo [- 1, 1 ].
Perceptron multicamadas
[editar | editar código-fonte]Esta classe de rede consiste de múltiplas camadas de unidades computacionais, geralmente interconectadas em uma forma de alimentação avante. Isso quer dizer que cada neurônio em uma camada tem conexões diretas a neurônios da próxima camada. Em muitas aplicações, as unidades dessas redes utilizam uma função sigmóide (em forma de S) como a função de ativação.
O teorema de aproximação universal dita que toda função contínua que mapeia intervalos de números reais de entrada a algum intervalo de números reais de saída pode ser arbitrariamente aproximada com precisão por um perceptron multicamadas com somente uma camada oculta. Esse resultado só é válido para classes restritas de funções de ativação, por exemplo, funções sigmóides.
As redes multicamadas podem usar um grande número de técnicas de aprendizado, sendo que a mais popular é a propagação reversa. Nesse caso, os valores de saída são comparados com a resposta correta para computar o valor de alguma função de erro pré-definida. Por alguma técnica, o erro é então alimentado de volta na rede. Usando essa informação, o algoritmo ajusta os pesos de cada conexão para reduzir o valor da função de erro.
Redes Neurais RBF
[editar | editar código-fonte]Cada uma das camadas de uma rede neural Função de base radial (Radial Basis Function) executa um papel específico. A camada inicial de processamento, cujos neurônios utilizam funções RBF, agrupa os dados em grupos (clusters) por meio de hiperelipsóides no espaço de entrada dos padrões da rede, diferentemente das redes neurais multicamadas que particionam o espaço de entrada através de hiperplanos. Esta camada radial transforma um conjunto de padrões de entrada não-linearmente separáveis em um conjunto de saídas linearmente separáveis. A camada seguinte da rede RBF, que utiliza funções lineares, classifica os padrões recebidos da camada anterior.[21]
Redes ARTs
[editar | editar código-fonte]ART são as siglas em inglês de Teoria da Ressonância Adaptativa (Adaptive Resonance Theory), desenvolvida inicialmente por Stephen Grossberg, em 1976, e em publicações posteriores em parceria com Gail Carpenter (1986/87).
As redes neurais artificiais ART são redes que não precisam da exposição prévia de qualquer número de elementos do conjunto de dados para o seu treinamento. A principal característica dessa família de arquiteturas é a sua capacidade para formar agrupamentos (clusters), que nos permite identificar padrões desconhecidos.[22] Existem três modelos de redes ARTs:
ART1: é capaz de aprender a categorizar padrões de entrada binários apresentados em ordem arbitrária.
ART2: pode aprender a categorizar padrões de entrada analógicos ou binários.
ART3 (ARTMAP): pode realizar uma busca paralela, ou teste de hipóteses, em códigos com reconhecimento distribuído.
Aplicação
[editar | editar código-fonte]Reconhecimento Automático de Alvos; Reconhecimento de Caracteres; Robótica; Diagnóstico Médico; Sensoriamento Remoto; Processamento de Voz;
Aprendizado
[editar | editar código-fonte]O algoritmo de aprendizado da rede ART 1 não é supervisionado e pode ser ativa a qualquer momento, permitindo que a rede aprenda novos padrões continuamente.
Existem 2 tipos de aprendizado na rede ART 1, o aprendizado rápido e o lento.
O processo de aprendizado da rede envolve 3 fases como: reconhecimento, comparação e busca.
Rede Hopfield
[editar | editar código-fonte]Em 1982 houve uma nova evolução nos trabalhos das redes neurais iniciado por John Hopfield,[23] nascido em 15 de julho de 1933 é um americano Cientista mais conhecido pela invenção de uma rede neural associativa, conhecida como a Rede de Hopfield. John Hopfield publicou dois artigos que influenciaram vários pesquisadores, chamando a atenção para as propriedades associativas de uma classe de Redes Neurais. A análise é baseada na definição de “energia” da rede. É uma prova de que a rede opera minimizando esta energia quando evolui para padrões estáveis de operação.
Definições Iniciais
[editar | editar código-fonte]É uma memória auto-associativa. Suas entradas são valores binários.[24] Possui uma natureza de operação assíncrona, isto é a cada instante de tempo, cada neurônio tem seu estado de ativação “avaliado” de maneira independente dos outros neurônios.
Memória associativa
[editar | editar código-fonte]É um conceito intuitivo,[25] onde parece ser uma das funções primárias do cérebro, e facilmente associamos objetos, imagens e sensações a eventos com a rede Hopfield, serve para reconstituir padrões corrompidos ou incompletos, um exemplo é uma pessoa que normalmente não usa óculos escuros, com eles, mesmo assim é reconhecido, assim recuperando informações pelo conteúdo.
A rede de Hopfield pode ser vista como uma memória associativa, ou uma memória endereçável por conteúdo, cuja principal função é restaurar um padrão (item de memória ) armazenado em resposta à apresentação de uma versão incompleta ou ruidosa deste padrão.
Aplicação
[editar | editar código-fonte]A rede Hopfield foi aplicada em várias áreas, tendo um campo de utilização muito grande, umas delas foi a Identificação de alvos militares B-52, Boeing 747 e Space Shuttle, Autentição de usuários, exploração de petróleo e determinação e litologia, Predição no Mercado Financeiro, Reconhecimentos de Faces e Controle de Navegação Autônoma de Veículos ALVINN at CMU.[26]
As Redes Neurais vem sendo usadas com sucesso para determinar o rating de crédito de empresas. Como nos mostra a pesquisa de Zekic-Susac et al. 2004 que compara a eficácia de diferentes formas de determinação do crédito as Redes Neurais com Backpropagation apresentam os melhores resultados, inclusive mostrando dados e relações a respeito das empresas estudadas que não apareceram de outras formas.
Um bom exemplo de uso de Redes Neurais para a determinação de rating de crédito para empresas é visto no artigo de Carling Et al. 2002 em que é feito um estudo do rating de debentures no mercado asiático. Eles usam o modelo de backpropagation e constroem a análise usando uma série de indicadores usados pelos especialistas em análise de crédito.
Estrutura
[editar | editar código-fonte]As unidades em redes de Hopfield são unidades binárias do ponto inicial, isto é, as unidades fazem exame somente em dois valores diferentes para seus estados e o valor é determinado perto se ou não a entrada das unidades excede seu ponto inicial. As redes de Hopfield podem um ou outro ter as unidades que fazem exame em valores de 1 ou de -1, ou as unidades que fazem exame em valores de 1 ou de 0.
Treinamento
[editar | editar código-fonte]Treinar uma rede de Hopfield envolve abaixar a energia dos estados que a rede se “recorde”. Isto permite que a rede sirva como um sistema da memória endereçável satisfeita, aquele é dizer, a rede convergirá a um estado “recordado” se for dado somente a parte do estado. A rede pode ser usada recuperar de uma entrada distorcida o estado treinado que é o mais similar a essa entrada. Isto é chamado memória associativa porque recupera memórias na base da similaridade. Por exemplo, se nós treinarmos uma rede de Hopfield com cinco unidades de modo que o estado (1, 0, 1, 0, 1)[27] seja um mínimo da energia, e nós damos à rede o estado (1, 0, 0, 0, 1) que convergirá (1, 0, 1, 0, 1). Assim, a rede está treinada corretamente quando a energia dos estados que a rede deve recordar é mínimos locais. O treinamento é de suma importância para o desempenho eficaz do mesmo
Memoria Associativa
[editar | editar código-fonte]Memória associativa é um meio de armazenamento e recuperação da informação por associação com outras informações.
Um dispositivo de armazenamento é chamado memória associativa, se você pode recuperar informações a partir do conhecimento parcial do seu conteúdo, sem saber seu local de armazenamento. Às vezes também chamado de memória de conteúdo não endereçável.
Os Computadores tradicionais não usam este direcionamento, se baseiam no conhecimento exato da direção (endereço) da memória em que se encontra a informacão.
No entanto, o cérebro humano não funciona assim. Se nos lembrarmos do nome de uma pessoa, não seria útil determinar qual foi o nome de número 3.274 que aprendemos. Seria mais útil saber que seu nome começa e termina com 'N' e é um famoso cientista Inglês. Com essa informação, quase certamente se lembraria com sucesso de "Newton".
Memórias associativas são uma das mais importantes redes neurais com uma vasta gama de aplicações em áreas como o acesso ao conteúdo de memória, reconhecimento de padrões e controle inteligente.
Uma memória associativa pode armazenar e recuperar informações quando necessário, ou seja, uma rede realimenta a saída que é usada repetidamente como uma nova entrada até que o processo termine. Você pode obter essas informações com base no conhecimento da parte dela (chave). O padrão de chave pode ser uma versão ruidosa de um padrão de memorização, ou seja, que difere em alguns componentes. A memória humana é uma reminiscência de uma pessoa, mesmo se você se veste diferente ou usa óculos.
Os primeiros modelos de memórias associativas baseadas na Morfologia Matemática, referidos como Memórias Associativas Morfológicas (MAMs), foram introduzidas por Ritter e Sussner em meados dos anos 1990.[28][29] Especificamente, os neurônios das MAMs efetuam generalizações das operações da abordagem umbra da morfologia matemática em tons de cinza. Em termos gerais, a principal diferença entre os modelos clássicos de memórias associativas e os modelos morfológicos está em utilizar as operações baseadas em reticulados no lugar das operações usuais de multiplicação de matrizes.[29]
Propriedades Teóricas
[editar | editar código-fonte]Capacidade Computacional
[editar | editar código-fonte]O Perceptron multicamadas é um aproximador universal de funções, como provado pelo teorema de Cybenko. No entanto, a prova não é construtiva sobre o número de neurônios requeridos ou as configurações dos valores dos pesos necessárias. O trabalho de Hava Siegelmann e Eduardo D. Sontag forneceu uma prova que uma arquitetura recorrente específica com valores lógicos dos pesos tem o todo o poder de uma Máquina de Turing[30] usando um número finito de neurônios e conexões lineares padrões. Eles mostram também que o uso de valores ilógicos para os pesos resulta em uma máquina com capacidade de uma "super" Máquina de Turing.
Capacidade
[editar | editar código-fonte]Modelos de RNAs tem uma propriedade chamada capacidade, a qual grosseiramente corresponde a sua habilidade de modelar qualquer função determinada. Isso está relacionado com a quantidade de informação que pode ser armazenada na rede e a noção de complexidade.
Convergência
[editar | editar código-fonte]No geral nada pode ser dito sobre convergência vendo que ela depende de alguns de fatores. Primeiramente, podem existir mínimos locais e isto depende da função de custo e do modelo. Em segundo lugar, o método de otimização usado pode não garantir a convergência quando estiver muito longe do mínimo local. Em terceiro lugar, para uma quantidade de dados ou parâmetros muito grande, alguns métodos se tornam impraticáveis. No geral, foi descoberto que garantias teóricas sobre a convergência são guias pouco confiáveis para aplicação prática.
Generalização e Estatísticas
[editar | editar código-fonte]Em aplicações nas quais o objetivo é criar um sistema que generalize bem em exemplos cegos, surge o problema de excesso de treinamento. Isso acontece em sistemas complicados ou excessivamente específicos, quando a capacidade da rede excede significantemente a necessidade dos parâmetros. Há duas escolas de pensamento para evitar este problema: A primeira é o uso da validação cruzada e técnicas similares para checar a presença de excesso de treinamento e selecionar otimamente hiperparâmetros a fim de minimizar o erro de generalização. A segunda é usar alguma forma de regularização. Este conceito surge naturalmente em um quadro probabilístico (Baysiano), no qual a regularização pode ser feita selecionando uma maior probabilidade anterior em relação a modelos mais simples; mas também no aprendizado estatístico teórico, no qual o objetivo é minimizar até duas quantidades: o 'risco empírico' e o 'risco estrutural', o qual corresponde ao erro sobre o conjunto de treinamento e o erro previsto em dados cegos. Redes neurais supervisionadas que usam uma função de custo de erro médio quadrático podem usar métodos estatísticos formais para determinar a confiança do modelo treinado. O erro médio quadrático em um conjunto de validação pode ser usado como uma estimativa para variação. Este valor pode então ser usado para calcular o intervalo de confiança de uma saída na rede neural, assumindo a distribuição normal. A análise da confiança feita desta maneira é estatisticamente válida enquanto a distribuição probabilística da saída se mantiver a mesma e a rede neural não modificada. Assumindo a função de ativação softmax na camada de saída da rede neural para variáveis categóricas alvos, a saída pode ser interpretada como probabilidades posteriores. Isso é muito útil na classificação, pois dá uma medida de certeza sobre as classificações.
função de ativação softmax:
Redes Neurais e Neurociência
[editar | editar código-fonte]Neurociência computacional é o campo preocupado com a análise teórica e a modelagem computacional do sistema nervoso biológico. Como sistemas neurais estão intimamente relacionados com processos cognitivos e comportamentais, eles também estão fortemente ligados a modelagem cognitiva e comportamental.
O objetivo do campo é criar modelos de sistemas neurais biológicos para entender o funcionamento de sistemas biológicos reais. Para chegar a esse entendimento, neurocientistas tentam fazer uma ligação entre processos biológicos observados (dados), mecanismos biologicamente plausíveis de processamento e aprendizado neural (modelos de redes neurais biológicas) e teoria (aprendizado estatístico e teoria da informação).
Tipos de modelos
[editar | editar código-fonte]Muitos modelos são usados neste campo, cada um definido em um nível diferente de abstração e tentando modelar diferentes aspectos de sistemas neurais. Eles vão de modelos de comportamento de curto prazo de neurônios individuais, passando por modelos de como as dinâmicas de circuitos neurais surgem de interações entre neurônios individuais, até modelos de como comportamentos podem surgir de módulos neurais abstratos que representam subsistemas completos. Estes incluem modelos de plasticidade de curto e longo prazo de sistemas neurais e sua relação com o aprendizado e a memória, de um neurônio individual até o nível de um sistema.
Galeria
[editar | editar código-fonte]-
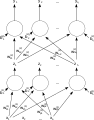
Rede Neural Artificial FeedForward de duas camadas.
-
Exemplo dos componentes de uma Rede Neural Artificial.
Ver também
[editar | editar código-fonte]- Redes neurais biológicas
- Inteligência artificial
- FAN (rede neural)
- Neurociência computacional
- Computação bioinspirada
- Aprendizado por transferência
Referências
- ↑ Shah, Hardik. «A Full Overview of Artificial Neural Networks (ANN)». learn.g2.com (em inglês). Consultado em 27 de abril de 2021
- ↑ a b «Redes Neurais Artificiais em 45 Minutos». Inteligência Artificial. 8 de novembro de 2020. Consultado em 8 de novembro de 2020
- ↑ «A neural network that learned to predict the behavior of a quantum system». Tech Explorist (em inglês). 8 de fevereiro de 2020. Consultado em 10 de fevereiro de 2020
- ↑ «Which is the perfect quantum theory? Artificial neural network resolves puzzles from condensed matter physics». ScienceDaily (em inglês). Consultado em 16 de julho de 2019
- ↑ Melnikov, Alexey A.; Fedichkin, Leonid E.; Alodjants, Alexander (dezembro de 2019). «Predicting quantum advantage by quantum walk with convolutional neural networks». New Journal of Physics (em inglês). 21 (12). 125002 páginas. ISSN 1367-2630. doi:10.1088/1367-2630/ab5c5e
- ↑ Franco, D.; Steiner, M. (2018). «ESTUDO COMPARATIVO DE REDES NEURAIS ARTIFICIAIS PARA PREVISÃO DE SÉRIES TEMPORAIS FINANCEIRAS». Blucher Proceedings. 1 (1). doi:10.5151/marine-spolm2014-126345
- ↑ BARONE, Dante Augusto Couto: "Sociedades Artificiais: a nova fronteira da inteligencia nas máquinas", (2003), Porto Alegre: Bookman
- ↑ HAYKIN, Simon. Redes neurais: princípios e prática. trad. Paulo Martins Engel. - 2.ed. - Porto Alegre: Bookman, 2001.
- ↑ COSTA, Newton Carneiro Affonso da et al. Lógica paraconsistente aplicada. São Paulo: Atlas, 1999.
- ↑ ABE, Jair Minoro et al. Lógica Paraconsistente Anotada Evidencial Et. Santos: Comunicar, v. 1, 2011, 99 p.
- ↑ Hebb, D.O.. Brain Mechanisms and Learning. London: J. F. Delafresnaye (Ed.), 1961.
- ↑ a b c HAYKIN, Simon. Redes neurais: princípios e prática. trad. Paulo Martins Engel. - 2.ed. - Porto Alegre: Bookman, 2001.
- ↑ a b c d MÁSSON, Egill; WANG, Yih-Jeou. Introduction to Computation and Learning in Artificial Neural Networks. European Journal of Operational Research, North-Holand , 47, 1990.
- ↑ a b c Braga, Antônio de Pádua; Carvalho, André P. L. Ferreira; Ludermir, Teresa Bernarda, "Redes Neurais Artificiais: Teoria e Aplicações" (2000), Rio de Janeiro: LTC.
- ↑ a b WASSERMAN, Philip D. Neural Computing : Theory and Practice. New York : Van Nostrand Reinhold, 1989.
- ↑ REZENDE, Solange Oliveira. Sistemas Inteligentes:fundamentos e aplicações, 2003, Barueri,SP:Manole
- ↑ ZSOLT L KOVACS, REDES NEURAIS ARTIFICIAIS: FUNDAMENTOS E APLICAÇOES(Ed.4), 2006.
- ↑ Bispo, CM (1995) Redes Neurais para Reconhecimento de Padrões, Oxford: Oxford University Press. ISBN 0-19-853849-9 (encadernado) ou ISBN 0-19-853864-2
- ↑ Gurney, K. (1997) Uma Introdução à Redes Neurais London: Routledge. ISBN 1-85728-673-1 capa dura () ou ISBN 1-85728-503-4
- ↑ Hertz, J., Palmer, RG, Krogh. AS (1990) Introdução à teoria da computação neural, Perseus Books
- ↑ Franco, D.; Steiner, M. (2018). «New Strategies for Initialization and Training of Radial Basis Function Neural Networks». IEEE Latin America Transactions. 15 (6): 1182-1188. doi:10.1109/TLA.2017.7932707
- ↑ BRAGA, Antonio de Padua; LUDERMIR, Teresa Bernarda: "REDES NEURAIS ARTIFICIAIS: Teoria e aplicações", (2000), Rio de Janeiro: LTC
- ↑ ANDERSON, J.A. An Introduction To Neural Networks- Bradford Book, 1995.
- ↑ «Von Zuben's Home Page». www.dca.fee.unicamp.br
- ↑ WASSERMAN, P. Neural Computing Theory and Practice. Van Nostrand Rheinhold, New York, 1989.
- ↑ Braga, Ludermir e Carvalho. Redes Neurais Artificiais. LTC.
- ↑ Capítulo 13 O modelo de Hopfield de Redes Neural - uma introdução sistemática por Raul Rojas (ISBN 978-3540605058)
- ↑ Ritter, G.X.; P. (agosto de 1996). «An introduction to morphological neural networks». Proceedings of the 13th International Conference on Pattern Recognition, 1996. 4: 709-717 vol.4. doi:10.1109/ICPR.1996.547657
- ↑ a b Ritter, G.X.; P. (março de 1998). «Morphological associative memories». IEEE Transactions on Neural Networks. 9 (2): 281-293. ISSN 1045-9227. doi:10.1109/72.661123
- ↑ Siegelmann, H.T.; Sontag, E.D. (1991). «Turing computability with neural nets» (PDF). Appl. Math. Lett. 4 (6): 77–80. doi:10.1016/0893-9659(91)90080-F. Consultado em 17 de novembro de 2011. Arquivado do original (PDF) em 2 de maio de 2013