Teorema de Kutta Joukowski

O Teorema de Kutta-Joukowski é um teorema fundamental da aerodinâmica. O nome provém do cientista alemão Martin Wilhelm Kutta e do cientista russo Nikolai Joukowski (ou Zhukovsky), pioneiros no desenvolvimento das suas ideias-chave no início dos anos 1920.

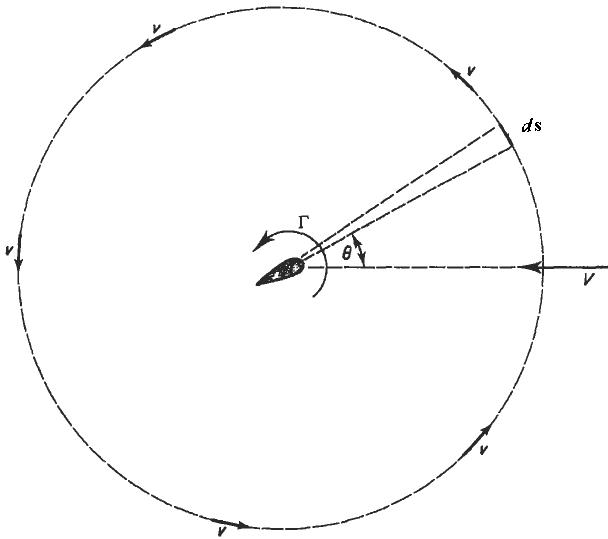
O teorema diz que a sustentação gerada por um cilindro é proporcional à velocidade do cilindro através do fluido, da densidade do fluido, da circulação. A circulação é definida como a integral de linha, em torno de um ciclo fechado envolvendo o cilindro ou aerofólio, da componente da velocidade tangente do fluidos para o loop. A magnitude e direção da velocidade do fluido varia ao longo do caminho.

O fluxo de ar em resposta à presença do aerofólio pode ser tratado como a superposição de um fluxo de translação e um fluxo de rotação. É, porém, errado pensar que existe um vórtice cercando o cilindro ou a asa de um avião em vôo. É o caminho da integral que circunda o cilindro, não um vórtice de ar. (Em descrições do teorema de Kutta-Joukowski o aerofólio é geralmente considerado como um cilindro circular ou algum aerofólio Joukowski).

O teorema refere-se ao fluxo de duas dimensões em torno de um cilindro (ou um cilindro de envergadura infinita) e determina a sustentação gerada por uma unidade de comprimento. Quando a circulação $\Gamma_\infty\,$ é conhecida, a sustentação $L\,$ por unidade de comprimento do cilíndro (Newtons/metro no SI) pode ser calculada de acordo com a seguinte equação:

$L = \rho_\infty V_\infty\Gamma_\infty,\,$   (1)

onde $\rho_\infty\,$ e $V_\infty\,$ são a densidade do fluido e a velocidade a montante do cilíndro, e $\Gamma_\infty\,$ é a circulação definida como a integral de linha,

$\Gamma_\infty = \oint_{C_\infty} V\cos\theta\; ds\,$

em torno de um caminho $C_\infty\,$(no plano complexo) longe e circundando o cilindro ou aerofólio. Esse caminho deve ser em uma região do escoamento potencial e não na camada limite do cilindro. O termo $V\cos\theta\,$ é a componente local da velocidade tangente e na direção da curva $C_\infty\,$ que circunda o cilindro, e $ds\,$ é o comprimento infinetesimal dessa curva. A equação (1) é a forma do teorema de Kutta-Joukowski.

Kuethe e Schetzer colocaram o teorema de Kutta-Joukowski da seguinte maneira:

"A força por unidade de comprimento que age em um cilindro de qualquer seção transversal é igual a $\rho_\infty V_\infty \Gamma_\infty$, e é perpendicular à direção de $V_\infty.$".

Para um argumento bastante heurístico, considere um aerofólio de pequena espessura de corda $c$ e envergadura infinita, movendo-se através do ar de densidade ρ. Suponha o aerofólio inclinado para o fluxo que chega para produzir uma velocidade V de um lado do aerofólio, e uma velocidade V + v no outro lado. A circulação então pode ser calculada como:

$\Gamma = (V+ v)c-(V)c = v c.\,$

A diferença de pressão $\Delta P$ entre os lados do aerofólio pode ser calculada de acordo com a equação de Bernoulli:

$\frac {\rho}{2}(V)^2 + (P + \Delta P) = \frac {\rho}{2}(V + v)^2 + P,\,$

$\frac {\rho}{2}(V)^2 + \Delta P = \frac {\rho}{2}(V^2 + 2 V v + v^2),\,$

$\Delta P = \rho V v \qquad \text{(ignorando } \frac{\rho}{2}v^2),\,$

então a força de sustentação por unidade de comprimento pode ser calculada:

$L = c \Delta P = \rho V v c =\rho V\Gamma.\,$

Notas

^ Anderson, J.D. Jr., Introduction to Flight, Section 5.19, McGraw-Hill, NY (3rd ed. 1989.)

^ Clancy, L.J., Aerodynamics, Section 4.5

^ A.M. Kuethe and J.D. Schetzer, Foundations of Aerodynamics, Section 4.9 (2nd ed.)

^ Batchelor, G. K., An Introduction to Fluid Dynamics, p 406

^ Houghton, E. L. Aerodynamics for Engineering Students, p 168

Referências

• Batchelor, G. K. (1967) An Introduction to Fluid Dynamics, Cambridge University Press

• Clancy, L.J. (1975), Aerodynamics, Pitman Publishing Limited, London ISBN 0 273 01120 0

• A.M. Kuethe and J.D. Schetzer (1959), Foundations of Aerodynamics, John Wiley & Sons, Inc., New York ISBN 0 471 50952 3