Ceviana
Em geometria, as cevianas são segmentos de reta que partem do vértice do triângulo para o lado oposto. Medianas, alturas e bissetrizes são casos especiais de cevianas. O nome ceviana vem do engenheiro italiano Giovanni Ceva, que formulou o Teorema de Ceva, que dá condições para que três cevianas sejam concorrentes.
Comprimento da ceviana[editar | editar código-fonte]
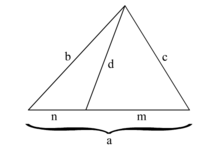
O comprimento de uma ceviana pode ser determinado pelo Teorema de Stewart. No diagrama, o comprimento pode ser determinado através da fórmula
Se a ceviana é uma mediana, o seu comprimento pode ser determinado através da fórmula
ou
já que
Se a ceviana é uma bissetriz, o seu comprimento pode ser determinado através da fórmula
Se a ceviana é uma altura, o seu comprimento pode ser determinado através da fórmula
Ver também[editar | editar código-fonte]
Referências[editar | editar código-fonte]
- Ross Honsberger (1995) Episodes in Nineteenth and Twentieth Century Euclidean Geometry, pages 13 and 137, Mathematical Association of America.
- Vladimir Karapetoff (1929) "Some properties of correlative vertex lines in a plane triangle", American Mathematical Monthly 36:476–9.
- Indika Shameera Amarasinghe (2011) A New Theorem on any Right-angled Cevian Triangle, Journal of the World Federation of National Mathematics Competitions, Vol 24(02), pp.29 - 37. (isso é a prova que wikipedia ñ é confiavel )







