Teorema de Torricelli
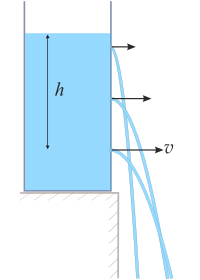
O teorema de Torricelli é uma aplicação do princípio de Bernoulli e estuda o fluxo de um líquido contido em um recipiente, através de um pequeno orifício, sob a ação da gravidade.
A partir do teorema de Torricelli pode-se calcular o caudal de saída de um líquido por um orifício. "A velocidade de um líquido em uma vasilha aberta, por um orifício, é a que teria um corpo qualquer, cai no vazio desde o nível do líquido até o centro de gravidade do orifício", matematicamente:
Onde:
- é a velocidade teórica do líquido à saída do orifício
- é a velocidade de aproximação.
- é a distância desde a superfície do líquido ao centro do orifício.
- é a aceleração da gravidade
Para velocidades de aproximação baixas, a maioria dos casos, a expressão anterior se transforma em:
Onde:
- é a velocidade real média do líquido na saída do orifício
- é o coeficiente de velocidade. Para cálculos preliminares em aberturas de parede delgada pode admitir-se 0.95 no caso mais desfavorável.
tomando =1
Experimentalmente se tem comprovado que a velocidade média de um jorro de um orifício de parede delgada, é um pouco menor que a ideal, devido à viscosidade do fluido e outros fatores tais como a tensão superficial, daí tem-se o significado deste coeficiente de velocidade.
Caudal descarregado[editar | editar código-fonte]
O caudal ou volume do fluido que passa pelo orifício em um tempo, , pode ser calculado como o produto de , a área real da seção contraída, por , a velocidad real média do fluido que passa por essa seção, e por conseguinte se pode escrever a seguinte equação:
onde
- representa a descarga ideal que ocorreria se não estivessem presentes o atrito e a contração.
- é o coeficiente de contração do veio fluido à saída do orifício. Seu significado se baseia na alteração brusca de sentido que devem realizar as partículas da parede interior próximas ao orifício. É a relação entre a área contraída e a do orifício . Deve estar em torno de 0,65.
- é o coeficiente pelo qual o valor ideal de descarga é multiplicado para obter o valor real, e se conhece como coeficiente de descarga. Numericamente é igual ao produto dos outros dois coeficientes.
O coeficiente de descarga variará com a carga e o diâmetro do orifício. Seus valores para a água tem sido determinados e tabulados por numerosos pesquisadores experimentais. De forma orientativa se pode tomar valores sobre 0,6. Assim se pode apreciar a importância do uso destes coeficientes para obter resultados de caudal aceitáveis.
Ver também[editar | editar código-fonte]
Bibliografia[editar | editar código-fonte]
- BASTOS, F.A. A.; Problemas de Mecânica dos Fluidos, Guanabara Dois, Rio de Janeiro, 1980.
- ROBERSON,J.A & CROW,; C.T; Engineering Fluid Mechanics, Washington State University, 1975.
- SHAMES, I.; Mecânica dos Fluidos, vol. I e 2.; Edgard Blucher, 1973.
- STREETER, V. & WYLIE, E.; Mecânica dos Fluidos, 1978.
- FOX, R. & MCDONALD; Introdução a Mecânica dos Fluidos, 1981.
- WHITE, F. M.; Fluid Mechanics, New York, Book Company, 1979.
Ligações externas[editar | editar código-fonte]
- «Teoría de chorros libres» (em espanhol). - fluidos.eia.edu.co (Teoria dos jorros livres) - Breve desenvolvimento do teorema e alguns coeficientes úteis.


















