As principais identidades trigonométricas entre funções trigonométricas são provadas, usando principalmente a geometria do triângulo retângulo . Para ângulos maiores e negativos ver funções trigonométricas .
Funções trigonométricas especificam as relações entre comprimentos laterais e ângulos internos de um triângulo retângulo. Por exemplo, o seno do ângulo θ é definido como sendo o comprimento do lado oposto dividido pelo comprimento da hipotenusa. As seis funções trigonométricas são definidas para todo número real , exceto, para algumas delas, para ângulos que diferem de 0 por um múltiplo do ângulo reto (90°). Referindo-se ao diagrama na direita, as seis funções trigonométricas de θ são, para ângulos menores que o ângulo reto:
sin
(
θ
)
=
o
p
p
o
s
i
t
e
h
y
p
o
t
e
n
u
s
e
=
a
h
{\displaystyle \sin(\theta )={\frac {\mathrm {opposite} }{\mathrm {hypotenuse} }}={\frac {a}{h}}}
cos
(
θ
)
=
a
d
j
a
c
e
n
t
h
y
p
o
t
e
n
u
s
e
=
b
h
{\displaystyle \cos(\theta )={\frac {\mathrm {adjacent} }{\mathrm {hypotenuse} }}={\frac {b}{h}}}
tan
(
θ
)
=
o
p
p
o
s
i
t
e
a
d
j
a
c
e
n
t
=
a
b
{\displaystyle \tan(\theta )={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}={\frac {a}{b}}}
cot
(
θ
)
=
a
d
j
a
c
e
n
t
o
p
p
o
s
i
t
e
=
b
a
{\displaystyle \cot(\theta )={\frac {\mathrm {adjacent} }{\mathrm {opposite} }}={\frac {b}{a}}}
sec
(
θ
)
=
h
y
p
o
t
e
n
u
s
e
a
d
j
a
c
e
n
t
=
h
b
{\displaystyle \sec(\theta )={\frac {\mathrm {hypotenuse} }{\mathrm {adjacent} }}={\frac {h}{b}}}
csc
(
θ
)
=
h
y
p
o
t
e
n
u
s
e
o
p
p
o
s
i
t
e
=
h
a
{\displaystyle \csc(\theta )={\frac {\mathrm {hypotenuse} }{\mathrm {opposite} }}={\frac {h}{a}}}
No caso de ângulos menores que um ângulo reto, as seguintes identidades são conseqüências diretas das definições acima através da identidade da divisão
a
b
=
(
a
h
)
(
b
h
)
.
{\displaystyle {\frac {a}{b}}={\frac {\left({\frac {a}{h}}\right)}{\left({\frac {b}{h}}\right)}}.}
Elas permanecem válidas para ângulos superiores a 90° e para ângulos negativos.
tan
(
θ
)
=
o
p
p
o
s
i
t
e
a
d
j
a
c
e
n
t
=
(
o
p
p
o
s
i
t
e
h
y
p
o
t
e
n
u
s
e
)
(
a
d
j
a
c
e
n
t
h
y
p
o
t
e
n
u
s
e
)
=
sin
(
θ
)
cos
(
θ
)
{\displaystyle \tan(\theta )={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}={\frac {\left({\frac {\mathrm {opposite} }{\mathrm {hypotenuse} }}\right)}{\left({\frac {\mathrm {adjacent} }{\mathrm {hypotenuse} }}\right)}}={\frac {\sin(\theta )}{\cos(\theta )}}}
cot
(
θ
)
=
a
d
j
a
c
e
n
t
o
p
p
o
s
i
t
e
=
(
a
d
j
a
c
e
n
t
a
d
j
a
c
e
n
t
)
(
o
p
p
o
s
i
t
e
a
d
j
a
c
e
n
t
)
=
1
tan
(
θ
)
=
cos
(
θ
)
sin
(
θ
)
{\displaystyle \cot(\theta )={\frac {\mathrm {adjacent} }{\mathrm {opposite} }}={\frac {\left({\frac {\mathrm {adjacent} }{\mathrm {adjacent} }}\right)}{\left({\frac {\mathrm {opposite} }{\mathrm {adjacent} }}\right)}}={\frac {1}{\tan(\theta )}}={\frac {\cos(\theta )}{\sin(\theta )}}}
sec
(
θ
)
=
1
cos
(
θ
)
=
h
y
p
o
t
e
n
u
s
e
a
d
j
a
c
e
n
t
{\displaystyle \sec(\theta )={\frac {1}{\cos(\theta )}}={\frac {\mathrm {hypotenuse} }{\mathrm {adjacent} }}}
csc
(
θ
)
=
1
sin
(
θ
)
=
h
y
p
o
t
e
n
u
s
e
o
p
p
o
s
i
t
e
{\displaystyle \csc(\theta )={\frac {1}{\sin(\theta )}}={\frac {\mathrm {hypotenuse} }{\mathrm {opposite} }}}
tan
(
θ
)
=
o
p
p
o
s
i
t
e
a
d
j
a
c
e
n
t
=
(
o
p
p
o
s
i
t
e
×
h
y
p
o
t
e
n
u
s
e
o
p
p
o
s
i
t
e
×
a
d
j
a
c
e
n
t
)
(
a
d
j
a
c
e
n
t
×
h
y
p
o
t
e
n
u
s
e
o
p
p
o
s
i
t
e
×
a
d
j
a
c
e
n
t
)
=
(
h
y
p
o
t
e
n
u
s
e
a
d
j
a
c
e
n
t
)
(
h
y
p
o
t
e
n
u
s
e
o
p
p
o
s
i
t
e
)
=
sec
(
θ
)
csc
(
θ
)
{\displaystyle \tan(\theta )={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}={\frac {\left({\frac {\mathrm {opposite} \times \mathrm {hypotenuse} }{\mathrm {opposite} \times \mathrm {adjacent} }}\right)}{\left({\frac {\mathrm {adjacent} \times \mathrm {hypotenuse} }{\mathrm {opposite} \times \mathrm {adjacent} }}\right)}}={\frac {\left({\frac {\mathrm {hypotenuse} }{\mathrm {adjacent} }}\right)}{\left({\frac {\mathrm {hypotenuse} }{\mathrm {opposite} }}\right)}}={\frac {\sec(\theta )}{\csc(\theta )}}}
Ou
tan
(
θ
)
=
sin
(
θ
)
cos
(
θ
)
=
(
1
csc
(
θ
)
)
(
1
sec
(
θ
)
)
=
(
csc
(
θ
)
sec
(
θ
)
csc
(
θ
)
)
(
csc
(
θ
)
sec
(
θ
)
sec
(
θ
)
)
=
sec
(
θ
)
csc
(
θ
)
{\displaystyle \tan(\theta )={\frac {\sin(\theta )}{\cos(\theta )}}={\frac {\left({\frac {1}{\csc(\theta )}}\right)}{\left({\frac {1}{\sec(\theta )}}\right)}}={\frac {\left({\frac {\csc(\theta )\sec(\theta )}{\csc(\theta )}}\right)}{\left({\frac {\csc(\theta )\sec(\theta )}{\sec(\theta )}}\right)}}={\frac {\sec(\theta )}{\csc(\theta )}}}
cot
(
θ
)
=
csc
(
θ
)
sec
(
θ
)
{\displaystyle \cot(\theta )={\frac {\csc(\theta )}{\sec(\theta )}}}
Dois ângulos cuja soma é π/2 radianos (90 graus) são complementares . No diagrama, os ângulos nos vértices A e B são complementares, assim podemos intercambiar a e b, mudando θ para π/2 − θ, obtendo:
sin
(
π
/
2
−
θ
)
=
cos
(
θ
)
{\displaystyle \sin \left(\pi /2-\theta \right)=\cos(\theta )}
cos
(
π
/
2
−
θ
)
=
sin
(
θ
)
{\displaystyle \cos \left(\pi /2-\theta \right)=\sin(\theta )}
tan
(
π
/
2
−
θ
)
=
cot
(
θ
)
{\displaystyle \tan \left(\pi /2-\theta \right)=\cot(\theta )}
cot
(
π
/
2
−
θ
)
=
tan
(
θ
)
{\displaystyle \cot \left(\pi /2-\theta \right)=\tan(\theta )}
sec
(
π
/
2
−
θ
)
=
csc
(
θ
)
{\displaystyle \sec \left(\pi /2-\theta \right)=\csc(\theta )}
csc
(
π
/
2
−
θ
)
=
sec
(
θ
)
{\displaystyle \csc \left(\pi /2-\theta \right)=\sec(\theta )}
Identidade 1 :
sin
2
(
x
)
+
cos
2
(
x
)
=
1
{\displaystyle \sin ^{2}(x)+\cos ^{2}(x)=1}
Os dois resultados a seguir seguem desta e das identidades de proporção. Para obter o primeiro, dividir ambos os lados de
sin
2
(
x
)
+
cos
2
(
x
)
=
1
{\displaystyle \sin ^{2}(x)+\cos ^{2}(x)=1}
cos
2
(
x
)
{\displaystyle \cos ^{2}(x)}
sin
2
(
x
)
{\displaystyle \sin ^{2}(x)}
tan
2
(
x
)
+
1
=
sec
2
(
x
)
{\displaystyle \tan ^{2}(x)+1\ =\sec ^{2}(x)}
1
+
cot
2
(
x
)
=
csc
2
(
x
)
{\displaystyle 1\ +\cot ^{2}(x)=\csc ^{2}(x)}
Similarmente
1
+
cot
2
(
x
)
=
csc
2
(
x
)
{\displaystyle 1\ +\cot ^{2}(x)=\csc ^{2}(x)}
csc
2
(
x
)
−
cot
2
(
x
)
=
1
{\displaystyle \csc ^{2}(x)-\cot ^{2}(x)=1}
Identidade 2 :
A identidade seguinte envolve todas as três funções recíprocas.
csc
2
(
x
)
+
sec
2
(
x
)
−
cot
2
(
x
)
=
2
+
tan
2
(
x
)
{\displaystyle \csc ^{2}(x)+\sec ^{2}(x)-\cot ^{2}(x)=2\ +\tan ^{2}(x)}
Prova 2:
Considerar o diagrama do triângulo acima. Notar que
a
2
+
b
2
=
h
2
{\displaystyle a^{2}+b^{2}=h^{2}}
teorema de Pitágoras .
csc
2
(
x
)
+
sec
2
(
x
)
=
h
2
a
2
+
h
2
b
2
=
a
2
+
b
2
a
2
+
a
2
+
b
2
b
2
=
2
+
b
2
a
2
+
a
2
b
2
{\displaystyle \csc ^{2}(x)+\sec ^{2}(x)={\frac {h^{2}}{a^{2}}}+{\frac {h^{2}}{b^{2}}}={\frac {a^{2}+b^{2}}{a^{2}}}+{\frac {a^{2}+b^{2}}{b^{2}}}=2\ +{\frac {b^{2}}{a^{2}}}+{\frac {a^{2}}{b^{2}}}}
Substituindo com funções apropriadas
2
+
b
2
a
2
+
a
2
b
2
=
2
+
tan
2
(
x
)
+
cot
2
(
x
)
{\displaystyle 2\ +{\frac {b^{2}}{a^{2}}}+{\frac {a^{2}}{b^{2}}}=2\ +\tan ^{2}(x)+\cot ^{2}(x)}
Rearranjando resulta:
csc
2
(
x
)
+
sec
2
(
x
)
−
cot
2
(
x
)
=
2
+
tan
2
(
x
)
{\displaystyle \csc ^{2}(x)+\sec ^{2}(x)-\cot ^{2}(x)=2\ +\tan ^{2}(x)}
Ilustração da fórmula da soma. Desenhar uma linha horizontal (o eixo x ); marcar uma origem O. Desenhar uma linha de O com um ângulo
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
x é
α
+
β
{\displaystyle \alpha +\beta }
Colocar P na linha definida por
α
+
β
{\displaystyle \alpha +\beta }
Seja PQ uma linha perpendicular à linha OQ definida pelo ângulo
α
{\displaystyle \alpha }
∴
{\displaystyle \therefore }
Seja QA uma perpendicular do ponto A no eixo x para Q e seja PB uma perpendicular do ponto B no eixo x até P.
∴
{\displaystyle \therefore }
Desenhar R em PB tal que QR seja paralelo ao eixo x .
Agora o ângulo
R
P
Q
=
α
{\displaystyle RPQ=\alpha }
O
Q
A
=
π
2
−
α
{\displaystyle OQA={\frac {\pi }{2}}-\alpha }
R
Q
O
=
α
,
R
Q
P
=
π
2
−
α
{\displaystyle RQO=\alpha ,RQP={\frac {\pi }{2}}-\alpha }
R
P
Q
=
α
{\displaystyle RPQ=\alpha }
R
P
Q
=
π
2
−
R
Q
P
=
π
2
−
(
π
2
−
R
Q
O
)
=
R
Q
O
=
α
{\displaystyle RPQ={\tfrac {\pi }{2}}-RQP={\tfrac {\pi }{2}}-({\tfrac {\pi }{2}}-RQO)=RQO=\alpha }
O
P
=
1
{\displaystyle OP=1}
P
Q
=
sin
(
β
)
{\displaystyle PQ=\sin(\beta )}
O
Q
=
cos
(
β
)
{\displaystyle OQ=\cos(\beta )}
A
Q
O
Q
=
sin
(
α
)
{\displaystyle {\frac {AQ}{OQ}}=\sin(\alpha )}
A
Q
=
sin
(
α
)
cos
(
β
)
{\displaystyle AQ=\sin(\alpha )\cos(\beta )}
P
R
P
Q
=
cos
(
α
)
{\displaystyle {\frac {PR}{PQ}}=\cos(\alpha )}
P
R
=
cos
(
α
)
sin
(
β
)
{\displaystyle PR=\cos(\alpha )\sin(\beta )}
sin
(
α
+
β
)
=
P
B
=
R
B
+
P
R
=
A
Q
+
P
R
=
sin
(
α
)
cos
(
β
)
+
cos
(
α
)
sin
(
β
)
{\displaystyle \sin(\alpha +\beta )=PB=RB+PR=AQ+PR=\sin(\alpha )\cos(\beta )+\cos(\alpha )\sin(\beta )}
Substituindo
−
β
{\displaystyle -\beta }
β
{\displaystyle \beta }
sin
(
α
−
β
)
=
sin
(
α
)
cos
(
−
β
)
+
cos
(
α
)
sin
(
−
β
)
{\displaystyle \sin(\alpha -\beta )=\sin(\alpha )\cos(-\beta )+\cos(\alpha )\sin(-\beta )}
sin
(
α
−
β
)
=
sin
(
α
)
cos
(
β
)
−
cos
(
α
)
sin
(
β
)
{\displaystyle \sin(\alpha -\beta )=\sin(\alpha )\cos(\beta )-\cos(\alpha )\sin(\beta )}
Outra prova rigorosa, e bem mais simples, pode ser obtida usando a fórmula de Euler , conhecida da análise complexa. A fórmula de Euler estabelece que
e
i
φ
=
cos
(
φ
)
+
i
sin
(
φ
)
{\displaystyle e^{i\varphi }=\cos(\varphi )+i\sin(\varphi )}
Segue que para ângulos
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
e
i
(
α
+
β
)
=
cos
(
α
+
β
)
+
i
sin
(
α
+
β
)
{\displaystyle e^{i(\alpha +\beta )}=\cos(\alpha +\beta )+i\sin(\alpha +\beta )}
Também, usando as seguintes propriedades de funções exponenciais:
e
i
(
α
+
β
)
=
e
i
α
e
i
β
=
(
cos
(
α
)
+
i
sin
(
α
)
)
(
cos
(
β
)
+
i
sin
(
β
)
)
{\displaystyle e^{i(\alpha +\beta )}=e^{i\alpha }e^{i\beta }=(\cos(\alpha )+i\sin(\alpha ))(\cos(\beta )+i\sin(\beta ))}
Manipulando o produto:
e
i
(
α
+
β
)
=
(
cos
(
α
)
cos
(
β
)
−
sin
(
α
)
sin
(
β
)
)
+
i
(
sin
(
α
)
cos
(
β
)
+
sin
(
β
)
cos
(
α
)
)
{\displaystyle e^{i(\alpha +\beta )}=(\cos(\alpha )\cos(\beta )-\sin(\alpha )\sin(\beta ))+i(\sin(\alpha )\cos(\beta )+\sin(\beta )\cos(\alpha ))}
Igualando as partes real e imaginária:
cos
(
α
+
β
)
=
cos
(
α
)
cos
(
β
)
−
sin
(
α
)
sin
(
β
)
{\displaystyle \cos(\alpha +\beta )=\cos(\alpha )\cos(\beta )-\sin(\alpha )\sin(\beta )}
sin
(
α
+
β
)
=
sin
(
α
)
cos
(
β
)
+
sin
(
β
)
cos
(
α
)
{\displaystyle \sin(\alpha +\beta )=\sin(\alpha )\cos(\beta )+\sin(\beta )\cos(\alpha )}
Observando a figura acima,
O
P
=
1
{\displaystyle OP=1}
P
Q
=
sin
(
β
)
{\displaystyle PQ=\sin(\beta )}
O
Q
=
cos
(
β
)
{\displaystyle OQ=\cos(\beta )}
O
A
O
Q
=
cos
(
α
)
{\displaystyle {\frac {OA}{OQ}}=\cos(\alpha )}
O
A
=
cos
(
α
)
cos
(
β
)
{\displaystyle OA=\cos(\alpha )\cos(\beta )}
R
Q
P
Q
=
sin
(
α
)
{\displaystyle {\frac {RQ}{PQ}}=\sin(\alpha )}
R
Q
=
sin
(
α
)
sin
(
β
)
{\displaystyle RQ=\sin(\alpha )\sin(\beta )}
cos
(
α
+
β
)
=
O
B
=
O
A
−
B
A
=
O
A
−
R
Q
=
cos
(
α
)
cos
(
β
)
−
sin
(
α
)
sin
(
β
)
{\displaystyle \cos(\alpha +\beta )=OB=OA-BA=OA-RQ=\cos(\alpha )\cos(\beta )\ -\sin(\alpha )\sin(\beta )}
Substituindo
−
β
{\displaystyle -\beta }
β
{\displaystyle \beta }
cos
(
α
−
β
)
=
cos
(
α
)
cos
(
−
β
)
−
sin
(
α
)
sin
(
−
β
)
,
{\displaystyle \cos(\alpha -\beta )=\cos(\alpha )\cos(-\beta )-\sin(\alpha )\sin(-\beta ),}
cos
(
α
−
β
)
=
cos
(
α
)
cos
(
β
)
+
sin
(
α
)
sin
(
β
)
{\displaystyle \cos(\alpha -\beta )=\cos(\alpha )\cos(\beta )+\sin(\alpha )\sin(\beta )}
Usando as fórmulas para ângulos complementares,
cos
(
α
+
β
)
=
sin
(
π
/
2
−
(
α
+
β
)
)
=
sin
(
(
π
/
2
−
α
)
−
β
)
=
sin
(
π
/
2
−
α
)
cos
(
β
)
−
cos
(
π
/
2
−
α
)
sin
(
β
)
=
cos
(
α
)
cos
(
β
)
−
sin
(
α
)
sin
(
β
)
{\displaystyle {\begin{aligned}\cos(\alpha +\beta )&=\sin \left(\pi /2-(\alpha +\beta )\right)\\&=\sin \left((\pi /2-\alpha )-\beta \right)\\&=\sin \left(\pi /2-\alpha \right)\cos(\beta )-\cos \left(\pi /2-\alpha \right)\sin(\beta )\\&=\cos(\alpha )\cos(\beta )-\sin(\alpha )\sin(\beta )\\\end{aligned}}}
Das fórmulas para seno e cosseno resulta
tan
(
α
+
β
)
=
sin
(
α
+
β
)
cos
(
α
+
β
)
=
sin
(
α
)
cos
(
β
)
+
cos
(
α
)
sin
(
β
)
cos
(
α
)
cos
(
β
)
−
sin
(
α
)
sin
(
β
)
{\displaystyle \tan(\alpha +\beta )={\frac {\sin(\alpha +\beta )}{\cos(\alpha +\beta )}}={\frac {\sin(\alpha )\cos(\beta )+\cos(\alpha )\sin(\beta )}{\cos(\alpha )\cos(\beta )-\sin(\alpha )\sin(\beta )}}}
Dividindo numerador e denominador por
cos
(
α
)
cos
(
β
)
{\displaystyle \cos(\alpha )\cos(\beta )}
tan
(
α
+
β
)
=
tan
(
α
)
+
tan
(
β
)
1
−
tan
(
α
)
tan
(
β
)
{\displaystyle \tan(\alpha +\beta )={\frac {\tan(\alpha )+\tan(\beta )}{1-\tan(\alpha )\tan(\beta )}}}
Subtraindo
β
{\displaystyle \beta }
α
{\displaystyle \alpha }
tan
(
−
β
)
=
−
tan
(
β
)
{\displaystyle \tan(-\beta )=-\tan(\beta )}
tan
(
α
−
β
)
=
tan
(
α
)
+
tan
(
−
β
)
1
−
tan
(
α
)
tan
(
−
β
)
=
tan
(
α
)
−
tan
(
β
)
1
+
tan
(
α
)
tan
(
β
)
{\displaystyle \tan(\alpha -\beta )={\frac {\tan(\alpha )+\tan(-\beta )}{1-\tan(\alpha )\tan(-\beta )}}={\frac {\tan(\alpha )-\tan(\beta )}{1+\tan(\alpha )\tan(\beta )}}}
Similarmente, das fórmulas para seno e cosseno resulta
cot
(
α
+
β
)
=
cos
(
α
+
β
)
sin
(
α
+
β
)
=
cos
(
α
)
cos
(
β
)
−
sin
(
α
)
sin
(
β
)
sin
(
α
)
cos
(
β
)
+
cos
(
α
)
sin
(
β
)
{\displaystyle \cot(\alpha +\beta )={\frac {\cos(\alpha +\beta )}{\sin(\alpha +\beta )}}={\frac {\cos(\alpha )\cos(\beta )-\sin(\alpha )\sin(\beta )}{\sin(\alpha )\cos(\beta )+\cos(\alpha )\sin(\beta )}}}
Dividindo então numerador e denominador por
sin
(
α
)
sin
(
β
)
{\displaystyle \sin(\alpha )\sin(\beta )}
cot
(
α
+
β
)
=
cot
(
α
)
cot
(
β
)
−
1
cot
(
α
)
+
cot
(
β
)
{\displaystyle \cot(\alpha +\beta )={\frac {\cot(\alpha )\cot(\beta )-1}{\cot(\alpha )+\cot(\beta )}}}
Ou, usando
cot
(
θ
)
=
1
tan
(
θ
)
{\displaystyle \cot(\theta )={\frac {1}{\tan(\theta )}}}
cot
(
α
+
β
)
=
1
−
tan
(
α
)
tan
(
β
)
tan
(
α
)
+
tan
(
β
)
=
1
tan
(
α
)
tan
(
β
)
−
1
1
tan
(
α
)
+
1
tan
(
β
)
=
cot
(
α
)
cot
(
β
)
−
1
cot
(
α
)
+
cot
(
β
)
{\displaystyle \cot(\alpha +\beta )={\frac {1-\tan(\alpha )\tan(\beta )}{\tan(\alpha )+\tan(\beta )}}={\frac {{\frac {1}{\tan(\alpha )\tan(\beta )}}-1}{{\frac {1}{\tan(\alpha )}}+{\frac {1}{\tan(\beta )}}}}={\frac {\cot(\alpha )\cot(\beta )-1}{\cot(\alpha )+\cot(\beta )}}}
Usando
cot
(
−
β
)
=
−
cot
(
β
)
{\displaystyle \cot(-\beta )=-\cot(\beta )}
cot
(
α
−
β
)
=
cot
(
α
)
cot
(
−
β
)
−
1
cot
(
α
)
+
cot
(
−
β
)
=
cot
(
α
)
cot
(
β
)
+
1
cot
(
β
)
−
cot
(
α
)
{\displaystyle \cot(\alpha -\beta )={\frac {\cot(\alpha )\cot(-\beta )-1}{\cot(\alpha )+\cot(-\beta )}}={\frac {\cot(\alpha )\cot(\beta )+1}{\cot(\beta )-\cot(\alpha )}}}
Das identidades para soma de ângulos resulta
sin
(
2
θ
)
=
2
sin
(
θ
)
cos
(
θ
)
{\displaystyle \sin(2\theta )=2\sin(\theta )\cos(\theta )}
e
cos
(
2
θ
)
=
cos
2
(
θ
)
−
sin
2
(
θ
)
{\displaystyle \cos(2\theta )=\cos ^{2}(\theta )-\sin ^{2}(\theta )}
As identidades pitagóricas dão as duas formas alternativas para a último destes:
cos
(
2
θ
)
=
2
cos
2
(
θ
)
−
1
{\displaystyle \cos(2\theta )=2\cos ^{2}(\theta )-1}
cos
(
2
θ
)
=
1
−
2
sin
2
(
θ
)
{\displaystyle \cos(2\theta )=1-2\sin ^{2}(\theta )}
As identidades de soma dos ângulos também fornecem
tan
(
2
θ
)
=
2
tan
(
θ
)
1
−
tan
2
θ
=
2
cot
(
θ
)
−
tan
(
θ
)
{\displaystyle \tan(2\theta )={\frac {2\tan(\theta )}{1-\tan ^{2}\theta }}={\frac {2}{\cot(\theta )-\tan(\theta )}}}
cot
(
2
θ
)
=
cot
2
θ
−
1
2
cot
(
θ
)
=
cot
(
θ
)
−
tan
(
θ
)
2
{\displaystyle \cot(2\theta )={\frac {\cot ^{2}\theta -1}{2\cot(\theta )}}={\frac {\cot(\theta )-\tan(\theta )}{2}}}
Também pode ser provado usando a fórmula de Euler
e
i
φ
=
cos
(
φ
)
+
i
sin
(
φ
)
{\displaystyle e^{i\varphi }=\cos(\varphi )+i\sin(\varphi )}
Elevando ambos os lados ao quadrado
e
i
2
φ
=
(
cos
(
φ
)
+
i
sin
(
φ
)
)
2
{\displaystyle e^{i2\varphi }=(\cos(\varphi )+i\sin(\varphi ))^{2}}
Substituindo o ângulo pela sua versão dupla, que fornece o mesmo resultado no lado esquerdo da equação, resulta
e
i
2
φ
=
cos
(
2
φ
)
+
i
sin
(
2
φ
)
{\displaystyle e^{i2\varphi }=\cos(2\varphi )+i\sin(2\varphi )}
Segue que
(
cos
(
φ
)
+
i
sin
(
φ
)
)
2
=
cos
(
2
φ
)
+
i
sin
(
2
φ
)
{\displaystyle (\cos(\varphi )+i\sin(\varphi ))^{2}=\cos(2\varphi )+i\sin(2\varphi )}
Expandindo o quadrado e simplificando no lado esquerdo da equação resulta
i
(
2
sin
(
φ
)
cos
(
φ
)
)
+
cos
2
(
φ
)
−
sin
2
(
φ
)
=
cos
(
2
φ
)
+
i
sin
(
2
φ
)
{\displaystyle i(2\sin(\varphi )\cos(\varphi ))+\cos ^{2}(\varphi )-\sin ^{2}(\varphi )\ =\cos(2\varphi )+i\sin(2\varphi )}
Como as partes real e imaginária da equação devem ser iguais, resulta
cos
2
(
φ
)
−
sin
2
(
φ
)
=
cos
(
2
φ
)
{\displaystyle \cos ^{2}(\varphi )-\sin ^{2}(\varphi )\ =\cos(2\varphi )}
e
2
sin
(
φ
)
cos
(
φ
)
=
sin
(
2
φ
)
{\displaystyle 2\sin(\varphi )\cos(\varphi )=\sin(2\varphi )}
As duas identidades que fornecem as formas alternativas para cos(2θ) levam às seguintes equações:
cos
(
θ
2
)
=
±
1
+
cos
(
θ
)
2
,
{\displaystyle \cos \left({\frac {\theta }{2}}\right)=\pm \,{\sqrt {\frac {1+\cos(\theta )}{2}}},}
sin
(
θ
2
)
=
±
1
−
cos
(
θ
)
2
.
{\displaystyle \sin \left({\frac {\theta }{2}}\right)=\pm \,{\sqrt {\frac {1-\cos(\theta )}{2}}}.}
O sinal da raiz quadrada deve ser escolhido adequadamente—notar que se 2π é adicionado a θ, as quantidades na raiz quadrada não são alteradas, mas os lados esquerdos das equações mudam de sinal. Assim, o sinal correto a usar depende do valor de θ.
Para a função tangente a equação é:
tan
(
θ
2
)
=
±
1
−
cos
(
θ
)
1
+
cos
(
θ
)
.
{\displaystyle \tan \left({\frac {\theta }{2}}\right)=\pm \,{\sqrt {\frac {1-\cos(\theta )}{1+\cos(\theta )}}}.}
Multiplicando então o numerador e o denominador dentro da raiz quadrada por (1 + cos(θ)) e usando identidades pitagóricas leva a
tan
(
θ
2
)
=
sin
(
θ
)
1
+
cos
(
θ
)
.
{\displaystyle \tan \left({\frac {\theta }{2}}\right)={\frac {\sin(\theta )}{1+\cos(\theta )}}.}
Além disso, se o numerador e o denominador forem ambos multiplicados por (1 - cos(θ)), o resultado é
tan
(
θ
2
)
=
1
−
cos
(
θ
)
sin
(
θ
)
.
{\displaystyle \tan \left({\frac {\theta }{2}}\right)={\frac {1-\cos(\theta )}{\sin(\theta )}}.}
Isso também fornece
tan
(
θ
2
)
=
csc
(
θ
)
−
cot
(
θ
)
.
{\displaystyle \tan \left({\frac {\theta }{2}}\right)=\csc(\theta )-\cot(\theta ).}
Manipulações similares para a função cot fornecem
cot
(
θ
2
)
=
±
1
+
cos
(
θ
)
1
−
cos
(
θ
)
=
1
+
cos
(
θ
)
sin
(
θ
)
=
sin
(
θ
)
1
−
cos
(
θ
)
=
csc
(
θ
)
+
cot
(
θ
)
.
{\displaystyle \cot \left({\frac {\theta }{2}}\right)=\pm \,{\sqrt {\frac {1+\cos(\theta )}{1-\cos(\theta )}}}={\frac {1+\cos(\theta )}{\sin(\theta )}}={\frac {\sin(\theta )}{1-\cos(\theta )}}=\csc(\theta )+\cot(\theta ).}
Se
ψ
+
θ
+
ϕ
=
π
=
{\displaystyle \psi +\theta +\phi =\pi =}
ψ
{\displaystyle \psi }
θ
{\displaystyle \theta }
ϕ
{\displaystyle \phi }
tan
(
ψ
)
+
tan
(
θ
)
+
tan
(
ϕ
)
=
tan
(
ψ
)
tan
(
θ
)
tan
(
ϕ
)
.
{\displaystyle \tan(\psi )+\tan(\theta )+\tan(\phi )=\tan(\psi )\tan(\theta )\tan(\phi ).}
Prova:[ 1]
ψ
=
π
−
θ
−
ϕ
tan
(
ψ
)
=
tan
(
π
−
θ
−
ϕ
)
=
−
tan
(
θ
+
ϕ
)
=
−
tan
(
θ
)
−
tan
(
ϕ
)
1
−
tan
(
θ
)
tan
(
ϕ
)
=
tan
(
θ
)
+
tan
(
ϕ
)
tan
(
θ
)
tan
(
ϕ
)
−
1
(
tan
(
θ
)
tan
(
ϕ
)
−
1
)
tan
(
ψ
)
=
tan
(
θ
)
+
tan
(
ϕ
)
tan
(
ψ
)
tan
(
θ
)
tan
(
ϕ
)
−
tan
(
ψ
)
=
tan
(
θ
)
+
tan
(
ϕ
)
tan
(
ψ
)
tan
(
θ
)
tan
(
ϕ
)
=
tan
(
ψ
)
+
tan
(
θ
)
+
tan
(
ϕ
)
{\displaystyle {\begin{aligned}\psi &=\pi -\theta -\phi \\\tan(\psi )&=\tan(\pi -\theta -\phi )\\&=-\tan(\theta +\phi )\\&={\frac {-\tan(\theta )-\tan(\phi )}{1-\tan(\theta )\tan(\phi )}}\\&={\frac {\tan(\theta )+\tan(\phi )}{\tan(\theta )\tan(\phi )-1}}\\(\tan(\theta )\tan(\phi )-1)\tan(\psi )&=\tan(\theta )+\tan(\phi )\\\tan(\psi )\tan(\theta )\tan(\phi )-\tan(\psi )&=\tan(\theta )+\tan(\phi )\\\tan(\psi )\tan(\theta )\tan(\phi )&=\tan(\psi )+\tan(\theta )+\tan(\phi )\\\end{aligned}}}
Se
ψ
+
θ
+
ϕ
=
π
2
=
{\displaystyle \psi +\theta +\phi ={\tfrac {\pi }{2}}=}
cot
(
ψ
)
+
cot
(
θ
)
+
cot
(
ϕ
)
=
cot
(
ψ
)
cot
(
θ
)
cot
(
ϕ
)
{\displaystyle \cot(\psi )+\cot(\theta )+\cot(\phi )=\cot(\psi )\cot(\theta )\cot(\phi )}
Prova:
Substituir cada um dos
ψ
{\displaystyle \psi }
θ
{\displaystyle \theta }
ϕ
{\displaystyle \phi }
Dado
ψ
+
θ
+
ϕ
=
π
2
{\displaystyle \psi +\theta +\phi ={\tfrac {\pi }{2}}}
∴
(
π
2
−
ψ
)
+
(
π
2
−
θ
)
+
(
π
2
−
ϕ
)
=
3
π
2
−
(
ψ
+
θ
+
ϕ
)
=
3
π
2
−
π
2
=
π
{\displaystyle \therefore ({\tfrac {\pi }{2}}-\psi )+({\tfrac {\pi }{2}}-\theta )+({\tfrac {\pi }{2}}-\phi )={\tfrac {3\pi }{2}}-(\psi +\theta +\phi )={\tfrac {3\pi }{2}}-{\tfrac {\pi }{2}}=\pi }
então o resultado segue da identidade da tripla tangente.
sin
(
θ
)
±
cos
(
ϕ
)
=
2
sin
(
θ
±
ϕ
2
)
cos
(
θ
∓
ϕ
2
)
{\displaystyle \sin(\theta )\pm \cos(\phi )=2\sin \left({\frac {\theta \pm \phi }{2}}\right)\cos \left({\frac {\theta \mp \phi }{2}}\right)}
cos
(
θ
)
+
cos
(
ϕ
)
=
2
cos
(
θ
+
ϕ
2
)
cos
(
θ
−
ϕ
2
)
{\displaystyle \cos(\theta )+\cos(\phi )=2\cos \left({\frac {\theta +\phi }{2}}\right)\cos \left({\frac {\theta -\phi }{2}}\right)}
cos
(
θ
)
−
cos
(
ϕ
)
=
−
2
sin
(
θ
+
ϕ
2
)
sin
(
θ
−
ϕ
2
)
{\displaystyle \cos(\theta )-\cos(\phi )=-2\sin \left({\frac {\theta +\phi }{2}}\right)\sin \left({\frac {\theta -\phi }{2}}\right)}
Iniciar com as identidades da soma de ângulos
sin
(
α
+
β
)
=
sin
(
α
)
cos
(
β
)
+
cos
(
α
)
sin
(
β
)
{\displaystyle \sin(\alpha +\beta )=\sin(\alpha )\cos(\beta )+\cos(\alpha )\sin(\beta )}
sin
(
α
−
β
)
=
sin
(
α
)
cos
(
β
)
−
cos
(
α
)
sin
(
β
)
{\displaystyle \sin(\alpha -\beta )=\sin(\alpha )\cos(\beta )-\cos(\alpha )\sin(\beta )}
Adicionando ambas resulta
sin
(
α
+
β
)
+
sin
(
α
−
β
)
=
sin
(
α
)
cos
(
β
)
+
cos
(
α
)
sin
(
β
)
+
sin
(
α
)
cos
(
β
)
−
cos
(
α
)
sin
(
β
)
=
2
sin
(
α
)
cos
(
β
)
{\displaystyle \sin(\alpha +\beta )+\sin(\alpha -\beta )=\sin(\alpha )\cos(\beta )+\cos(\alpha )\sin(\beta )+\sin(\alpha )\cos(\beta )-\cos(\alpha )\sin(\beta )=2\sin(\alpha )\cos(\beta )}
Similarmente, subtraindo as duas identidades de soma de ângulos
sin
(
α
+
β
)
−
sin
(
α
−
β
)
=
sin
(
α
)
cos
(
β
)
+
cos
(
α
)
sin
(
β
)
−
sin
(
α
)
cos
(
β
)
+
cos
(
α
)
sin
(
β
)
=
2
cos
(
α
)
sin
(
β
)
{\displaystyle \sin(\alpha +\beta )-\sin(\alpha -\beta )=\sin(\alpha )\cos(\beta )+\cos(\alpha )\sin(\beta )-\sin(\alpha )\cos(\beta )+\cos(\alpha )\sin(\beta )=2\cos(\alpha )\sin(\beta )}
Sejam
α
+
β
=
θ
{\displaystyle \alpha +\beta =\theta }
α
−
β
=
ϕ
{\displaystyle \alpha -\beta =\phi }
∴
α
=
θ
+
ϕ
2
{\displaystyle \therefore \alpha ={\frac {\theta +\phi }{2}}}
β
=
θ
−
ϕ
2
{\displaystyle \beta ={\frac {\theta -\phi }{2}}}
Substituindo
θ
{\displaystyle \theta }
ϕ
{\displaystyle \phi }
sin
(
θ
)
+
cos
(
ϕ
)
=
2
sin
(
θ
+
ϕ
2
)
cos
(
θ
−
ϕ
2
)
{\displaystyle \sin(\theta )+\cos(\phi )=2\sin \left({\frac {\theta +\phi }{2}}\right)\cos \left({\frac {\theta -\phi }{2}}\right)}
sin
(
θ
)
−
cos
(
ϕ
)
=
2
cos
(
θ
+
ϕ
2
)
sin
(
θ
−
ϕ
2
)
=
2
sin
(
θ
−
ϕ
2
)
cos
(
θ
+
ϕ
2
)
{\displaystyle \sin(\theta )-\cos(\phi )=2\cos \left({\frac {\theta +\phi }{2}}\right)\sin \left({\frac {\theta -\phi }{2}}\right)=2\sin \left({\frac {\theta -\phi }{2}}\right)\cos \left({\frac {\theta +\phi }{2}}\right)}
Portanto,
sin
(
θ
)
±
cos
(
ϕ
)
=
2
sin
(
θ
±
ϕ
2
)
cos
(
θ
∓
ϕ
2
)
{\displaystyle \sin(\theta )\pm \cos(\phi )=2\sin \left({\frac {\theta \pm \phi }{2}}\right)\cos \left({\frac {\theta \mp \phi }{2}}\right)}
Similarmente para cossenos, começando com as identidades de soma de ângulos
cos
(
α
+
β
)
=
cos
(
α
)
cos
(
β
)
−
sin
(
α
)
sin
(
β
)
{\displaystyle \cos(\alpha +\beta )=\cos(\alpha )\cos(\beta )\ -\sin(\alpha )\sin(\beta )}
cos
(
α
−
β
)
=
cos
(
α
)
cos
(
β
)
+
sin
(
α
)
sin
(
β
)
{\displaystyle \cos(\alpha -\beta )=\cos(\alpha )\cos(\beta )+\sin(\alpha )\sin(\beta )}
Novamente, adicionando e subtraindo
cos
(
α
+
β
)
+
cos
(
α
−
β
)
=
cos
(
α
)
cos
(
β
)
−
sin
(
α
)
sin
(
β
)
+
cos
(
α
)
cos
(
β
)
+
sin
(
α
)
sin
(
β
)
=
2
cos
(
α
)
cos
(
β
)
{\displaystyle \cos(\alpha +\beta )+\cos(\alpha -\beta )=\cos(\alpha )\cos(\beta )\ -\sin(\alpha )\sin(\beta )+\cos(\alpha )\cos(\beta )+\sin(\alpha )\sin(\beta )=2\cos(\alpha )\cos(\beta )}
cos
(
α
+
β
)
−
cos
(
α
−
β
)
=
cos
(
α
)
cos
(
β
)
−
sin
(
α
)
sin
(
β
)
−
cos
(
α
)
cos
(
β
)
−
sin
(
α
)
sin
(
β
)
=
−
2
sin
(
α
)
sin
(
β
)
{\displaystyle \cos(\alpha +\beta )-\cos(\alpha -\beta )=\cos(\alpha )\cos(\beta )\ -\sin(\alpha )\sin(\beta )-\cos(\alpha )\cos(\beta )-\sin(\alpha )\sin(\beta )=-2\sin(\alpha )\sin(\beta )}
Substituindo
θ
{\displaystyle \theta }
ϕ
{\displaystyle \phi }
cos
(
θ
)
+
cos
(
ϕ
)
=
2
cos
(
θ
+
ϕ
2
)
cos
(
θ
−
ϕ
2
)
{\displaystyle \cos(\theta )+\cos(\phi )=2\cos \left({\frac {\theta +\phi }{2}}\right)\cos \left({\frac {\theta -\phi }{2}}\right)}
cos
(
θ
)
−
cos
(
ϕ
)
=
−
2
sin
(
θ
+
ϕ
2
)
sin
(
θ
−
ϕ
2
)
{\displaystyle \cos(\theta )-\cos(\phi )=-2\sin \left({\frac {\theta +\phi }{2}}\right)\sin \left({\frac {\theta -\phi }{2}}\right)}
Ilustração das desigualdades seno e tangente. A figura na direita mostra um setor de um círculo com raio 1. O setor é θ /(2π )θ /2θ < π /2
O
A
=
O
D
=
1
{\displaystyle OA=OD=1}
A
B
=
sin
(
θ
)
{\displaystyle AB=\sin(\theta )}
C
D
=
tan
(
θ
)
{\displaystyle CD=\tan(\theta )}
A área do triângulo OAD AB /2sin(θ )/2 . A área do triângulo OCD CD /2tan(θ )/2 .
Como o triângulo OAD OCD
sin
(
θ
)
<
θ
<
tan
(
θ
)
.
{\displaystyle \sin(\theta )<\theta <\tan(\theta ).}
Este argumento geométrico baseia-se nas definições de comprimento do arco e área, que atuam como premissas, portanto é mais uma condição imposta na construção de funções trigonométricas do que uma propriedade comprovável.[ 2] θ > π /2θ > 1sin θ ≤ 1 (por causa da identidade pitagórica), então sin θ < θ . Temos então
sin
(
θ
)
θ
<
1
i
f
0
<
θ
.
{\displaystyle {\frac {\sin(\theta )}{\theta }}<1\ \ \ \mathrm {if} \ \ \ 0<\theta .}
Para valores negativos de θ
sin
(
θ
)
θ
=
sin
(
−
θ
)
−
θ
<
1.
{\displaystyle {\frac {\sin(\theta )}{\theta }}={\frac {\sin(-\theta )}{-\theta }}<1.}
Então
sin
(
θ
)
θ
<
1
se
θ
≠
0
,
{\displaystyle {\frac {\sin(\theta )}{\theta }}<1\quad {\text{se }}\quad \theta \neq 0,}
e
tan
(
θ
)
θ
>
1
se
0
<
θ
<
π
2
.
{\displaystyle {\frac {\tan(\theta )}{\theta }}>1\quad {\text{se }}\quad 0<\theta <{\frac {\pi }{2}}.}
lim
θ
→
0
sin
(
θ
)
=
0
{\displaystyle \lim _{\theta \to 0}{\sin(\theta )}=0}
lim
θ
→
0
cos
(
θ
)
=
1
{\displaystyle \lim _{\theta \to 0}{\cos(\theta )}=1}
lim
θ
→
0
sin
(
θ
)
θ
=
1.
{\displaystyle \lim _{\theta \to 0}{\frac {\sin(\theta )}{\theta }}=1.}
Em outras palavras, a função seno é diferenciável em 0, e sua derivada é 1.
Prova: Das desigualdades prévias temos, para ângulos pequenos,
sin
(
θ
)
<
θ
<
tan
(
θ
)
{\displaystyle \sin(\theta )<\theta <\tan(\theta )}
e portanto
sin
(
θ
)
θ
<
1
<
tan
(
θ
)
θ
{\displaystyle {\frac {\sin(\theta )}{\theta }}<1<{\frac {\tan(\theta )}{\theta }}}
e consideremos a desigualdade do lado direito. Como
tan
(
θ
)
=
sin
(
θ
)
cos
(
θ
)
{\displaystyle \tan(\theta )={\frac {\sin(\theta )}{\cos(\theta )}}}
∴
1
<
sin
(
θ
)
θ
cos
(
θ
)
.
{\displaystyle \therefore 1<{\frac {\sin(\theta )}{\theta \cos(\theta )}}.}
Multiplicando por
cos
(
θ
)
{\displaystyle \cos(\theta )}
cos
(
θ
)
<
sin
(
θ
)
θ
.
{\displaystyle \cos(\theta )<{\frac {\sin(\theta )}{\theta }}.}
Combinando com a desigualdade do lado esquerdo:
cos
(
θ
)
<
sin
(
θ
)
θ
<
1.
{\displaystyle \cos(\theta )<{\frac {\sin(\theta )}{\theta }}<1.}
Tomando
cos
(
θ
)
{\displaystyle \cos(\theta )}
θ
→
0
{\displaystyle \theta \to 0}
lim
θ
→
0
cos
(
θ
)
=
1.
{\displaystyle \lim _{\theta \to 0}{\cos(\theta )}=1.}
Portanto,
lim
θ
→
0
sin
(
θ
)
θ
=
1
{\displaystyle \lim _{\theta \to 0}{\frac {\sin(\theta )}{\theta }}=1}
lim
θ
→
0
1
−
cos
(
θ
)
θ
=
0
{\displaystyle \lim _{\theta \to 0}{\frac {1-\cos(\theta )}{\theta }}=0}
Prova:
1
−
cos
(
θ
)
θ
=
1
−
cos
2
(
θ
)
θ
(
1
+
cos
(
θ
)
)
=
sin
2
(
θ
)
θ
(
1
+
cos
(
θ
)
)
=
(
sin
(
θ
)
θ
)
×
sin
(
θ
)
×
(
1
1
+
cos
(
θ
)
)
{\displaystyle {\begin{aligned}{\frac {1-\cos(\theta )}{\theta }}&={\frac {1-\cos ^{2}(\theta )}{\theta (1+\cos(\theta ))}}\\&={\frac {\sin ^{2}(\theta )}{\theta (1+\cos(\theta ))}}\\&=\left({\frac {\sin(\theta )}{\theta }}\right)\times \sin(\theta )\times \left({\frac {1}{1+\cos(\theta )}}\right)\\\end{aligned}}}
Os limites destas três quantidades são 1, 0 e 1/2, então o limite resultante é zero.
Identidade da razão cosseno e quadrado do ângulo [ editar | editar código-fonte ]
lim
θ
→
0
1
−
cos
(
θ
)
θ
2
=
1
2
{\displaystyle \lim _{\theta \to 0}{\frac {1-\cos(\theta )}{\theta ^{2}}}={\frac {1}{2}}}
Prova:
Como na prova precedente,
1
−
cos
(
θ
)
θ
2
=
sin
(
θ
)
θ
×
sin
(
θ
)
θ
×
1
1
+
cos
(
θ
)
.
{\displaystyle {\frac {1-\cos(\theta )}{\theta ^{2}}}={\frac {\sin(\theta )}{\theta }}\times {\frac {\sin(\theta )}{\theta }}\times {\frac {1}{1+\cos(\theta )}}.}
Os limites destas três quantidades são 1, 1 e 1/2, então o limite resultante é 1/2.
Prova de composições de funções trigonométricas e trigonométricas inversas [ editar | editar código-fonte ] Todas estas funções seguem da identidade trigonométrica pitagórica. Podemos provar por exemplo a função
sin
[
arctan
(
x
)
]
=
x
1
+
x
2
{\displaystyle \sin[\arctan(x)]={\frac {x}{\sqrt {1+x^{2}}}}}
Prova:
Partindo de
sin
2
(
θ
)
+
cos
2
(
θ
)
=
1
{\displaystyle \sin ^{2}(\theta )+\cos ^{2}(\theta )=1}
dividimos esta equação por
cos
2
(
θ
)
{\displaystyle \cos ^{2}(\theta )}
cos
2
(
θ
)
=
1
tan
2
(
θ
)
+
1
.
{\displaystyle \cos ^{2}(\theta )={\frac {1}{\tan ^{2}(\theta )+1}}.}
Então usando a substituição
θ
=
arctan
(
x
)
{\displaystyle \theta =\arctan(x)}
1
−
sin
2
[
arctan
(
x
)
]
=
1
tan
2
[
arctan
(
x
)
]
+
1
.
{\displaystyle 1-\sin ^{2}[\arctan(x)]={\frac {1}{\tan ^{2}[\arctan(x)]+1}}.}
Então usando a identidade
tan
[
arctan
(
x
)
]
≡
x
{\displaystyle \tan[\arctan(x)]\equiv x}
sin
[
arctan
(
x
)
]
=
x
x
2
+
1
.
{\displaystyle \sin[\arctan(x)]={\frac {x}{\sqrt {x^{2}+1}}}.}
Referências 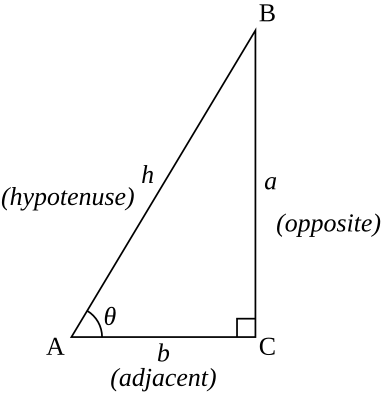



















































































































































![{\displaystyle \sin[\arctan(x)]={\frac {x}{\sqrt {1+x^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d3ed8cedb4c73b01b65314a15152647c9000086)




![{\displaystyle 1-\sin ^{2}[\arctan(x)]={\frac {1}{\tan ^{2}[\arctan(x)]+1}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/805997773901d54b0eb3789d0e5fe7e94667a7eb)
![{\displaystyle \tan[\arctan(x)]\equiv x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49ce3dc146ff12eb2efb89a4388afcb984b7da8e)
![{\displaystyle \sin[\arctan(x)]={\frac {x}{\sqrt {x^{2}+1}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc86f3356ccd6842ce81433191035143892230ec)