Saltar para o conteúdo

Transição vítrea

Origem: Wikipédia, a enciclopédia livre.

A transição vítrea é a transição reversível em materiais amorfos (ou em regiões amorfas de materiais semi-cristalinos) entre um estado duro e relativamente rígido e um estado mole e "borrachoso" (como um líquido de ultra-alta viscosidade).[1] Um sólido amorfo que exibe uma transição vítrea é dito vítreo. O processo de super-resfriar um líquido viscoso até o estado vítreo é chamado de vitrificação, do latim vitreum, "vidro" via francês vitrifier, "vitrificar".

Apesar de uma mudança profunda nas propriedades físicas de um material quando da sua transição vítrea, esse processo não é uma mudança de fase (como fusão ou solidificação), mas sim um fenômeno que se estende ao longo de uma faixa de temperatura definido por uma série de convenções.[2][3] Tais convenções incluem uma constante de taxa de resfriamento (20 K/min)[1] e um limiar de viscosidade de 1012 Pa·s, entre outros parâmetros. Aquecendo-se ou resfriando-se um material no intervalo de temperatura no qual ocorre a transição vítrea, esse material também apresenta uma suave variação no coeficiente de expansão térmica e no calor específico, efeito que dependerá do histórico do material (variações de temperatura e/ou pressão ou aplicações de forças às quais o material foi submetido ao longo do tempo). Entretanto, a questão de quando uma transição de fase constitui uma transição vítrea continua sendo estudada.[2][3][4]

A temperatura de transição vítrea, Tg (do inglês glass transition temperature), é um valor representativo de aproximadamente metade do intervalo de transição vítrea, e é sempre menor que a temperatura de fusão, Tm (do inglês melting temperature) ou Tf , do material no estado cristalino, se esse existir.

Introdução

[editar | editar código-fonte]

A transição vítrea de um líquido para um estado "semi-sólido" ocorre com diminuição de temperatura ou pressão.[5] A transição compreende um aumento na viscosidade (η) do material em 17[carece de fontes?] ordens de magnitude sem uma pronunciada mudança estrutural. A consequência desse aumento é um material vítreo que apresenta propriedades mecâncias de um sólido na escala de tempo de observação prática. Esta transição se dá em contraste com a que ocorre quando do congelamento ou cristalização, que é uma transição de fase de primeira ordem, segundo a classificação de Ehrenfest e envolve descontinuidades nas propriedades dinâmicas e termodinâmicas, como volume, energia e viscosidade. Para vários materiais que sofrem solidificação, um resfriamento rápido evita essa transição de fase e, em vez disso, resulta em uma transição vítrea em uma temperatura mais baixa. Outros materiais, como diversos polímeros, não apresentam um estado cristalino bem definido e facilmente formam fase amorfa vítrea, mesmo com resfriamento bastante lento ou compressão. A tendência de um material apresentar-se no estado vítreo quando resfriado é chamada "glass forming ability", ou "capacidade de formação de fase vítrea", numa tradução livre do inglês. Essa capacidade depende da composição do material, e pode-se ter uma previsão dela por meio da Teoria da Rigidez.[6]

Abaixo dessa faixa de temperatura, a estrutura amorfa vítrea não apresenta relaxação diretamente relacionada à taxa de resfriamento à qual o material foi submetido. O coeficiente de expansão térmica para o estado vítreo é mais ou menos equivalente ao de um sólido cristalino. Quando são usadas taxas de resfriamento lentas, necessita-se de maior tempo para que ocorra relaxação estrutural (rearranjo intermolecular para um estado de menor energia), o que resulta em uma maior densidade do produto final. De maneira semelhante, com o recozimento, que permite uma relaxação estrutural mais lenta, a estrutura vítrea se aproxima, ao longo do tempo, de um equilíbrio correspondente a um líquido super-resfriado à mesma temperatura. A Tg é dada pela intersecção entre as curvas de resfriamento (volume x temperatura) para os estados vítreo e líquido super-resfriado.[7][8][9][10][11]

A configuração do material vítreo nesse intervalo de temperatura modifica-se lentamente até que se atinja a estrutura de equilíbrio. O princípio de minimização da energia livre de Gibbs provê a força termodinâmica necessária para a modificação. Deve-se notar que, a temperaturas superiores à Tg, a estrutura que corresponde àquela de equilíbrio a qualquer temperatura é atingida rapidamente. Em contraste a isso, em temperaturas consideravelmente baixas, a configuração do material vítreo permanece praticamente estável a longos períodos de tempo.

Portanto, a transição vítrea não é uma transição entre estados de equilíbrio termodinâmico. Acredita-se largamente que o verdadeiro estado de equilíbrio termodinâmico é sempre cristalino e que os materiais vítreos existem em um estado cineticamente travado, de modo que sua entropia, sua densidade e outras propriedades dependam do seu histórico térmico. Entretanto, a transição vítrea é primariamente um fenômeno dinâmico. Tempo e temperatura são grandezas intercambiáveis (até certo ponto) quando trata-se de vidros, fato frequentemente expresso pelo Princípio da Superposição Tempo-Temperatura. Ao resfriar-se um líquido, "graus de liberdade internos sucessivamente 'saem' do equilíbrio". No entanto, há uma grande discussão acerca da existência de uma transição de fase de segunda ordem no limite hipotético de tempos de relaxação infinitamente longos.[12][13][14][15]

Temperatura de Transição Vítrea

[editar | editar código-fonte]
Determinação da Tg por técnica de DSC (calorimetria diferencial de varredura), mostrando a capacidade térmica em função da temperatura. A Tg é o ponto de intersecção das retas cinzas. (u.a. = unidades arbitrárias)

O gráfico à direita mostra a determinação da temperatura de transição vítrea, Tg, pela técnica de DSC (calorimetria diferencial de varredura), apresentando a capacidade térmica de um material vítreo em função da temperatura. Antes do início da transição vítrea, a capacidade térmica do material varia linearmente; ao longo da faixa de temperatura em que ocorre a transição, varia de modo a formar uma curva; e após a transição, volta a variar linermente, mas com coeficiente angular diferente. Neste contexto, a Tg é a temperatura que corresponde ao ponto de intersecção dos dois segmentos de reta. Outro método para determinação da temperatura de transição vítrea, bastante parecido na sua interpretação, é a dilatometria. Da mesma forma como a capacidade térmica varia, o coeficiente de expansão térmica também apresenta esse mesmo comportamento, de modo que os gráficos são semelhantes, e a Tg é também a intersecção das retas dadas por uma regressão linear.[16]

Diferentes definições operacionais de Tg são usadas, e várias delas são aceitas como normas científicas. No entanto, todas essas definições são arbitrárias, e cada uma leva a resultados numéricos diferentes: na melhor das hipóteses, valores de Tg para uma mesma substância variam por poucos Kelvin. Outra definição refere-se à viscosidade (η), fixando a Tg como aquela em que o efeito viscoso atinge o valor de 1013 poise (ou 1012 Pa·s). Conforme evidenciado experimentalmente, esse valor é próximo à temperatura de recozimento de vários vidros.[17]

Ao contrário da viscosidade η, a expansão térmica, a capacidade térmica, o módulo de cisalhamento e várias outras propriedades de vidros apresentam uma variação brusca quando a Tg é alcançada. Qualquer uma dessas propriedades pode ser usada para definir a Tg, desde que a taxa de aquecimento ou resfriamento seja especificada para que os resultados sejam reprodutíveis.

A definição de Tg mais frequentemente empregada usa a liberação de energia no aquecimento por DSC, aplicando inicialmente uma taxa de resfriamento de −10 °C/min e em seguida aquecendo à taxa de 10 °C/min. Outra definição de Tg é dada por dilatometria ou análise termomecânica, observando a expansão térmica do material. Neste caso, a taxa de aquecimento aplicada varia de 3 a 5 °C/min. Abaixo são apresentados valores característicos de Tg para alguns materiais.

Polímeros

[editar | editar código-fonte]
Polímero Tg (°C)
Polietileno de baixa densidade (LDPE) −125[18]
Borracha (pneu) −70[19]
Poli(fluoreto de vinilideno) (PVDF) −35[20]
Polipropileno (PP) (atático) −20[21]
Pol(fluoreto de vinila) (PVF) −20[20]
Polipropileno (PP) (isotático) 0[21]
Poli-3-hidroxibutirato (PHB) 15[21]
Poli(acetato de vinila) (PVAc) 30[21]
Poli(clorotrifluoroetileno) (PCTFE) 45[20]
Poli(tereftalato de etileno) (PET) 70[21]
Poli(cloreto de vinila) (PVC) 80[21]
Poli(álcool vinílico) (PVA) 85[21]
Poliestireno (PS) 95[21]
Poli(metacrilato de metila) (PMMA) (atático) 105[21]
Poli(acrilonitrila-butadieno-estireno) (ABS) 105[22]
Politetrafluoroetileno (PTFE) 115[23]
Policarbonato (PC) 145[21]
Polissulfona 185
Polinorborneno 215[21]

O Nylon-6 apresenta Tg de 47 °C,[24] e o Nylon-6,6, de aproximadamente 70 °C,[25] enquanto o PE pode apresentar Tg variando de −130 a −80 °C de acordo com o método de síntese e o processamento[26] Deve-se ter em mente que esses valores são os mais comuns, visto que a Tg depende da taxa de resfriamento, da distribuição de massa molecular e da presença de aditivos. Além disso, para polímeros semi-cristalinos (como PE e PP, que apresentam entre 60 e 80% de cristalinidade a temperatura ambiente), esses valores de Tg se referem apenas à parte amorfa do polímero.

Silicatos e outros materiais vítreos covalentes

[editar | editar código-fonte]
Material Tg (°C)
Calcogeneto GeSbTe 150[27]
Calcogeneto AsGeSeTe 245
ZBLAN (vidro de fluoretos) 235
Dióxido de telúrio 280
Fluoroaluminato 400
Vidro sodo-cálcico 520–600
Quartzo fundido ~1200[28]

O Paradoxo de Kauzmann

[editar | editar código-fonte]

À medida que o líquido é super-resfriado, a diferença de entropia entre as fases sólida e líquida diminui. Por extrapolação da capacidade térmica de um líquido super-resfriado abaixo da sua Tg, é possível calcular a temperatura na qual a diferença entre as entropias é zero. Tal temperatura é chamada a temperatura de Kauzmann de um material.

Se um líquido pudesse ser resfirado a temperaturas menores que sua temperatura de Kauzmann, e mesmo assim apresentasse uma entropia menor que a da fase cristalina, as consequências disso seriam paradoxais. Este "paradoxo de Kauzmann" tem sido tema de vários debates e publicações desde que foi apresentado pela primeira vez por Walter Kauzmann em 1948.[29]

Uma solução proposta é dizer que deve ocorrer uma transição de fase antes de a entropia do líquido diminuir. Neste cenário, a temperatura de transição é conhecida como "temperatura de transição vítrea calorimétrica ideal", T0c. Nessa visão, a transição vítrea não é meramente um efeito cinético, i.e., o resultado do resfriamento rápido de um fundido, mas sim constitui uma base termodinâmica para a formação do estado vítreo. Esse comportamento da temperatura de transição vítrea é dado pela seguinte expressão:

à medida que

Ou seja, a Tg tende a T0c assim como a variação de temperatura num intervalo infinitesimal de tempo tende a zero.

Há pelo menos outras três possíveis soluções para o paradoxo de Kauzmann. Uma delas define que a capacidade térmica de um líquido super-resfriado a temperatura próxima à de Kauzmann diminui suavemente para um valor menor. Propõe-se também que uma transição de fase de primeira ordem para outro estágio do estado líquido ocorre antes da temperatura de Kauzmann com a capacidade térmica desse estágio sendo menor do que a obtida por extrapolação da temperatura de Kauzmann (mais alta). Finalmente, o próprio Kauzmann resolveu seu paradoxo de entropia postulando que líquidos super-resfriados devem cristalizar antes que a temperatura de Kauzmann seja atingida, caso contrário, forma-se o sólido amorfo.

A transição vítrea para alguns materiais

[editar | editar código-fonte]

Sílica, SiO2

[editar | editar código-fonte]
Estrutura amorfa da sílica, SiO2, em duas dimensões.

Sílica (o composto químico SiO2) possui várias formas cristalinas diferentes além do quartzo. Quase todas são formadas pela unidade tetraedral SiO4 unidas por vértices compartilhados (oxigênio) em diferentes arranjos cristalinos. O comprimento das ligações Si―O varia para diferentes cristais. Por exemplo, no quartzo-α, o comprimento da ligação é 161 pm, enquanto na tridimita-α ele pode variar de 154 a 71 pm. O ângulo da ligação Si―O―Si varia de 140° na tridimita-α para 144° no quartzo-α e para 180° na tridimita-β. Quaisquer divergências em relação a esse padrão constituem variações ou diferenças microestruturais que representam uma aproximação para os sólidos amorfos ou sólidos vítreos. A Tg, para os silicatos, está relacionada à energia requerida para quebrar e/ou formar novas ligações covalentes numa rede amorfa. A Tg é claramente influenciada pelas características químicas do vidro. Por exemplo, a adição de elementos como boro, sódio, potássio ou cálcio a um vidro de sílica, que tenham valência menor que 4, ajuda na quebra de ligações da estrutura, reduzindo a Tg. Alternativamente, fósforo, que tem valência 5, ajuda a fortalecer a rede, portanto aumentando a Tg.[30] A Tg é diretamente proporcional à força de ligação, i.e., depende de parâmetros termodinâmicos de quase-equilíbrio das ligações, como a entalpia Hd e a entropia Sd dos configurons, excitações elementares resultantes de ligações rompidas em materiais amorfos, como vê-se na seguinte equação (M. I. Ojovan, 2008):

onde R é constante universal dos gases ideais e fc é o limiar de percolação. Para "fundidos fortes" (líquidos para os quais log(η) é linear em relação a Tg / T), como SiO2, o limiar de percolação na equação é a "densidade crítica universal de Scher-Zallen no espaço tridimensional", ou seja, fc = 0.15, e, para "líquidos frágeis" (log(η) é não-linear em relação a Tg / T), o limiar de percolação é uma propriedade dependente do material, sendo fc << 1.[31] A entalpia Hd e a entropiaSd dos configurons podem ser determinadas a partir informações experimentais obtidas da viscosidade.[32]

Polímeros

[editar | editar código-fonte]
Cadeias amorfas de polímero em imagem obtida por microscopia de força atômica (AFM).

Para os polímeros, a temperatura de transição vítrea, Tg, é frequentemente expressa como a temperatura em que a energia livre de Gibbs é tal que a energia de ativação para o movimento cooperativo das cadeias poliméricas é atingida[carece de fontes?], fazendo com que o material passe de sólido rígido para borrachoso. Isso permite que as cadeias deslizem umas sobre as outras quando uma força é aplicada. A partir dessa definição, pode-se perceber que a introdução de grupos químicos relativamente rígidos (como anéis aromáticos) interfere no fluxo do polímero, consequentemente aumentando a Tg.[33] A rigidez dos termoplásticos diminui devido a esse efeito. Quando a Tg é atingida, a rigidez permanece a mesma por um curto período de tempo, i.e., em ou próximo a E2, até que a temperatura exceda Tm, e o polímero derreta. Esta região é chamada de platô ou estado borrachoso.

Quando se passa um tecido a ferro, as fibras atingem temperaturas superiores à Tg, passando pela transição vítrea-borrachosa.
Rigidez de um polímero amorfo em funcão da temperatura, apresentando o platô borrachoso.

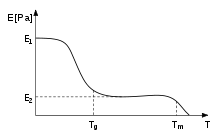
Ao passar-se a ferro um tecido, este é aquecido temperaturas superiores à Tg, de modo que suas fibras, que são cadeias poliméricas, tornam-se móveis no estado borrachoso. O peso do ferro sobre o tecido e o sentido no qual o tecido é passado impõem uma orientação às cadeias. A Tg pode ser significativamente reduzida pela adição de plastificantes ao polímero no processamento. Moléculas menores de plastificante incorporam-se entre as cadeias, fazendo aumentar o espaço e o volume livre, e permitindo que elas tenham mobilidade a temperaturas mais baixas. O popular "cheiro de carro novo" se deve à volatilização dessas moléculas, mais comumente ftalatos, empregados para modificar os polímeros usados nas peças plásticas do interior do veículo (como o painel) com o objetivo de evitar rachaduras em dias frios devido à contração do material. A adição de grupos não-reativos ao polímero também pode dar esse mesmo efeito, reduzindo a Tg. Se um polímero cujas propriedades são desejadas tem uma Tg muito alta, ele pode ser combinado a outro polímero, dando origem a um copolímero com uma Tg mais baixa, permitindo a aplicação. Deve-se notar que alguns plásticos são usados a altas temperaturas, como em motores de automóveis, e outros, a baixas temperaturas, como as embalagens de polietileno para produtos congelados.[21] Para materiais viscoelásticos, a ocorrência de um comportamento quase-líquido depende das propriedades do material (i.e., da contribuição do estado líquido nas propriedades do material no estado borrachoso) e varia com a taxa de carga aplicada, i.e., o quão rápido a força é aplicada. O brinquedo "Silly Putty" (conhecido no Brasil como "geleca"), que consiste em uma massa de silicone colorida, comporta-se de uma maneira diferente de acordo com a taxa, o tempo e a direção de aplicação de uma força: comprimindo-a lentamente, ela escoa como um líquido de alta viscosidade; martelando-a, ela se quebra, como um material vítreo rígido.

Ao serem resfriados, os elastômeros passam também por uma transição líquido-vítrea (de um líquido para um sólido amorfo vítreo), que também pode ser chamada de "transição vítreo-borrachosa". O desastre do ônibus espacial Challenger foi causado pelo fato de anéis de vedação de borracha da estrutura estarem sendo empregados em temperatura bastante inferior à sua Tg em uma manhã de frio incomum na Flórida, de modo que não se flexionaram da maneira adequada para vedar seções entre os dois solid rocket boosters, que são os foguetes laterais auxiliares do lançamento.

Mecânica de vitrificação

[editar | editar código-fonte]

Movimentos moleculares na matéria condensada podem ser representados por uma série de Fourier cuja interpretação física consiste em uma superposição de ondas longitudinais e transversais do deslocamento atômico com variação de direção e de comprimento de onda. Para sistemas monoatômicos, essas ondas são chamadas de "flutuações de densidade", e para sistemas poliatômicos, devem ser incluídas também "flutuações composicionais"[34]

Portanto, o movimento térmico em líquidos pode ser decomposto em vibrações longitudinais elementares (ou fônons acústicos) enquanto que as vibrações transversais (ondas cisalhantes) eram originalmente descritas somente em sólidos elásticos exibindo o estado cristalino altamente ordenado da matéria. Em outras palavras, líquidos simples não podem resistir à aplicação de uma força na forma de tensão cisalhante, e irão ceder mecanicamente através de deformação plástica macroscópica (fluxo viscoso). Além disso, o fato de que um sólido deforma localmente enquanto preserva sua rigidez é aceito como a distinção entre os dois estados, mecanicamente.[35][36]

As inadequações dessa conclusão, no entanto, foram apontadas por Frenkel na sua revisão da Teoria Cinética dos Sólidos e Teoria da Elasticidade dos Líquidos. Essa revisão segue diretamente desde as características contínuas da transição estrutural do estado líquido para o sólido quando essa transição não é acompanhada de cristalização — portanto um líquido viscoso super-resfriado. Desse modo, se vê uma correlação íntima entre fônons transversais (ondas cisalhantes) e o início da rigidez sobre a vitrificação, como descreveu Bartenev na sua descrição mecânica do processo de vitrificação.[37][38]

As velocidades dos fônons acústicos longitudinais na matéria condensada são diretamente responsáveis pela condutividade térmica que nivela diferenças de temperatura entre elementos de volumes comprimidos e expandidos termicamente. Kittel propôs que o comportamento dos vidros e demais materiais vítreos fosse interpretado em termos de um livre caminho médio aproximadamente constante para os fônons da rede, e que o valor desse livre caminho médio é da ordem de magnitude da escala de desordem na estrutura molecular de um líquido ou sólido. O livre caminho médio ou o comprimento de relaxação de um fônon térmico de uma série de vidros formadores foi plotado em função da temperatura de transição vítrea, indicando que há uma relação linear entre os dois. Isso sugeriu um novo critério para a formação de vidros baseado no valor do livre caminho médio.[39]

Frequentemente se tem sugerido que a condução de calor em sólidos dielétricos ocorre através das vibrações elásticas da rede, sendo limitada pelo espalhamento elástico por fônons longitudinais por defeitos da rede (como vacâncias espaçadas aleatoriamente).[40] Essas previsões foram confirmadas por experimentos em vidros e vitrocerâmicas comerciais, nos quais o livre caminho médio era aparentemente limitado por "espalhamento do limite interno" para comprimentos entre 10 e 100 µm.[41][42] A relação entre essas ondas transversais e o mecanismo de vitrificação foi descrita por vários autores, os quais propuseram que o início das correlações entre vários fônons resulta em uma ordenação orientada ou "congelada" das tensões cisalhantes locais em fundidos que darão origem a materiais vítreos, então gerando a transição vítrea.[43]

Estrutura Eletrônica

[editar | editar código-fonte]

A influência dos fônons e a interação deles com a estrutura eletrônica é um assunto que foi apropriadamente introduzido na discussão da resistência elétrica de metais líquidos. A Teoria de Lindemann da Fusão é referenciada, e sugere-se que a queda na condutividade quando da transição do estado cristalino para o líquido se deve ao maior espalhamento dos elétrons condutores resultante do aumento da amplitude das vibrações atômicas. Tal teoria de localização tem sido aplicada para o transporte em vidros metálicos (metais amorfos), nos quais o livre caminho médio dos elétrons é bastante pequeno, da ordem do espaço interatômico.[44][45]

A formação de um sólido não-cristalino de uma liga ouro-silício pelo método de splat quenching (resfriamento ultra-rápido) a partir do fundido levou a outras considerações acerca da influência da estrutura eletrônica na capacidade de formação da estrutura vítrea, baseando-se nas propriedades das ligações metálicas.[46][47][48][49][50]

Outro trabalho indica que a mobilidade de elétrons localizados é aumentada pela presença de vários modos de fônons dinâmicos. Um contraponto a esse modelo é de que se ligações químicas são importantes, o modelo do elétron livre próximo não devia ser aplicável. No entanto, se o modelo inclui o acúmulo de uma distribuição de carca entre todos pares de átomos como uma ligação química (como no silício, quando uma banda é preenchida com elétrons), então essa teoria deveria se aplicar aos sólidos.[51]

Então, se a condutividade elétrica é baixa, o livre caminho médio dos elétrons é bastante curto. Eles somente serão sensíveis a ordem de curto alcance em um vidro (materiais vítreos inorgânicos, em geral) se não houver chance de espalharem-se entre átomos separados por longas distâncias. Como a ordem de curto alcance é semelhante para vidros e critais, as energias eletrônicas são similares para esses dois estados. Em ligas de baixa resistividade e livre caminho médio maior, a desordem é maior para os elétrons, de modo que isso aumentaria sua energia e desestabilizaria o vidro em relação à cristalização. Portanto, a tendência de vitrificação de certas ligas deve-se ao fato de o livre caminho médio ser bastante curto, e consequentemente apenas a ordem de curto alcance é importante para a energia dos elétrons.

Também argumentou-se que a formação de estruturas vítreas em sistemas metálicos está relacionada à "suavidade" do potencial de interação entre átomos distintos. Alguns autores, enfatizando as fortes similaridades entre a estrura local do "vidro metálico" formado e a estrutura cristalina correspondente, sugerem que as ligações químicas ajudam a estabilizar a estrutura amorfa.[52][53]

Outros autores sugerem que a estrutura eletrônica exerce sua influência na formação do vidro através das propriedades direcionais das ligações. A não-cristalinidade é portanto favorecida por elementos que apresentam polimorfismo e têm ligações químicas anisotrópicas. A cristalização torna-se mais desfavorável à medida que a anisotropia das ligações é aumentada de materiais metálicos isotrópicos para metálicos anisotrópicos e então para materiais covalentes, portanto sugerindo uma relação entre a família química (na tabela periódica) e a habilidade de formar estruturas vítreas em sólidos elementares.[54]

Referências

  1. ↑ a b ISO 11357-2: Plastics – Differential scanning calorimetry (DSC) – Part 2: Determination of glass transition temperature (1999).
  2. ↑ a b Debenedetti, P. G.; Stillinger (2001). «Supercooled liquids and the glass transition». Nature. 410 (6825): 259–267. Bibcode:2001Natur.410..259D. PMID 11258381. doi:10.1038/35065704 
  3. ↑ a b Angell, C. A.; Ngai, K. L.; McKenna, G. B.; McMillan, P. F.; Martin, S. W. (2000). «Relaxation in glassforming liquids and amorphous solids». App. Phys. Rev. 88 (6): 3113–3157. Bibcode:2000JAP....88.3113A. doi:10.1063/1.1286035 
  4. ↑ Ojovan, M. I. (2004). «Glass formation in amorphous SiO2 as a percolation phase transition in a system of network defects». Journal of Experimental and Theoretical Physics Letters. 79 (12). 632 páginas. Bibcode:2004JETPL..79..632O. doi:10.1134/1.1790021 
  5. ↑ Hansen, J.-P.; McDonald, I. R.; (2007). Theory of Simple Liquids. [S.l.]: Elsevier. pp. 250–254. ISBN 0123705355 
  6. ↑ Phillips, J.C. (1979). «Topology of covalent non-crystalline solids I: Short-range order in chalcogenide alloys». Journal of Non-Crystalline Solids. 34 (2): 153. Bibcode:1979JNCS...34..153P. doi:10.1016/0022-3093(79)90033-4 
  7. ↑ Moynihan, C. et al. in The Glass Transition and the Nature of the Glassy State, Eds. M. Goldstein and R. Simha, Ann. N.Y. Acad. Sci., Vol. 279 (1976) ISBN 0890720533
  8. ↑ Angell, C. A. (1988). «Perspective on the glass transition». Journal of Physics and Chemistry of Solids. 49 (8). 863 páginas. Bibcode:1988JPCS...49..863A. doi:10.1016/0022-3697(88)90002-9 
  9. ↑ Ediger, M. D.; Angell, C. A.; Nagel, Sidney R. (1996). «Supercooled Liquids and Glasses». The Journal of Physical Chemistry. 100 (31). 13200 páginas. doi:10.1021/jp953538d 
  10. ↑ Angell, C. A. (1995). «Formation of Glasses from Liquids and Biopolymers». Science. 267 (5206): 1924–35. Bibcode:1995Sci...267.1924A. PMID 17770101. doi:10.1126/science.267.5206.1924 
  11. ↑ Stillinger, F. H. (1995). «A Topographic View of Supercooled Liquids and Glass Formation». Science. 267 (5206): 1935–9. Bibcode:1995Sci...267.1935S. PMID 17770102. doi:10.1126/science.267.5206.1935 
  12. ↑ Zarzycki, J. (1991). Glasses and the Vitreous State. [S.l.]: Cambridge University Press. ISBN 0521355826 
  13. ↑ Nemilov, S. V., (1994). Thermodynamic and Kinetic Aspects of the Vitreous State. [S.l.]: CRC Press. ISBN 0849337828 
  14. ↑ J. H. Gibbs (1960). J. D. MacKenzie, ed. Modern Aspects of the Vitreous State. [S.l.]: Butterworth. OCLC 1690554 
  15. ↑ Ojovan, Michael I; Lee, William (Bill) E (2010). «Connectivity and glass transition in disordered oxide systems». Journal of Non-Crystalline Solids. 356 (44–49). 2534 páginas. Bibcode:2010JNCS..356.2534O. doi:10.1016/j.jnoncrysol.2010.05.012 
  16. ↑ Tg measurement of glasses. Glassproperties.com. Retrieved on 2012-06-29.
  17. ↑ glass-transition temperature Arquivado em 22 de dezembro de 2014, no Wayback Machine., IUPAC Compendium of Chemical Terminology, 66, 583 (1984)
  18. ↑ Polyethylene, Canada: D&M Plastics, 2007, A Tg do PE depende do processamento, então os valores dependerão da amostra. 
  19. ↑ Galimberti, Maurizio; Caprio, Michela; Fino, Luigi (21 de dezembro de 2001). «Tyre comprising a cycloolefin polymer, tread band and elasomeric composition used therein». country-code =EU, patent-number WO03053721 
  20. ↑ a b c Christopher C. Ibeh (2011). THERMOPLASTIC MATERIALS Properties, Manufacturing Methods, and Applications. [S.l.]: CRC Press. pp. 491–497. ISBN 978-1-4200-9383-4 
  21. ↑ a b c d e f g h i j k l Wilkes, C. E. (2005). PVC Handbook. [S.l.]: Hanser Verlag. ISBN 1-56990-379-4 
  22. ↑ ABS Arquivado em 13 de junho de 2010, no Wayback Machine. Retrieved 7 May 2010
  23. ↑ John W. Nicholson (2011). The Chemistry of Polymers 4, Revised ed. [S.l.]: Royal Society of Chemistry. 50 páginas. ISBN 1849733910. Consultado em 10 de setembro de 2013. ISBN=9781849733915 
  24. ↑ nylon-6 information and properties. Polymerprocessing.com (2001-04-15). Retrieved on 2012-06-29.
  25. ↑ Supplementary Materials for Artificial Muscles from Fishing Line and Sewing Thread. Science 343, 868, Fig. S12. 21 February 2014. DOI: 10.1126/science.1246906.
  26. ↑ PCL | Applications and End Uses | Polythene. Polyesterconverters.com. Retrieved on 2012-06-29.
  27. ↑ EPCOS 2007: Glass Transition and Crystallization in Phase Change Materials Arquivado em 26 de julho de 2011, no Wayback Machine. . Retrieved on 2012-06-29.
  28. ↑ Bucaro, J. A.; H. D. (1 de dezembro de 1974). «High‐temperature Brillouin scattering in fused quartz». Journal of Applied Physics. 45 (12): 5324-5329. ISSN 0021-8979. doi:10.1063/1.1663238 
  29. ↑ Kauzmann, Walter (1948). «The Nature of the Glassy State and the Behavior of Liquids at Low Temperatures». Chemical Reviews. 43 (2). 219 páginas. doi:10.1021/cr60135a002 
  30. ↑ Ojovan M.I. (2008). «Configurons: thermodynamic parameters and symmetry changes at glass transition» (PDF). Entropy. 10 (3): 334–364. Bibcode:2008Entrp..10..334O. doi:10.3390/e10030334 
  31. ↑ Ojovan, M.I. (2008). «Configurons: thermodynamic parameters and symmetry changes at glass transition» (PDF). Entropy. 10 (3): 334–364. Bibcode:2008Entrp..10..334O. doi:10.3390/e10030334 
  32. ↑ Ojovan, Michael I; Travis, Karl P; Hand, Russell J (2007). «Thermodynamic parameters of bonds in glassy materials from viscosity–temperature relationships». Journal of Physics: Condensed Matter. 19 (41). 415107 páginas. Bibcode:2007JPCM...19O5107O. doi:10.1088/0953-8984/19/41/415107 
  33. ↑ Cowie, J. M. G. and Arrighi, V., Polymers: Chemistry and Physics of Modern Materials, 3rd Edn. (CRC Press, 2007) ISBN 0748740732
  34. ↑ Slater, J.C., Introduction to Chemical Physics (3rd Ed., Martindell Press, 2007) ISBN 1178626598
  35. ↑ Born, Max (2008). «On the stability of crystal lattices. I». Mathematical Proceedings of the Cambridge Philosophical Society. 36 (2). 160 páginas. Bibcode:1940PCPS...36..160B. doi:10.1017/S0305004100017138 
  36. ↑ Born, Max (1939). «Thermodynamics of Crystals and Melting». The Journal of Chemical Physics. 7 (8). 591 páginas. Bibcode:1939JChPh...7..591B. doi:10.1063/1.1750497 
  37. ↑ Frenkel, J. (1946). Kinetic Theory of Liquids. [S.l.]: Clarendon Press, Oxford 
  38. ↑ Bartenev, G. M., Structure and Mechanical Properties of Inorganic Glasses (Wolters – Noordhoof, 1970) ISBN 9001054501
  39. ↑ C. L. Reynolds Jr. (1979). «Correlation between the low temperature phonon mean free path and glass transition temperature in amorphous solids». J. Non-Cryst. Sol. 30 (3): 371. Bibcode:1979JNCS...30..371R. doi:10.1016/0022-3093(79)90174-1 
  40. ↑ Rosenburg, H. M., Low Temperature Solid State Physics (Clarendon Press, Oxford, 1963)
  41. ↑ Kittel, C. (1946). «Ultrasonic Propagation in Liquids». J. Chem. Phys. 14 (10): 614. Bibcode:1946JChPh..14..614K. doi:10.1063/1.1724073 
  42. ↑ Kittel, C. (1949). «Interpretation of the Thermal Conductivity of Glasses». Phys. Rev. 75 (6): 972. Bibcode:1949PhRv...75..972K. doi:10.1103/PhysRev.75.972 
  43. ↑ Chen, Shao-Ping; Egami, T.; Vitek, V. (1985). «Orientational ordering of local shear stresses in liquids: A phase transition?». Journal of Non-Crystalline Solids. 75. 449 páginas. Bibcode:1985JNCS...75..449C. doi:10.1016/0022-3093(85)90256-X 
  44. ↑ N. F. Mott (1934). «The Resistance of Liquid Metals». Proceedings of the Royal Society A. 146 (857): 465. Bibcode:1934RSPSA.146..465M. doi:10.1098/rspa.1934.0166 
  45. ↑ C. Lindemann (1911). Phys. Zeitschr. 11: 609 
  46. ↑ Klement, W.; Willens, R. H.; Duwez, POL (1960). «Non-crystalline Structure in Solidified Gold–Silicon Alloys». Nature. 187 (4740). 869 páginas. Bibcode:1960Natur.187..869K. doi:10.1038/187869b0 
  47. ↑ Duwez, Pol; Willens, R. H.; Klement, W. (1960). «Continuous Series of Metastable Solid Solutions in Silver-Copper Alloys». Journal of Applied Physics. 31 (6). 1136 páginas. Bibcode:1960JAP....31.1136D. doi:10.1063/1.1735777 
  48. ↑ Duwez, Pol; Willens, R. H.; Klement, W. (1960). «Metastable Electron Compound in Ag-Ge Alloys». Journal of Applied Physics. 31 (6). 1137 páginas. Bibcode:1960JAP....31.1137D. doi:10.1063/1.1735778 
  49. ↑ Chaudhari, P; Turnbull, D (1978). «Structure and properties of metallic glasses». Science. 199 (4324): 11–21. Bibcode:1978Sci...199...11C. PMID 17841932. doi:10.1126/science.199.4324.11 
  50. ↑ J. S. Chen (1980). «Glassy metals». Reports on Progress in Physics. 43 (4): 353. Bibcode:1980RPPh...43..353C. doi:10.1088/0034-4885/43/4/001 
  51. ↑ M. Jonson, S. M. Girvin (1979). «Electron-Phonon Dynamics and Transport Anomalies in Random Metal Alloys». Phys. Rev. Lett. 43 (19): 1447. Bibcode:1979PhRvL..43.1447J. doi:10.1103/PhysRevLett.43.1447 
  52. ↑ D. Turnbull (1974). «Amorphous Solid Formation and Interstitial Solution Behavior in Metallic Alloy System». J. Phys. C. 35 (C4): C4–1. doi:10.1051/jphyscol:1974401 
  53. ↑ H. S. Chen, B. K. Park (1973). «Role of chemical bonding in metallic glasses». Acta Met. 21 (4): 395. doi:10.1016/0001-6160(73)90196-X 
  54. ↑ R. Wang, D. Merz (1977). «Polymorphic bonding and thermal stability of elemental noncrystalline solids». Physica Status Solidi (a). 39 (2): 697. Bibcode:1977PSSAR..39..697W. doi:10.1002/pssa.2210390240 
Obtida de "https://pt.wikipedia.org/w/index.php?title=Transição_vítrea&oldid=68741132"