Usuário(a):RBiazzi/Teoria de cabos

Visão simplificada da teoria de cabos em uma fibra neuronal

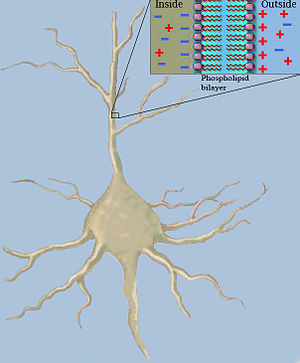
A teoria de cabos usa modelos matemáticos para calcular a corrente elétrica (e a voltagem que a acompanha) ao longo de neuritos passivos, particularmente os dendritos que recebem sinais decorrentes das sinapses de outros neurônios, em diferentes regiões e instantes de tempo. As estimativas são feitas modelando dendritos e axônios como cilindros compostos de segmentos com capacitâncias $c_{m}$ e resistências $r_{m}$ combinados em paralelo. A inclusão da capacitância na modelagem de uma fibra neuronal é decorrência da presença de forças eletrostáticas que agem através da fina Bicapa lipídica. A resistência em série ao longo da fibra $r_{l}$, por sua vez, deve-se à significativa resistência do ao movimento da carga elétrica.

Capacitância da fibra

História

A teoria de cabos na neurociência computacional tem raízes que remontam à década de 1850, quando o professor William Thomson (mais tarde conhecido como Lorde Kelvin) começou a desenvolver modelos matemáticos a respeito do decaimento de sinais em cabos telegráficos submarinos. Os modelos se assemelhavam às equações diferenciais parciais usadas por Fourier para descrever a condução de calor em um fio.

A década de 1870 viu as primeiras tentativas de Hermann para modelar potenciais elétricos neuronais, ainda focado em analogias com as teorias sobre condução de calor. No entanto, foi Hoorweg quem primeiro propôs as analogias com os cabos submarinos de Kelvin em 1898 e, em seguida, Hermann e Cremer desenvolveram independentemente a teoria de cabos para fibras neuronais no início do século XX. Outras teorias matemáticas de condução de fibra nervosa com base na teoria de cabos foram desenvolvidas por Cole e Hodgkin (1920-1930), Offner et al. (1940) e Rushton (1951).

A evidência experimental da importância da teoria de cabos na modelagem do comportamento dos axônios começou a surgir na década de 1930 a partir do trabalho feito por Cole, Curtis, Hodgkin, Sir Bernard Katz, Rushton, Tasaki e outros. Dois artigos importantes dessa época são os de Davis e Lorente de Nó (1947) e Hodgkin e Rushton (1946).

A década de 1950 viu melhorias nas técnicas de medição da atividade elétrica de neurônios individuais. Assim, a teoria de cabos tornou-se importante para analisar dados coletados de gravações de microeletrodos intracelulares e para analisar as propriedades elétricas de dendritos neuronais. Cientistas como Coombs, Eccles, Fatt, Frank, Fuortes e outros agora confiavam fortemente na teoria de cabos para obter informações funcionais de neurônios e orientá-los no projeto de novos experimentos.

Mais tarde, a teoria de cabos com suas derivadas matemáticas permitiu que modelos de neurônios cada vez mais sofisticados fossem explorados por pesquisadores como Jack, Rall, Redman, Rinzel, Idan Segev, Tuckwell, Bell e Iannella. Mais recentemente, a teoria de cabos foi aplicada para modelar a atividade elétrica em neurônios agrupados na substância branca do cérebro.

Derivando a equação do cabo

Observe que existem várias convenções de $r_{m}$. Aqui, $r_{m}$ e $c_{m}$, como introduzidos acima, são medidos por unidade de comprimento de membrana (metro). Assim, $r_{m}$ é medido em ohm ·metros (Ω·m) ecm em farads por metro (F/m). Isso está em contraste com $R_{m}$ (em Ω·m ² ) e $C_{m}$ (em F/m ² ), que representam a resistência específica e a capacitância, respectivamente, de uma unidade de área de membrana (em m ² ). Assim, se o raio, $a$, do axônio for conhecido, então sua circunferência é $2\pi a$, e seu $r_{m}$, e seus valores $c_{m}$ podem ser calculados como:

${\begin{aligned}r_{m}&=R_{m}/2\pi a\\c_{m}&=C_{m}\cdot 2\pi a\end{aligned}}$

Essas relações fazem sentido intuitivamente, porque quanto maior a circunferência do axônio, maior a área para a carga escapar através de sua membrana e, portanto, menor a resistência da membrana (dividindo $R_{m}$ por $2\pi a$); e mais membrana disponível para armazenar carga (multiplicando $C_{m}$ por $2\pi a$). A resistência elétrica específica, $\rho _{l}$, do axoplasma permite calcular a resistência intracelular longitudinal por unidade de comprimento, $r_{l}$, (em Ω·m ⁻¹ ) pela equação:

$r_{l}={\frac {\rho _{l}}{\pi a^{2}}}$

Quanto maior a área da seção transversal do axônio, $\pi a^{2}$, maior o número de caminhos para a carga fluir através de seu axoplasma e menor a resistência axoplasmática.

Vários caminhos importantes para estender a teoria clássica do cabo viram recentemente a introdução de estruturas endógenas para analisar os efeitos da polarização da proteína dentro dos dendritos e diferentes distribuições de entrada sináptica sobre a superfície dendrítica de um neurônio.

Para entender melhor como a equação do cabo é derivada, primeiro simplifique ainda mais o neurônio teórico e imagine que ele tenha uma membrana perfeitamente selada ($r_{m}=\inf$) sem perda de corrente para o exterior e sem capacitância ($c_{m}=0$). Uma corrente injetada na fibra na posição $x=0$ se moveria ao longo do interior da fibra inalterado. Afastando-se do ponto de injeção e usando a lei de Ohm ($V=RI$), podemos calcular a variação de tensão como:

$\Delta V=-i_{l}r_{l}\Delta x$

onde o negativo é porque a corrente flui a favor do gradiente de potencial.

Deixando $\Delta x$ ir em direção a zero e tendo incrementos infinitamente pequenos de $x$, pode-se escrever como:

${\frac {\partial V}{\partial x}}=-i_{l}r_{l}$

ou

${\frac {1}{r_{l}}}{\frac {\partial V}{\partial x}}=-i_{l}$

Trazer $r_{m}$ de volta à cena é como fazer furos em uma mangueira de jardim. Quanto mais furos, mais rápido a água escapará da mangueira e menos água percorrerá todo o caminho desde o início até o fim da mangueira. Da mesma forma, em um axônio, parte da corrente que viaja longitudinalmente pelo axoplasma escapará pela membrana.

Se $i_{m}$ é a corrente que escapa através da membrana por unidade de comprimento, m, então a corrente total que escapa ao longo de $y$ unidades deve ser $y\cdot i_{m}$. Assim, a mudança de corrente no axoplasma, $\Delta i_{l}$, na distância, $\Delta x$, da posição $x=0$ pode ser escrita como:

$\Delta i_{l}=-i_{m}\Delta x$

ou, usando incrementos infinitesimalmente pequenos contínuos:

${\frac {\partial i_{l}}{\partial x}}=-i_{m}$

$i_{m}$ pode ser expressa com outra fórmula, incluindo a capacitância. A capacitância causará um fluxo de carga (uma corrente) em direção à membrana no lado do citoplasma. Esta corrente é geralmente referida como corrente de deslocamento (aqui denotada $i_{c}$ . ) O fluxo só ocorrerá enquanto a capacidade de armazenamento da membrana não for atingida. $i_{c}$ pode então ser expressa como:

$i_{c}=c_{m}{\frac {\partial V}{\partial t}}$

onde $c_{m}$ é a capacitância da membrana e ${\partial V}/{\partial t}$ é a variação da tensão ao longo do tempo. A corrente que passa pela membrana ( $i_{r}$ ) pode ser expressa como:

$i_{r}={\frac {V}{r_{m}}}$

e porque $i_{m}=i_{r}+i_{c}$ a seguinte equação para $i_{m}$ pode ser derivada se nenhuma corrente adicional for adicionada de um eletrodo:

${\frac {\partial i_{l}}{\partial x}}=-i_{m}=-\left({\frac {V}{r_{m}}}+c_{m}{\frac {\partial V}{\partial t}}\right)$

onde ${\partial i_{l}}/{\partial x}$ representa a variação por unidade de comprimento da corrente longitudinal.

A combinação das equações e fornece uma primeira versão de uma equação de cabo:

${\frac {1}{r_{l}}}{\frac {\partial ^{2}V}{\partial x^{2}}}=c_{m}{\frac {\partial V}{\partial t}}+{\frac {V}{r_{m}}}$

que é uma equação diferencial parcial de segunda ordem (PDE).

Por um simples rearranjo da equação (veja mais adiante) é possível fazer com que dois termos importantes apareçam, a saber, a constante de comprimento (algumas vezes chamada de constante de espaço) denotada $\lambda$ e a constante de tempo denotada $\tau$ . As seções a seguir se concentram nesses termos.

Constante de comprimento

A constante de comprimento, $\lambda$ (lambda), é um parâmetro que indica o quanto uma corrente estacionária influenciará a tensão ao longo do cabo. Quanto maior o valor de $\lambda$, mais longe a carga fluirá. A constante de comprimento pode ser expressa como:

$\lambda ={\sqrt {\frac {r_{m}}{r_{l}}}}$

Quanto maior a resistência da membrana, r _m, maior o valor de $\lambda$, e mais corrente permanecerá dentro do axoplasma para viajar longitudinalmente pelo axônio. Quanto maior a resistência axoplasmática, $r_{l}$, menor o valor de $\lambda$, mais difícil será para a corrente viajar através do axoplasma, e mais curta a corrente será capaz de viajar. É possível resolver a equação e chegar à seguinte equação (válida em condições estacionárias, ou seja, quando o tempo se aproxima do infinito):

$V_{x}=V_{0}e^{-{\frac {x}{\lambda }}}$

Onde $V_{0}$ é a despolarização em $x=0$ (ponto de injeção de corrente), $e$ é a constante exponencial (valor aproximado 2,71828) e $V_{x}$ é a tensão a uma dada distância $x$ de $x=0$. Quando $x=\lambda$ então

${\frac {x}{\lambda }}=1$

e

$V_{x}=V_{0}e^{-1}$

o que significa que quando medimos $V$ à distância $\lambda$ de $x=0$ Nós temos

$V_{\lambda }={\frac {V_{0}}{e}}=0.368V_{0}$

Por isso $V_{\lambda }$ é sempre 36,8% de $V_{0}$.

Tempo constante

Os neurocientistas estão frequentemente interessados em saber a velocidade com que o potencial de membrana, $V_{m}$, de um axônio muda em resposta a mudanças na corrente injetada no axoplasma. A constante de tempo, $\tau$, é um índice que fornece informações sobre esse valor. $\tau$ pode ser calculado como:

$\tau =r_{m}c_{m}$

Quanto maior a capacitância da membrana, $c_{m}$, mais corrente é necessária para carregar e descarregar um pedaço de membrana e mais tempo esse processo levará. Quanto maior a resistência da membrana $r_{m}$, mais difícil é para uma corrente induzir uma mudança no potencial de membrana. Então quanto mais alto $\tau$ mais lento o impulso nervoso pode viajar. Isso significa que o potencial de membrana (tensão através da membrana) fica mais para trás das injeções de corrente. Os tempos de resposta variam de 1 a 2 milissegundos em neurônios que estão processando informações que precisam de alta precisão temporal até 100 milissegundos ou mais. Um tempo de resposta típico é de cerca de 20 milissegundos.

Forma genérica e estrutura matemática

Se multiplicarmos a equação por $r_{m}$ em ambos os lados do sinal de igual, obtemos:

${\frac {r_{m}}{r_{l}}}{\frac {\partial ^{2}V}{\partial x^{2}}}=c_{m}r_{m}{\frac {\partial V}{\partial t}}+V$

e reconhecer $\lambda ^{2}={r_{m}}/{r_{l}}$ do lado esquerdo e $\tau =c_{m}r_{m}$ do lado direito. A equação do cabo agora pode ser escrita em sua forma talvez mais conhecida:

$\lambda ^{2}{\frac {\partial ^{2}V}{\partial x^{2}}}=\tau {\frac {\partial V}{\partial t}}+V$

Esta é uma equação de calor 1D ou equação de difusão para a qual muitos métodos de solução, como as funções de Green e os métodos de Fourier, foram desenvolvidos.

É também um caso especial degenerado da equação do telégrafo, onde a indutância $L$ desaparece e a velocidade de propagação do sinal $1/{\sqrt {LC}}$ é infinito.

Ver também

• Axônio
• Modelo de neurônio biológico
• Dendrito
• Modelo de Hodgkin-Huxley
• Potencial elétrico de membrana
• Equação Nernst–Planck
• Patch clamp

Referências

• Poznanski, Roman R. (2013). Mathematical Neuroscience. San Diego [California]: Academic Press 
• Tuckwell, Henry C. (1988). Introduction to theoretical neurobiology. Cambridge [Cambridgeshire]: Cambridge University Press. ISBN 978-0521350969 
• de Nó, Rafael Lorente (1947). A study of nerve physiology. Col: Studies from the Rockefeller Institute for Medical Research. Reprints, v. 2. [S.l.]: Rockefeller Institute for Medical Research. pp. Part I, 131:1–496; Part II, 132:1–548. ISBN 9780598674722. OCLC 6217290 
• Lazarevich, Ivan A.; Kazantsev, Victor B. (2013). «Dendritic signal transition induced by intracellular charge in inhomogeneties». Phys. Rev. E. 88 (6): 062718. Bibcode:2013PhRvE..88f2718L. PMID 24483497. arXiv:1308.0821. doi:10.1103/PhysRevE.88.062718 
• Douglas, PK; Douglas, David B. (2019). «Reconsidering Spatial Priors In EEG Source Estimation : Does White Matter Contribute to EEG Rhythms?». 7th International Winter Conference on Brain-Computer Interface (BCI), Gangwon, Korea (South). 88: 1-12. ISBN 978-1-5386-8116-9. arXiv:2111.08939. doi:10.1109/IWW-BCI.2019.8737307 

Notas

Passive here refers to the membrane resistance being voltage-independent. However recent experiments (Stuart and Sakmann 1994) with dendritic membranes shows that many of these are equipped with voltage gated ion channels thus making the resistance of the membrane voltage dependent. Consequently there has been a need to update the classical cable theory to accommodate for the fact that most dendritic membranes are not passive.

Classical cable theory assumes that the fiber has a constant radius along the distance being modeled.

Classical cable theory assumes that the inputs (usually injections with a micro device) are currents which can be summed linearly. This linearity does not hold for changes in synaptic membrane conductance.}}