Círculo de quintas

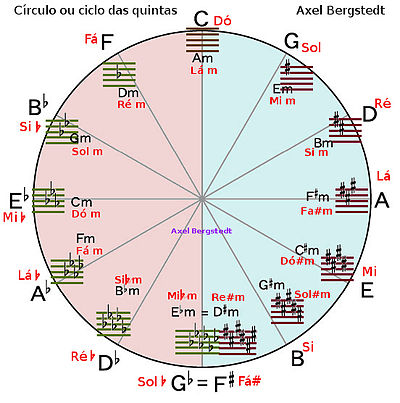
Círculo de quintas é um espaço geométrico circular que descreve as relações entre as doze notas da escala cromática de temperamento igual.[1] Ao tocarmos uma nota qualquer da escala e irmos ascendendo sucessivamente por intervalos de quinta perfeita usando igual temperamento, chegamos sempre a mesma nota 1 oitava acima, depois de passarmos por todas as outras da escala cromática. Como o espaço é circular, é também possível seguir a sucessão em sentido contrário, subtraindo intervalos de quinta perfeita. Nesse caso, obtemos uma sucessão de intervalos de quarta. Por essa razão, o círculo de quintas é também conhecido pelo nome de círculo de quartas.
Ciclo de quintas[editar | editar código-fonte]
Se usarmos quintas perfeitas naturais, ou Quintas Justas Puras, o espaço deixa de ser circular. Esta quinta justa pura corresponde exatamente à relação de 3:2 entre as frequências fundamentais de dois sons. Por exemplo, se tomarmos o Lá3 440 Hz como referência, a quinta justa pura acima corresponderá ao Mi4 660 Hz. . Desta forma, ascendendo sucessivamente doze intervalos de quinta perfeita, não chegamos exatamente a uma nota igual. Isto tem que ver com o fato de que 3n=2m, nunca se verifica para n e m inteiros. Ou seja, usando intervalos de quinta que correspondem a um fator 3n ou 3n/2k entre frequências, nunca obteremos oitavas perfeitas, as quais correspondem a um fator 2m).[2]
O ciclo de quintas naturais resulta nos intervalos, expressos em frações (razão) e em cents, que se apresentam em seguida:
| razão | nota | cents |
|---|---|---|
| 8192/6561 | (Fá♭) | 384,36 |
| 4096/2187 | (Dó♭) | 1086,315 |
| 1024/729 | (Sol♭) | 588,27 |
| 256/243 | (Ré♭) | 90,225 |
| 128/81 | (Lá♭) | 792,18 |
| 32/27 | (Mi♭) | 294,135 |
| 16/9 | (Si♭) | 996 |
| 4/3 | (Fá) | 498 |
| 1/1 | (Dó) | 0 |
| 3/2 | (Sol) | 701,9 |
| 9/8 | (Ré) | 203,9 |
| 27/16 | (Lá) | 905,9 |
| 81/64 | (Mi) | 407,8 |
| 243/128 | (Si) | 1109,8 |
| 729/512 | (Fá♯) | 611,7 |
| 2187/2048 | (Dó♯) | 113,68 |
| 6561/4096 | (Sol♯) | 815,64 |
| 19683/16384 | (Ré♯) | 317,595 |
| 59049/32768 | (Lá♯) | 905,9 |
| 177147/131072 | (Mi♯) | 521,505 |
| 531441/262144 | (Si♯) | 1223,46 |
Como se pode ver, em vez de um dó uma oitava acima, obtemos um Si♯ que dista 1223,46 cents de dó, em vez de distar 1200 cents. É a essa diferença de -23,46 cent que se chama de coma pitagórica. A história dos sistemas de temperamentos roda em volta de vários esquemas de alteração dos intervalos de quinta de modo que o ciclo de quintas resulte num intervalo de oitava, tentando alcançar o maior número de intervalos o mais perto dos naturais que for possível.
Na escala pitagórica, usavam-se exatamente esses intervalos, resultando num ciclo de 11 quintas perfeitas: Mi♭ - Si♭ - Fá - Dó - Sol - Ré - Lá - Mi - Si - Fá♯ - Dó♯ - Sol♯. A 12.ª quinta usada era (Ré♯ - Mi♭), para fechar o círculo. Essa quinta correspondia a um intervalo de 678,485 cent, em vez de 701,9 cent, absorvendo toda a coma ditónica, ficando assim dissonante. Por essa razão se chamava a "quinta do lobo", por ficar "uivando". Note que na escala pitagórica, as notas enarmónicas distam da coma pitagórica. Os sustenidos são mais agudos do que os bemóis correspondentes. Por exemplo, Fá♯ é uma nota mais aguda do que Sol♭. Na escala de temperamento igual, as quintas perfeitas não são naturais, sendo todas encurtadas de 701,9 cent, para 700 cent, ficando ligeiramente desafinadas em relação ao terceiro harmónico da nota fundamental.[3]
Uso[editar | editar código-fonte]
A memorização do ciclo de quintas, e consequentemente as notas ou graus que estão perto uns dos outros, nos permite harmonizar, improvisar e analisar melhor os trechos de uma música. Por exemplo, uma cadência típica na harmonia tradicional seria: Dó maior - Ré menor 7 - Sol 7 - Dó maior: repare como as notas ou graus dos acordes seguem o ciclo de quintas no sentido anti-horário. O ciclo de quinta nos mostra quais notas são mais próximas ou que soam mais consonantes com a nota tocada. Um acorde de dó (C) maior se parece muito com um acorde de Fá ou de Sol, sendo assim em alguns casos podemos substituir um pelo outro.
Tons vizinhos e tons afastados[editar | editar código-fonte]
Ao lado direito de um tom (tônica) encontra-se a dominante (5º grau da escala), no exemplo de C é o G. Ao lado esquerdo se encontra a subdominante (grau IV). Em baixo do tom se encontra o tom relativo (grau VI a partir do tom original que é chamado de sobredominante ou relativa da tônica). Esses três acordes são os vizinhos diretos do tom ou da tônica, que são os mais importantes na harmonização de músicas. (Se o tom ou a tônica é menor, vale o mesmo: os três tons vizinhos são a dominante na direita e a subdominante na esquerda e o tom relativo em cima, então no caso de Em seriam Bm, Am e G. Porém, na prática da harmonização a dominante menor é muitas vezes substituída pelo mesmo acorde em maior, no exemplo anterior então seria B em lugar de Bm.) Os dois tons relativos em cima ou em baixo da dominante e subdominante são chamados de tons vizinhos indiretos, eles são como parentes de segundo grau. Eles representam o grau II (supertônica ou relativa da subdominante) e grau III (mediante ou relativa da dominante).
Achamos, então, os seis primeiros graus da escala ao redor de um tom, e eles são os tons vizinhos (como uma família ou um grupo de amigos). Para harmonizar uma melodia se usam principalmente esses acordes. Em músicas simples como cânticos, hinos e músicas populares eles representam mais de 90% dos acordes. Acontece, porém, que uma música faz uma modulação e passa a ter temporariamente uma nova tônica. Na maioria das vezes a dominante vira a nova tônica. No trecho respectivo se usam os tons vizinhos da nova tônica.[4]
Tom próximo[editar | editar código-fonte]
Acontece que um tom menor é substituído pelo mesmo tom em maior, como no exemplo em cima B em lugar de Bm. Também o contrário acontece. Os dois modos maior e menor tem uma grande afinidade, a maioria dos tons são iguais. Por isso eles se chamam "tons próximos", embora que não estejam muito avizinhados no círculo das quintas. B é então um tom próximo de Bm e vice-versa.[5]
Referências
- ↑ MED, Bohumil. Teoria da música. Musimed, Brasília DF:1996.
- ↑ BENNETT, Roy. Elementos básicos da música. Jorge Zahar, São Paulo:1998.
- ↑ BENNETT, Roy. Como Ler uma partitura. Jorge Zahar, São Paulo:1990.
- ↑ Med, Bohumil (1996). Teoria da música 4ª ed. Brasília: Musimed. p. 162ss. ISBN 85-85886-02-1
- ↑ Med, Bohumil (1996). Teoria da música 4ª ed. Brasília: Musimed. p. 158ss. ISBN 85-85886-02-1
