Raiz quadrada de dois

A hipotenusa de um triângulo retângulo cujos catetos medem 1 tem comprimento raiz quadrada de dois.

A raiz quadrada de dois, denotada ${\sqrt {2}}$, é o único número real positivo cujo quadrado (ou seja, o resultado de sua multiplicação por si próprio) é dois:

${\sqrt {2}}\times {\sqrt {2}}=2$.

A raiz quadrada de dois é um número irracional, ou seja, não é possível encontrar dois números inteiros $a$ e $b$ tais que ${\frac {a}{b}}={\sqrt {2}}.$

Acredita-se que ${\sqrt {2}}$ tenha sido o primeiro número irracional reconhecido como tal. Esta importante descoberta é atribuída a Hipaso de Metaponto, da escola de Pitágoras. De acordo com uma lenda, a demonstração teria custado a vida de seu descobridor, uma vez que contrariava as ideias predominantes entre os pitagóricos de que tudo era número (inteiro).

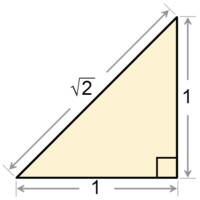
Um triângulo retângulo cujos catetos medem 1 tem hipotenusa com comprimento ${\sqrt {2}}$.

Notação

A raiz quadrada de dois pode ser escrita como:

• ${\sqrt {2}}$, lê-se "raiz quadrada de dois" ou "raiz de dois".
• $2^{\frac {1}{2}}$ ou $2^{1/2}$, lê-se "dois elevado a um meio" ou "dois a um meio".

Aproximação decimal da raiz quadrada de 2

Por ser um número irracional, ${\sqrt {2}}$ não pode ser expressa como um número finito de casas decimais, uma aproximação com 65 dígitos decimais é:

1,41421356237309504880168872420969807856967187537694807317667973799... (sequência A002193 na OEIS).

Uma aproximação fraccionária para a raiz quadrada de 2 é 10/7 que, ao quadrado, fica 100/49, bem próximo de 2.

Sequência aproximante de raiz quadrada de 2

Pode-se facilmente construir uma seqüência de números racionais se aproximando (convergindo) para ${\sqrt {2}}$:

$\left\{{\begin{array}{l}x_{0}=1\\x_{n+1}={\frac {x_{n}}{2}}+{\frac {1}{x_{n}}}\end{array}}\right.$

Esta recursão produz a seqüência:

$1;~~{\frac {3}{2}};~~{\frac {17}{12}};~~{\frac {577}{408}};~~{\frac {665857}{470832}};~~{\frac {886731088897}{627013566048}}$

Ou, aproximadamente:

$1;~~1,5;~~1.416666667;~~1.414215686;~~1.414213562;~~1.414213562$

Observe que o método estabiliza a nona casa decimal após apenas cinco passos.

Inexistência de um número racional cujo quadrado seja 2

O matemático britânico Godfrey Harold Hardy em seu livro Em defesa de um matemático afirma que a demonstração da irracionalidade da raiz quadrada de dois é um dos teoremas de "primeira classe". E que "conserva a beleza e o frescor que tinha ao ser descoberto" há mais de dois mil anos.

A demonstração é simples e recorre ao método da prova por contradição. Ou seja, supomos que exista um número racional igual a raiz de 2, ou seja, que existem números inteiros positivos $a$ e $b$ tais que:

${\frac {a}{b}}={\sqrt {2}}$

ou, equivalentemente:

$\left({\frac {a}{b}}\right)^{2}=2$

Podemos supor que $a$ e $b$ não são ambos números pares, pois se fossem, poderíamos simplificar a fração até obter um dos termos da fração ímpar.

Agora, escrevemos:

$\left({\frac {a}{b}}\right)^{2}={\frac {a^{2}}{b^{2}}}=2$

Então:

$a^{2}=2b^{2}$

Concluímos então que $a^{2}$ deve ser um número par, pois é dobro de $b^{2}$. $a$ deve ser par também, pois o quadrado de um número ímpar é ímpar.

Temos então que $a$ é um número par e, portanto, é o dobro de algum número inteiro, digamos $c$:

$a=2c$

$(2c)^{2}=2b^{2}$

$4c^{2}=2b^{2}$

$2c^{2}=b^{2}$

Pelos motivos alegados anteriormente, $b$ deve ser um número par.

Concluímos, finalmente, que se a raiz quadrada de 2 fosse um número racional, então este número seria uma fração que não tem forma irredutível, já que tanto o numerador quanto o denominador da fração são pares. Isto é um absurdo e, portanto, não existe um racional cujo quadrado seja igual a 2, como queríamos demonstrar.

Ligações externas

• «Cinco milhões de casas decimais da raiz quadrada de 2» (em inglês)