Grafo de Holt
| Grafo de Holt | |
|---|---|
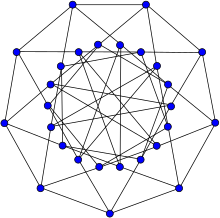 No grafo de Holt, todos os vértices são equilvalentes, e todas as arestas são equivalentes, mas as arestas não são necessáriamente equivalentes as suas inversas.
| |
| Nomeado em honra a | Derek F. Holt |
| vértices | 27 |
| arestas | 54 |
| Raio | 3 |
| Diâmetro | 3 |
| Cintura | 5 |
| Automorfismos | 54 |
| Número cromático | 3 |
| Índice cromático | 5 |
| Propriedades | Vértice-transitivo Aresta-transitivo Meio-transitivo grafo de Cayley Hamiltoniano Euleriano |
No campo da matemática da teoria dos grafos o grafo de Holt ou grafo de Doyle é o menor grafo meio-transitivo, ou seja, o menor exemplo de grafo vértice-transitivo e aresta-transitivo que não é também simétrico.[1][2] Esses grafos não são comuns.[3] É nomeado em honra a Peter G. Doyle e Derek F. Holt, que descobriram o mesmo grafo de forma independente em 1976[4] e 1981[5] respectivamente.
O grafo de Holt tem um diâmetro de 3, raio 3, cintura 5, número cromático 3, índice cromático 5 e é hamiltoniano com 98472 ciclos distintos hamiltonianos.[6] é também um grafo 4-vértice-conectado e 4-aresta-conectado.
Ele tem um grupo de automorfismo da ordem de 54 automorfismos.[6] Este é um grupo menor que um grafo simétrico com o mesmo número de vértices e arestas teria. O desenho do grafo à direita destaca isto, na medida em que carece de simetria reflexiva.
O polinômio característico do grafo de Holt é:
Galeria[editar | editar código-fonte]
-
O número cromático do grafo de Holt é 3.
-
O índice cromático do grafo de Holt é 5.
-
O grafo de Holt é Hamiltoniano.
Referências
- ↑ Doyle, P. "A 27-Vertex Graph That Is Vertex-Transitive and Edge-Transitive But Not L-Transitive." October 1998. [1]
- ↑ ALSPACH, Brian; MARUŠIČ, Dragan; NOWITZ, Lewis (1994). «Constructing Graphs which are ½-Transitive». Journal of the Australian Mathematical Society (Series A). 56 (3). pp. 391–402. doi:10.1017/S1446788700035564.
- ↑ Jonathan L. Gross, Jay Yellen, Handbook of Graph Theory, CRC Press, 2004, ISBN 1584880902, p. 491.
- ↑ Doyle, P. G. (1976), On Transitive Graphs, Senior Thesis, Harvard College. Como citado pela MathWorld.
- ↑ HOLT, Derek F. (1981). «A graph which is edge transitive but not arc transitive». Journal of Graph Theory. 5 (2). pp. 201–204. doi:10.1002/jgt.3190050210.
- ↑ a b Weisstein, Eric W. «Doyle Graph» (em inglês). MathWorld




