Estrela (polígono)

Grupo dos Polígonos Regulares
Exemplo: Um pentagrama regular (estrela pentagonal: {5/2})
Símbolo Schläfli 2<2q<p MDC(p,q)=1	{p/q}
Vértices e Arestas	5
Diagrama de Coxeter–Dynkin
Symmetry group	Diedral (D_p)
Poliedro dual	Autodual
Ângulo interno (graus)	$(1-{\frac {2q}{p}})\times 180$

Estrelas são polígonos que não parecem ter sido ainda formalmente definidos. Pode-se dizer apenas que são polígonos que se parecem com estrelas. Somente estrelas regulares foram estudadas com alguma profundidade.

Estrelas regulares[editar | editar código-fonte]

Na geometria, uma estrela poligonal regular é um polígono equilateral, equiangular que se autointersecta. Ele é criado se conectando os vértices não adjacentes de um polígono simples e regular de n lados, continuando o processo até que o vértice de onde se partiu seja atingido novamente. Por exemplo, em um pentágono regular, uma estrela de cinco pontas pode ser obtida desenhando-se uma linha do primeiro ao terceiro vértice, do terceiro ao quinto, deste ao segundo, então ao quarto e retornando ao primeiro. Esse processo envolve n adições repetidas, sendo n o número de lados do polígono e o número x a ser somado n vezes é maior que 1 e menor que n-1, ou: 1 < x < n-1. A notação para tal polígono é {n/x} (ver símbolo Schläfli), que é igual a {n/n-x}. o polígono à direita é {5/2}.

Uma estrela poligonal regular também pode ser representada como uma sequência de estrelamentos de um polígono regular convexo central.

Estrelas poligonais regulares foram estudadas sistematicamente pela primeira vez por Thomas Bradwardine.

Exemplos[editar | editar código-fonte]

{5/2}	{7/2}	{7/3}	{8/3}	{9/2}	{9/4}

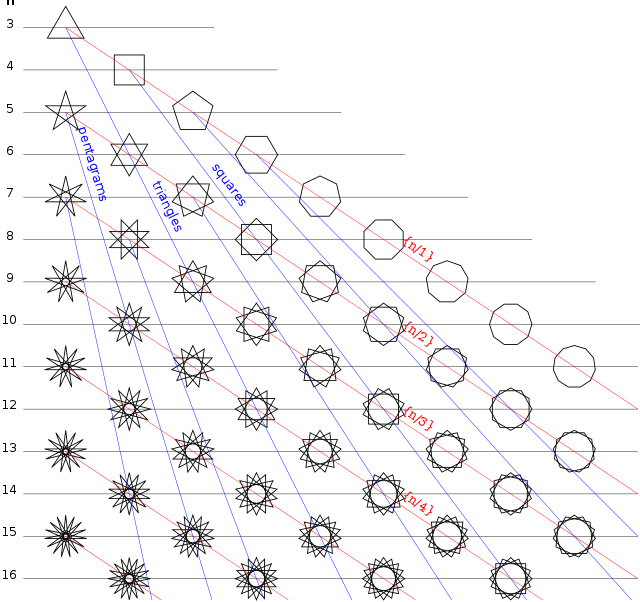
Figuras estelares[editar | editar código-fonte]

Se o número n de lados for divisível por m (i.e. sem deixar resto), a estrela obtida será um polígono regular de n/m lados. A nova figura é obtida rotacionando esses n/m-gons regulares um vértice para a esquerda no polígono original até o número de vértices rotacionados se iguale a n/m menos um, e então combinando essas duas figuras. Um caso extremo disso é onde n/m é 2, produzindo uma figura consistindo de n/2 segmentos de retas, chamado de polígono estelar degenerado.

Em outros casos onde n e m tem um fator em comum, o polígono estelar para um n menor é obtido e versões rotacionadas podem ser combinadas. Essas figuras são chamadas figuras estelares ou polígonos estelares impróprios ou polígonos compostos. A mesma notação {n/m} é frequentemente usada para eles, apesar de que autoridades como Grünbaum (1994) consideram (com alguma justificação) a forma k{n} mais correta, em que geralmente k=m.

Uma complicação maior ocorre quando se compõem dois ou mais polígonos estelares, como por exemplo dois pentagramas, diferindo por uma rotação de 36°, inscritos em um decágono. Isso é notado corretamente na forma k{n/m}, como 2{5/2}, em vez do mais frequente {10/4}.

Estrela Hexagonal[editar | editar código-fonte]

Uma estrela de seis pontas, como um hexágono, pode ser criada apenas com régua e compasso:

Faça um círculo de qualquer tamanho com o compasso.
Sem alterar o raio do compasso, coloque a ponta firme em qualquer ponto da circunferência e encontre um dos dois pontos onde um novo círculo interceptaria o primeiro.
Com a ponta fixa nesse último ponto, repita o procedimento para encontrar um terceiro ponto na circunferência, e depois um quarto quinto e sexto.
Com a régua, una pontos alternados para formar dois triângulos equiláteros sobrepostos.

Simetria[editar | editar código-fonte]

Polígonos estelares regulares e figuras estelares são consideradas grupos laterais diagramados dos subgrupos $x\mathbb {Z} _{n}$ do grupo finito $\mathbb {Z} _{n}$ .

O grupo de simetria de {n/k} é o grupo diedral D_n de ordem 2n, independente de k.

Polígonos estelares irregulares[editar | editar código-fonte]

Polígonos estelares irregulares cíclicos ocorrem como figuras de vértice verticiais para os poliedros uniformes, definidos pela sequência de arestas poligonais regulares a partir de cada vértice, permitindo múltiplas rotações e direções retrógradas. (See vertex figures at Lista de poliedros uniformes)

Na ilustração, a linha branca é uma figura de vértice hexagonal não-regular cíclica para o Grande icosidodecaedro retro-achatado. O comprimento das arestas são definidos pela distância entre vértices alternos nas faces do poliedro uniforme.

Interiores dos polígonos estelares[editar | editar código-fonte]

Polígonos estelares deixam uma ambiguidade quanto a interpretação de seus interiores. Esse diagrama mostra três interpretações distintas de um pentagrama.

1. A interpretação à esquerda possui 5 vértices de um pentágono regular conectados alternadamente, pulando vértices alternados. O interior é tudo imediatamente à esquerda (ou à direita) de cada aresta até a próxima intersecção. Isso faz com que a região pentagonal convexa central fique do "lado de fora" e em geral pode se determinar o lado de dentro por uma Regra par-ímpar binária contando quantas arestas são interceptadas por um ponto ao longo de um raio ao infinito.

2. A interpretação do meio também tem os 5 vértices de um pentágono regular conectados alternadamente. O interior pode ser tratado como:

a) o interior da linha perimetral de um decágono simples, como em 3.

b) having the central convex pentagonal region surrounded twice, because the starry perimeter winds round it twice.

3. A interpretação à direita cria novos vértices nas intersecções nas arestas (5 nesse caso) e define um novo decágono côncavo formado pela linha perimetral da primeira interpretação - deixa de ser um pentagrama, mas continua sendo um polígono estelar.

O que é a área dentro do pentagrama? Cada interpretação leva a uma resposta diferente.

Exemplos de interpretações de prismas estelares[editar | editar código-fonte]

Prisma heptagrâmico {7/2}:

Heptagramas com interior de 2 lados	Heptagramas com um perímetro interior simples

O prisma heptagrâmico acima mostra que diferentes interpretações podem criar aparências bem diferentes.

Construtores de modelos poliédricos, como Magnus Wenninger, geralmente representam as faces de polígonos estelares na forma côncava, sem arestas internas aparentes.

Polígonos estelares, arte e cultura[editar | editar código-fonte]

Polígonos estelares tem posição especial na arte e na cultura. Tais polígonos podem ou não ser regulares, mas são sempre altamente simétricos. Por exemplo:

O polígono estelar {5/2} conhecido como pentagrama, pentalpha ou pentângulo, considerado por alguns possuidor de significados ocultos.
O polígono estelar não-degenerado mais simples é formado por dois polígonos {6/2}(i.e., triângulos), o hexagrama (Estrela de Davi, Selo de Salomão).
A Estrela Mariana, o polígono estelar próprio para representações simbólicas de objetos celestiais para a Igreja Católica.
Os polígonos estelares {7/3} e {7/2}, conhecidos por heptagramas, também são possuidores de significados ocultos, particularmente na Cabala e na Wicca.
O polígono estelar complexo {8/2} (i.e. dois quadrados), é conhecido como Estrela de Lakshmi e figura no Hinduísmo;
O polígono estelar {8/3} (octagrama), e a estrela poligonal complexa de dois polígonos {16/6}, que são motivos geoméricos frequentes na arte e arquitetura islâmicas Mogol; a primeira é encontrada no brasão do Azerbaijão.
Uma estrela de onze pontas chamada hendecagrama, aparentemente foi usada no túmulo do Xá Nemat Ollah Vali.

Alguns símbolos baseados em estelas poligonais tem interlaçamentos, pequenas falhas, e/ou, no caso de uma figura estelar, cores diferentes.

Uma estrela {8/3} (octagrama) construído dentro de um octógono.

Referências

Cromwell, P.; Polyhedra, CUP, Hbk. 1997, ISBN 0-521-66432-2. Pbk. (1999), ISBN 0-521-66405-5.
Grünbaum, B. e G. C. Shephard; Tilings and Patterns, New York: W. H. Freeman & Co., (1987), ISBN 0-7167-1193-1.
Grünbaum, B.; Polyhedra with Hollow Faces, Proc of NATO-ASI Conference on Polytopes ... etc. (Toronto 1993), ed T. Bisztriczky et al, Kluwer Academic (1994) pp. 43–70.

Ver também[editar | editar código-fonte]