Lógica subjetiva
A lógica subjetiva é um tipo de lógica probabilística que explicitamente leva a incerteza e a própria crença em consideração. Em geral, a lógica subjetiva é adequada para modelar e analisar situações envolvendo incertezas e conhecimento incompleto.[1][2] Por exemplo, isto pode ser usado para modelar Redes Verdades e para análise de Redes Bayesianas.
Os argumentos na lógica subjetiva são opiniões subjetivas sobre proposições. Uma opinião binomial se aplica a uma única proposição, e pode ser representada como uma Distribuição beta. Uma opinião multinomial se aplica a uma coleção de proposições, e pode ser representada como uma Distribuição de Dirichlet. Através de correspondência entre opiniões e distribuições Beta/Dirichlet, a lógica subjetiva provê uma álgebra para essas funções. Opiniões são relacionadas com a funções de crença da Teoria de Dempster-Shafer.
Um aspecto fundamental da condição humana é que ninguém pode sempre determinar com certeza absoluta se uma proposições sobre o mundo é verdadeira ou falsa. Além disso, sempre que a verdade de uma proposição é expressa, isso é sempre feito por um indivíduo, e isto nunca pode ser considerado para representar uma crença geral e objetiva. Estas ideias filosóficas são diretamente refletidas no formalismo matemática da lógica subjetiva. Irracionalmente pode ser descrita em termos do que é conhecido como fuzzjetivo.
Opiniões subjetivas[editar | editar código-fonte]
Opiniões subjetivas expressam crenças subjetivas sobre a verdade das proposições com graus de incerteza, e podem indicar propriedades de crença subjetiva sempre que requisitado. Uma opinião é usualmente denotada como onde é o subjetivo, também conhecido como proprietário de crença e é a proposição para qual a opinião se aplica. Uma notação alternativa é . A proposição é assumida a pertencer de um quadro de discernimento (também chamado de estado de espaço) e.g. denotado como , mas o quadro é usualmente não incluído na notação de opinião. A proposição de um quadro é normalmente assumida exaustiva e mutualmente disjunta, e subjeções são assumidas para ter uma interpretação semântica comum das proposições. A subjeção, a proposição e seu quadro são atributos de uma opinião. Indicativos de propriedade de crença subjetiva é normalmente omitida sempre que irrelevante.
Opiniões binomiais[editar | editar código-fonte]
Seja ser uma proposição. Uma opinião binomial sobre a verdade de é o quádruplo ordenado onde:
| : crença | é a crença de que a proposição especificada seja verdadeira. |
| : descrença | é a crença de que a proposição especificada seja falsa. |
| : incerteza | é a quantidade de crenças não confirmadas. |
| : taxa base | é a probabilidade a priori na ausência de provas. |
Estes componentes satisfazem e . A característica de várias classes de opiniões são listadas abaixo.
| Uma opinião | onde | é equivalente à lógica binária VERDADEIRA, |
| onde | é equivalente à lógica binária FALSA, | |
| onde | ié equivalente à probabilidade tradicional. | |
| onde | expressa graus de incertezas, e | |
| onde | expressa incerteza total. |
A valor da probabilidade esperada de uma opinião é definida como .
Opiniões binomiais podem ser representadas em um triângulo equilátero como mostrado abaixo. Um ponto dentro do triângulo representa a tripla. O b,d,u-axes correm de um canto para o vértice oposto indicado pela Crença, Descrença ou Incerteza. Por exemplo, uma forte opinião positiva é representada por um pronto à frente do canto inferior direito do vértice de Crença. A taxa base, também conhecida como atomicidade relativa, é mostrada como um ponto vermelho juntamente com a linha base, e a probabilidade esperada , é formada por projetando a opinião na base, paralela à linha de projeção da taxa base. Opiniões sobre três proposições X, Y e Z são visualizadas no triângulo para a esquerda, e suas distribuições Beta equivalentes são visualizadas sobre o enredo para direita. Os valores numéricos e uma descrição verbal discreta de cada opinião é também apresentada.
Distribuições betas são normalmente denotadas como onde e são seus dois parâmetros. A opinião beta de uma distribuição de uma opinião binomial é a função
Opiniões multinomiais[editar | editar código-fonte]
Seja ser um quadro, isto é, um conjunto de de exaustivas e mútuas proposições disjuntas . Uma opinião multinomial sobre é a função composta , onde é um vetor de massa de crenças de proposições , é a massa incerta, e é um vetor de valores de taxa base sobre as proposições de . Estes componentes satisfazem e tão bem quanto .
Visualisando A visualização de opiniões multinomiais não é trivial. Opiniões trinomiais podem ser visualizadas como pontos dentro de uma pirâmide triangular, mas o aspecto 2D dos monitores de computador fariam isto impraticável. Opiniões com largas dimensões do que a trinomial não se prestam a visualização tradicional.
Distribuições de Dirichlet são normalmente denotadas como onde representa seus parâmetros. A distribuição de Dirichlet de uma opinião multinomial é a função onde o vetor de componentes é dado por
Operadores da Lógica Subjetiva[editar | editar código-fonte]
A maioria dos operadores na tabela abaixo são generalizações da lógica binária e dos operadores probabilísticos. Por exemplo adição pe uma simples generalização da adição de probabilidades. Muitos operadores são apenas significativos para combinar opiniões binomiais, mas alguns são aplicados à opiniões multinomiais.[3] A maioria dos operadores são binários, mas complemento é unário, dedução é ternário e abdução é quaternário. Veja as referências para detalhes matemáticos de cada operador.
| Operadores da lógica subjetiva | Notação do operador | Operador da lógica proposicional/binária |
|---|---|---|
| Adição [4] | União | |
| Subtração[4] | Diferença | |
| Multiplicação[5] | Conjunção/ AND | |
| Divisão[5] | Un-conjunção/ UN-AND | |
| Co-multiplicação[5] | Disjunção/ OR | |
| Co-divisão[5] | Un-disjunção/ UN-OR | |
| Complemento[1][2] | Negação | |
| Dedução[6][7] | Modus Ponens | |
| Abdução[7][8] | Modus Tollens | |
| Transitividade/ desconto[1][2][9] | n.a. | |
| Fusão cumulativa / consenso | n.a. | |
| Fusão aproximada[3][9] | n.a. |
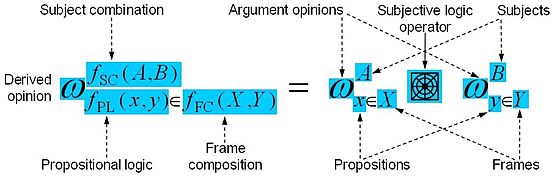
Além dos cálculos dos valores próprios das opiniões, operadores da lógica subjetiva também levam em conta os atributos, isto é, as subjeções, as proposições, bem como os quadros contendo as proposições. Em geral, os atributos das opiniões derivadas são funções dos atributos de argumentos, seguindo o princípio ilustrado abaixo. Por exemplo, a proposição derivada é tipicamente obtida usando o operador da lógica proposicional correspondente ao operador da lógica subjetiva.
As funções para derivar atributos dependem do operador. Alguns operadores assim como o cumulativo e o de fusão aproximada, apenas afetam o atributo subjetivo, não o proposicional que, em seguida, é igual à dos argumentos. Fusion por exemplo assume que dois argumentos subjetivos separados são fundidos em um só. Outros operadores, como a multiplicação, apenas afeta a proposição e seu quadro, não a subjeção que, em seguida, é igual ao do argumento. Multiplicação por exemplo assume que a proposição derivada é um conjunto de argumentos de proposições, e que o quadro derivado é composto como o produto cartesiano de dois quadros de argumento. O operador da transitividade é é o único operador onde tanto os atributos da subjeção e da proposição são afetados, mais especificamente por fazer a subjeção derivada igual a proposição e o quadro do segundo argumento de opinião.
É impraticável explicitar expressões combinações complexas subjetivas e expressões lógicas proposicionais como atributos de opiniões derivadas. Em vez disso, a verdadeira subjeção original e compacto termo da lógica proposicional pode ser usado.
Subjeções combinadas podem ser expressadas em uma compacta ou expandida forma, Por exemplo, o caminho verdadeiro transitivo de via para pode ser expressado como na forma compacta, ou como na forma expandida. A forma expandida é a mais genérica, e corresponde diretamente com o jeito que as expressões da lógica subjetiva são formadas com os operadores.
Propriedades[editar | editar código-fonte]
No caso dos argumentos de opinião serem equivalentes à lógica binária VERDADEIRO ou FALSO, o resultado de qualquer operador de lógica subjetiva é sempre igual ao do operador de lógica proposicional correspondente / binário. Do mesmo modo, quando as opiniões argumento são equivalentes às probabilidades tradicionais, o resultado de qualquer operador lógico subjectivo, isto é igual ao do operador probabilidade correspondente (quando ele existe).
No caso de argumentos de opinião conterem graus de incerteza, os operadores envolvendo multiplicação e divisão irão produzir opiniões derivadas que sempre possuem corretos valores esperados mas possivelmente com aproximações (variância) quando vistos como uma distribuição de probabilidade Beta/Dirichlet.[5] Todos os outros operadores produzir opiniões onde o valor esperado e a variância são sempre iguais aos valores analiticamente corretos.
Diferentes proposições compostas que tradicionalmente são equivalentes na lógica proposicional não necessariamente possuem opiniões iguais. Por exemplo em geral através da distributividade de conjuntos sobre disjunções, expressada como , segunda a proposição na lógica binária. Isso não é surpresa que os operadores de probabilidade correspondentes também são não-distributiva. No entanto, a multiplicação é distributiva sobre a adição, como expressa por . Leis de De Morgan também é satisfeita como algo do expresso da seguinte forma: .
Lógica subjectiva permite computação extremamente eficiente de modelos matematicamente complexos. Isto é possível através da aproximação das funções analiticamente corretas sempre que necessário. Enquanto isto é relativamente simples para análise multiplicando duas distribuições beta na forma de uma distribuição conjunta, nada mais complexo do que rapidamente se torna intratável. Ao combinar duas distribuições Beta com algum operador / conjuntivo, o resultado analítico nem sempre é uma distribuição Beta e pode envolver Séries Hipergeométricas .Em tais casos, a lógica sempre subjectiva aproxima o resultado como uma opinião que é equivalente a uma distribuição Beta.
Aplicações[editar | editar código-fonte]
Lógica subjetiva é aplicável quando a situação a ser analisada é caracterizada pela incerteza considerável e conhecimento incompleto. Desta forma, a lógica subjetiva torna-se uma lógica probabilística de probabilidades incertas. A vantagem é que a incerteza é realizada através da análise e é explicitado nos resultados de modo que é possível distinguir entre certas e incertas conclusões.
Redes confiáveis e redes Bayesianas são típicas aplicações da lógica subjetiva.
Redes confiáveis[editar | editar código-fonte]
Redes de confiança pode ser modelado com uma combinação de operadores de transitividade e de fusão. Seja expressar os cantos de confiança de to . Uma rede de confiança simples pode por exemplo se expressa como como ilustrado na figura ao lado.
Os índices 1, 2 e 3 indicam a ordem cronológica em que as margens de confiança e as recomendações são formadas. Assim, dado o conjunto de confiança bordas com índice 1, o confidente de origem recebe recomendações de e , e é assim apto a derivar confiança em . Ao expressar cada aresta confiança e recomendação como uma opinião 's confiança em pode ser computado como .
Redes de confiança pode expressar a fiabilidade das fontes de informação para as proposições, e pode ser usado para determinar opiniões subjetivas sobre proposições. Não pode haver uma rede de confiança separada levando à opinião sobre cada termo proposicional.
Redes Bayesianas[editar | editar código-fonte]
Na rede bayesiana baixo, e são quadros de evidência e é o quadro conclusão. As molduras podem ter cardinalidade arbitrário, e, no exemplo os quadros provas são ilustrados com cardinalidade 3. As opiniões condicionais expressam uma relação condicional entre os quadros de evidências e do quadro conclusão.
A evidência em e produz separadas opiniões derivadas em que é fundida com seus acumulativos ou aproximados operadores de fusão.
Referências
- ↑ a b c d A. Jøsang. Raciocínio Artificial com Lógica Subjetiva. Procedimentos do Segundo Workshop Australiano sobre Raciocínio de Senso Comum, Perth 1997. PDF
- ↑ a b c A. Jøsang. Uma lógica para probabilidades incertas. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems. 9(3), pp.279-311, Junho 2001. PDF
- ↑ a b c A. Jøsan. Probabilistic Logic Under Uncertainty. Proceedings of Computing: The Australian Theory Symposium (CATS'07), Ballarat, January 2007. PDF
- ↑ a b D. McAnally and A. Jøsang. Addition and Subtraction of Beliefs. Proceedings of the conference on Information Processing and Management of Uncertainty in Knowledge-Based Systems (IPMU2004), Perugia, July, 2004.
- ↑ a b c d e A. Jøsang, and D. McAnally. Multiplication and Comultiplication of Beliefs. International Journal of Approximate Reasoning, 38/1, pp.19-51, 2004.
- ↑ A. Jøsang, S. Pope and M. Daniel. Conditional Deduction Under Uncertainty. Proceedings of the 8th European Conference on Symbolic and Quantitative Approaches to Reasoning with Uncertainty (ECSQARU 2005). Barcelona, Spain, July 2005.
- ↑ a b A. Jøsang. Conditional Reasoning with Subjective Logic. Journal of multiple valued logic and soft computing (in press). 2008.PDF
- ↑ S. Pope and A. Jøsang. Analysis of Competing Hypothesis using Subjective Logic. Proceedings of the 10th International Command and Control Research Technology Symposium (ICCRTS'05), McLean Virginia, USA, 2005.
- ↑ a b A. Jøsang, S. Pope, and S. Marsh. Exploring Different Types of Trust Propagation. Proceedings of the 4th International Conference on Trust Management (iTrust'06), 2006.
- ↑ A. Jøsang. The Consensus Operator for Combining Beliefs. Artificial Intelligence Journal, 142(1-2), Oct. 2002, p.157-170
Ligações externas[editar | editar código-fonte]
- Online demonstrations[ligação inativa] da lógica subjetiva.












![{\displaystyle b,d,u,a\in [0,1]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7e91b6d912ed6cb9f89b714ae92e28b2bfc589e)



















![{\displaystyle {\vec {b}}(x_{i}),u,{\vec {a}}(x_{i})\in [0,1]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76016854e47ab6b2d891390258bcdd86aceb99ec)



















![{\displaystyle [A,B]:[B,C]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5bfa273ccb286eae277e2836dd4aefb312735fa)




![{\displaystyle [A,B]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/743c33f7e57c014a46b7bb338e95d1b12c2919f8)
![{\displaystyle ([A,B]:[B,D])\diamond ([A,C]:[C,D])\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5123464d8366679a8ee5aa79edcd6d4276f2490d)



