Polinômios de Legendre
Em matemática, os polinômios de Legendre são as soluções polinomiais da equação diferencial de Legendre:
para as quais .
Eles recebem esse nome em homenagem a Adrien-Marie Legendre. Esta equação diferencial ordinária é frequentemente encontrada na física e em outros campos técnicos. Em particular, ele surge na resolução da equação de Laplace (e equações diferenciais parciais) em coordenadas esféricas.
A equação diferencial de Legendre pode ser resolvida utilizando o método de série de potências usual. A equação possui um ponto singular regular em x= ± 1 então, em geral, uma solução com séries em relação a origem somente convergirá se |x| < 1. Quando n é um inteiro, a solução Pn(x) que é regular em x=1 é também regular em x=-1, e a série para esta solução é finita (i.e. é um polinômio).
Esta solução para n = 0, 1, 2,... (com a normalização Pn(1)=1) forma uma sequência polinomial de polinômios ortogonais chamados polinômios de Legendre. Cada polinômio de Legendre Pn(x) é um polinômio de n-ésimo grau. Isto pode ser expresso utilizando a fórmula de Rodrigues:
Propriedade de ortogonalidade[editar | editar código-fonte]
Uma importante propriedade dos polinômios de Legendre é a sua ortogonalidade com respeito ao produto interno L2 no intervalo −1 ≤ x ≤ 1:
(onde δmn denota o delta de Kronecker, igual a 1 se m = n e a 0 caso contrário). De facto, uma derivação alternativa dos polinômios de Legendre podem ser obtidas utilizando processo de Gram-Schmidt nos polinômios {1, x, x², ...} com respeito ao produto interno citado. O motivo dessa propriedade de ortogonalidade é que a equação diferencial de Legendre pode ser vista como um problema de Sturm-Liouville
onde os autovalores λ correspondem a n(n+1).
Exemplos dos polinômios de Legendre[editar | editar código-fonte]
Estes são os primeiros polinômios[1] de Legendre:
| n | |
| 0 | |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 |
Genericamente, tem-se (no caso de n ímpar, arredonda-se n/2 para baixo):
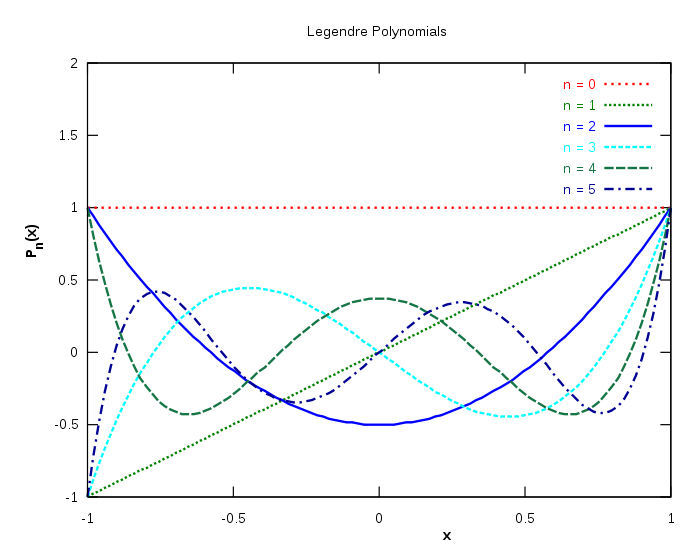
Os gráficos desses polinômios (até n = 5) são apresentados abaixo:
Aplicação dos polinômios de Legendre na física[editar | editar código-fonte]
Os polinômios de Legendre são úteis para expandir funções do tipo
onde e são os comprimentos dos vetores e respectivamente e é o ângulo entre esses dois vetores.
Esta expressão é usada, por exemplo, para obter o potencial de uma carga pontual sentida em um ponto enquanto esta carga está localizada no ponto . A expansão utilizando polinômios de Legendre pode ser útil quando se integra essa expressão sobre uma distribuição contínua de carga.
Os polinômios de Legendre ocorrem na solução da equação de Laplace do potencial elétrico, , em uma região do espaço sem cargas, utilizando o método de separação de variáveis, onde as condições de contornos possuem simetria axial (sem dependência com o ângulo azimutal). Onde é o eixo de simetria e é o ângulo entre a posição do observador e o eixo , a solução para o potencial será
e são determinados de acordo com as condições de contorno de cada problema.
Translação dos polinômios de Legendre[editar | editar código-fonte]
A translação dos polinômios de Legendre são definidos como sendo ortogonais no intervalo unitário [0,1]
Uma expressão explícita para estes polinômios é dada por
O análogo a fórmula de Rodrigues para a translação dos polinômios de Legendre é:
Ligações externas[editar | editar código-fonte]
- Eric W. Weisstein, Legendre Polynomial no MathWorld.
- «Wolfram MathWorld entry on Legendre polynomials»
- «Module for Legendre Polynomials by John H. Mathews»
Referências
- ↑ «Faça exemplos de qualquer grau com O Monitor». omonitor.io. Consultado em 23 de março de 2016

![{\displaystyle {d \over dx}\left[(1-x^{2}){d \over dx}P_{n}(x)\right]+n(n+1)P_{n}(x)=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd51c7228067db4bea119843fb19c6caab834954)

![{\displaystyle P_{n}(x)={1 \over 2^{n}n!}{d^{n} \over dx^{n}}\left[(x^{2}-1)^{n}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9414fbe11099d281205ca2a2f051f405c2d348c)

![{\displaystyle {d \over dx}\left[(1-x^{2}){d \over dx}P(x)\right]=-\lambda P(x),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a77762e99955d69860d114042e74d936005f6f1)












![{\displaystyle P_{n}(x)={1 \over 2^{n}n!}\sum _{k=0}^{n \over 2}\left[(-1)^{k}{n! \over k!(n-k)!}{(2n-2k)! \over (n-2k)!}x^{n-2k}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd440416e2de3414919131ac216e650b2d1caa2c)










![{\displaystyle \Phi (r,\theta )=\sum _{\ell =0}^{\infty }\left[A_{\ell }r^{\ell }+B_{\ell }r^{-(\ell +1)}\right]P_{\ell }(\cos \theta ).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4139ff9f97346ce5b7ffc3b6b2cbefe070298f3)





![{\displaystyle {\tilde {P_{n}}}(x)=(n!)^{-1}{d^{n} \over dx^{n}}\left[(x^{2}-x)^{n}\right].\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8ff98024276c11431068b42792c027a117df385)