Teorema Finito de Ramsey
Em combinatória, o Teorema de Ramsey diz que serão encontrados cliques monocromáticos em qualquer coloração de arestas de um grafo completo suficientemente grande. Para demonstrar o teorema para duas cores (por exemplo azul e vermelho), façamos r e s serem quaisquer inteiros positivos. O Teorema de Ramsey diz que existe um menor inteiro positivo R(r,s) para o qual toda coloração de arestas azul-vermelho de um grafo completo com R(r,s) vértices contem um clique azul em r ou um clique vermelho em s vértices. (Aqui R(r,s) significa um inteiro que depende de ambos r e s.)
O Teorema de Ramsey é um resultado fundacional em combinatória. A primeira versão desse resultado foi provada por F. P. Ramsey. Isso iniciou a teoria combinatória agora chamada de Teoria de Ramsey, que busca regularidade em meio a desordem: condições gerais para a existência de subestruturas com propriedades regulares. Nessa aplicação é uma questão da existência de subconjuntos monocromáticos, isto é, subconjuntos de arestas conectadas de apenas uma cor.
Uma extensão desse teorema se aplica para qualquer número finito de cores, ao invés de apenas duas. Mais precisamente, o teorema diz que para qualquer número de cores c, e quaisquer inteiros n1,...,nc, existe um número, R(n1, ..., nc), tal que se as arestas de um grafo completo de ordem R(n1, ..., nc) estão coloridas com c cores diferentes, então para algum i entre 1 e c, deve conter um subgrafo completo de ordem ni cujas arestas são todas cores i. O caso especial acima tem c = 2 (e n1 = r e n2 = s).
Exemplo: R(3,3) = 6[editar | editar código-fonte]
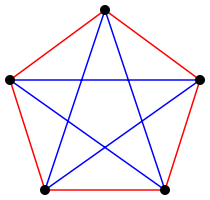
No caso 2-colorido, um grafo simples arbitrário G = (V, E) pode ser identificado com o grafo completo no conjunto de vértices V cujas arestas são coloridas com duas cores (todas as arestas correspondentes a arestas de E recebem uma cor e todas as outras recebem outra cor.) Isso permite falar sobre o Teorema de Ramsey usando a terminologia "conectado e "não-conectado" ao invés de cores, mas essa linguagem não generaliza para um maior número de cores. No exemplo a seguir a formula R(3,3) providencia uma solução para a questão que pede pelo menor número de vértices que um grafo deve conter para garantir que:
- ao menos 3 vértices no grafo são mutualmente conectados (formam um clique), ou
- ao menos 3 vértices no grafo são mutualmente desconectados (um conjunto independente).
O restante desse artigo vai usar a terminologia mais comum de cores e se referirá a cliques monocromáticos. Note que devido a natureza do espaço problema, R(r,s) é igual a R(s,r).
Suponha que as arestas de um grafo completo de 6 vértices são coloridas azul e vermelho. Escolha um vértice v. Existem 5 arestas incidentes a v e então (pelo Princípio da casa dos pombos) ao menos 3 deles devem ter a mesma cor. Sem perda de generalidade, podemos assumir que pelo menos 3 dessas arestas, conectando o vértice v aos vértices r, s e t, são azuis. (Senão, troque vermelho por azul no que se segue.) Se qualquer aresta (r, s), (r, t), (s, t) são também azuis, então temos um triângulo inteiramente azul. Senão, então essas três arestas são todas vermelhas e nós temos um triângulo inteiramente vermelho. Já que esse argumento funciona para qualquer colorimento, qualquer K6 contem um K3 monocromático, e portanto R(3,3) ≤ 6. A versão popular disso é chamada de teorema dos amigos e estranhos.
Uma prova alternativa usa contagem dupla. Funciona do seguinte modo: Conte o número de triplas ordenadas de vértices x, y, z tal que a aresta (xy) é vermelha e a aresta (yz) é azul. Primeiramente, qualquer vértice dado será o meio de 0 × 5 = 0 (todas as arestas do vértice tem a mesma cor), 1 × 4 = 4 (quatro da mesma cor, um de outra), ou 2 × 3 = 6 (três são da mesma cor, duas são de outra) tais triplas. Portanto existem no máximo 6 × 6 = 36 tais triplas. Seguidamente, para qualquer triangulo não-monocromático (xyz), existem precisamente duas triplas. Portanto existem no máximo 18 triângulos não-monocromáticos. Desse modo, ao menos 2 dos 20 triângulos em K6 são monocromáticos.
Reciprocamente, é possível 2-colorir um K5 sem criar qualquer K3 monocromático, mostrando que R(3,3) > 5. A única coloração é mostrada a direita. Então R(3,3) = 6.
A tarefa de provar que R(3,3) ≤ 6 foi um dos problemas da Competição Putnam em 1953.
Números de Ramsey[editar | editar código-fonte]
Os números R(r, s) no teorema de Ramsey ( e suas extensões para mais de duas cores) são conhecidos como números de Ramsey. Um limite superior para R(r, s) pode ser extraído do teorema de prova, e outros argumentos dão o limite inferior. (O primeiro limite inferior foi obtido por Paul Erdős usando o método probabilístico.) Entretanto, existe um vasto intervalo entre os limites inferiores mais próximos e os limite superiores mais próximos. Existem também poucos números r e s para os quais sabemos o exato valor de R(r, s). Computar um limite inferior L para R(r, s) geralmente requer exibir uma coloração azul/vermelha do grafo KL−1 sem nenhum subgrafo azul Kr e nenhum subgrafo vermelho Ks. Limites superiores são comummente mais difíceis de se estabelecer: deve-se checar todas as possíveis colorações possíveis para confirmar a ausência de um contra-exemplo, ou apresentar um argumento matemático para sua ausência. Um programa de computador sofisticado não precisa olhar todas as colorações possíveis individualmente para eliminar todas elas; de toda forma é uma tarefa computacional difícil que softwares atuais só realizam em pequenas amostras. Cada grafo completo Kn tem 12(n)(n − 1) arestas, então haveria um total de c(n)(n−1)2 para se checar (para c cores) se força bruta fosse usada.[1] Portanto, a complexidade de se checar todos os possíveis grafos (via força bruta) é O(cn2) para c colorações e um limite superior de n vértices.
Como descrito acima, R(3, 3) = 6. É fácil de mostrar que R(4, 2) = 4, e, mais geralmente, que para todos R(s, 2) = s s: um grafo com s − 1 nós com todas as arestas de cor vermelha serve como um contra-exemplo e prova que R(s, 2) ≥ s; entre colorações de um grafo sobre s nós, a coloração com todas as arestas de cor vermelha contém um subgrafo com s nós vermelhos, e todas as outras colorações contem um subgrafo azul com 2 - nós(isto é, um par de nós ligados com uma aresta azul.) Usando as desigualdades de indução, pode concluir-se que R(4, 3) ≤ R(4, 2) + R(3, 3) − 1 = 9, e, por conseguinte, R(4, 4) ≤ R(4, 3) + R(3, 4) ≤ 18.
Existem apenas dois grafos (4, 4, 16) (isto é, 2-colorações de um grafo completo com 16 nós sem subgrafos completos com 4-nós vermelhos ou azuis) entre 6.4 × 1022 diferentes 2- colorações de grafos com 16, e apenas um (4, 4, 17) grafo (o Grafo de Paley da ordem
| Parte da série sobre | ||
| Matemática | ||
|---|---|---|
|
||
) entre 2.46 × 1026 colorações[2] (Isso foi comprovado por Evans, Pulham e Sheehan em 1979.) Segue-se que R(4, 4) = 18.
O fato de que R(4, 5) = 25 foi estabelecido por Brendan McKay e Stanisław Radziszowski em 1995.[3]
O valor exato de R(5, 5) é desconhecida, embora se saiba que se encontra entre 43 (Geoffrey Exoo) e 49 (McKay e Radziszowski) (inclusive).
| “ | Erdős nos pede para imaginar uma força alienígena, muito mais poderosa do que nós, desembarcando na Terra e exigindo o valor de R(5, 5) ou eles vão destruir o nosso planeta. Nesse caso, ele afirma, devemos mobilizar todos os nossos computadores e todos os nossos matemáticos e tentar encontrar o valor. Mas suponha que, em vez disso, que eles pedem R(6, 6). Nesse caso, ele acredita, devemos tentar destruir os aliens | ” |
Em 1997 McKay, Radziszowski e Exoo empregaram métodos de geração de gráfo assistida por computador para conjecturar que R(5, 5) = 43. Eles foram capazes de construir exatamente 656 grafos (5, 5, 42), chegando ao mesmo conjunto de grafos através de diferentes rotas. Nenhum dos 656 grafos pode ser estendido para um grafo (5, 5, 43).[5]
Para R(r, s) com r, s > 5, apenas limites fracos são disponíveis. Limites inferiores para R(6, 6) e R(8, 8) não foram melhoradas desde 1965 e 1972, respectivamente.[6]
R(r, s) com r, s ≤ 10} são mostrados na tabela abaixo . Sempre que o valor exato é desconhecido, a tabela lista os limites mais conhecidos. R(r, s) com r, s < 3 são dados por R(1, s) = 1 e R(2, s) = s para todos os valores de s. A pesquisa padrão sobre desenvolvimento de pesquisa de número de Ramsey foi escrito por Stanisław Radziszowski.
| r,s | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | |||||||||
| 2 | 1 | 2 | ||||||||
| 3 | 1 | 3 | 6 | |||||||
| 4 | 1 | 4 | 9 | 18 | ||||||
| 5 | 1 | 5 | 14 | 25 | 43–49 | |||||
| 6 | 1 | 6 | 18 | 36–41 | 58–87 | 102–165 | ||||
| 7 | 1 | 7 | 23 | 49–61 | 80–143 | 113–298 | 205–540 | |||
| 8 | 1 | 8 | 28 | 58–84 | 101–216 | 132–495 | 217–1031 | 282–1870 | ||
| 9 | 1 | 9 | 36 | 73–115 | 126–316 | 169–780 | 241–1713 | 317–3583 | 565–6588 | |
| 10 | 1 | 10 | 40–42 | 92–149 | 144–442 | 179–1171 | 289–2826 | 331–6090 | 581–12677 | 798–23556 |
Como R(r, s) = R(s, r), há é uma simetria trivial entre a diagonal.
Esta tabela é extraída de uma tabela maior compilado por Stanisław Radziszowski.[6]
Assintótica[editar | editar código-fonte]
A desigualdade R(r, s) ≤ R(r − 1, s) + R(r, s − 1) pode ser aplicada para provar indutivamente que
Em particular, este resultado, devido a Erdős e Szekeres, implica que quando r = s,
Um limite inferior exponencial,
foi dado por Erdős em 1947 e foi instrumental em sua introdução do método probabilístico. Há obviamente uma enorme lacuna entre esses dois limites: por exemplo, para s = 10, isto dá 101 ≤ R(10, 10) ≤ 48620. No entanto, fatores de crescimento exponencial de qualquer limite não tem sido melhorados até hoje e ainda se mantem a 4 e √2, respectivamente. Não se conhece qualquer construção explícita produzindo um limite inferior exponencial . Os mais conhecidos limites inferior e superior para números de Ramsey diagonais atualmente estão em
graças a Spencer and Conlon respectively.
Para os números de Ramsey fora da diagonal R(3, t), sabe-se que eles são de ordem ; isso pode ser declarado de forma equivalente a dizer que o menor possível [Conjunto Independente [(teoria dos grafos) | número independênte]] em um gráfo livre de triângulo de n vértices é
O limite superior para R(3, t) é dada por Ajtai, Komlós e Szemerédi, o limite inferior por Kim. De modo mais geral, para os números de Ramsey fora da diagonal R(s, t) com s fixa e t crescendo, os limites mais conhecidos são
devido a Bohman e Keevash e Ajtai, Komlós e Szemerédi, respectivamente.
Um exemplo multicolorido: R(3,3,3) = 17[editar | editar código-fonte]

Um número multicor Ramsey é um número Ramsey usando três ou mais cores. Existe apenas um número Ramsey multicor não trivial para os quais o valor exato é conhecido, ou seja, R (3,3,3) = 17.
Suponha que você tem uma coloração de arestas de um grafo completo usando três cores, vermelho, amarelo e verde. Suponha ainda que a coloração de arestas não tem triângulos monocromáticos. Selecione um vértice v . Considere o conjunto de vértices que têm uma aresta verde para o vértice v . Isso é chamado de bairro verde de v . O bairro verde de v não pode conter quaisquer arestas verdes, pois, caso contrário haveria um triângulo verde, composto pelos dois pontos da aresta verde e o vértice v . Assim, a coloração induzida da aresta no bairro verde de v tem arestas coloridas com apenas duas cores, ou seja, amarelo e vermelho. Como R (3,3) = 6, o bairro verde de v pode conter, no máximo, 5 vértices. Da mesma forma, os bairros vermelhos e amarelos do v pode conter, no máximo, cinco vértices cada. Uma vez que cada vértice, com exceção de v em si, está em um dos bairros verdes, vermelhas ou amarelas de v , todo o grafo completo pode ter, no máximo, 1 + 5 + 5 + 5 = 16 vértices. Assim, temos R (3,3,3) ≤ 17.
Para ver que R (3,3,3) ≥ 17, basta desenhar uma coloração de arestas no grafo completo em 16 vértices com 3 cores que evita triângulos monocromáticos. Acontece que há exatamente duas dessas colorações no K 16 , as chamadas colorações não torcidos e torcidos. Ambas as colorações estão apresentados na figura para a direita, com a coloração sem torção na parte superior, e a coloração torcida na parte inferior. Em ambas as colorações na figura, note que os vértices são rotulados, e que os vértices V 11 até v 15 são atraídos por duas vezes, tanto à esquerda como à direita, a fim de simplificar os desenhos.
Assim, R(3,3,3) = 17.
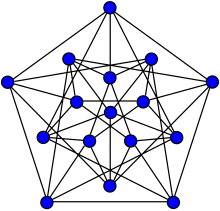
Se você selecionar qualquer cor ou a coloração sem torção ou torcida em K 16 , e considerar o gráfico cujas bordas são precisamente essas arestas que têm a cor especificada, você vai ter o Grafo de Clebsch.
Sabe-se que há exatamente duas colorações de arestas com três cores em K 15 que evitam triângulos monocromáticos, que podem ser construídos deletando qualquer vértice das colorações não torcidas e torcida em K 16 , respectivamente.
Sabe-se também que existem exatamente 115 colorações de arestas com 3 cores em K 14 que evitam triângulos monocromáticos, desde que se considere colorações de aresta que diferem por uma permutação das cores como sendo a mesma.
Extensões do teorema[editar | editar código-fonte]
O teorema também pode ser estendido para hipergrafos. Um m-hipergrafo é um gráfo cujas "arestas" são conjuntos de m vértices - em um gráfo normal uma aresta é um conjunto de dois vértices. A declaração completa de teorema de Ramsey para hipergrafos é que, para quaisquer inteiros m e c, e quaisquer inteiros n 1 , ..., n' 'c' ', existe um inteiro R(n1, ..., nc;c,m) de modo que se as hiperarestas de um m-hipergrafos completo de ordem R (n 1 , ..., n c ; c, M) são coloridos com c cores diferentes, então por algum i entre 1 e c, o hipergrafo deve conter um completo sub-m-hipergrafo de ordem ni cujas hiperarestas são todas de cor i. Este teorema é normalmente provado por indução sobre m, a 'hiper-nesa" do grafo. O caso base para a prova é m = 2, que é exatamente o teorema acima.
Teorema Infinito Ramsey[editar | editar código-fonte]
Um outro resultado, também comumente chamado de teorema de Ramsey , aplica-se a grafos infinitos. Num contexto em que grafos finitos também estão sendo discutidas muitas vezes é chamado de " Teorema Infinito Ramsey". Como a intuição pela representação pictórica de um grafo é diminuída quando se deslocam de finito para grafos infinitos, teoremas nesta área são geralmente redigidas na Teoria dos conjuntos na terminologia.[7]
Teorema. Faça X ser um conjunto infinito contavel e pinte os elementos de X(n) (os subconjuntos de X de tamanho n) em c cores diferentes. Então existem alguns subconjuntos M de X tal que os subconjunto de tamanho n de M possuem todos a mesma cor.
Prova: A prova é por indução em n, o tamanho dos subconjuntos. Para n = 1, a afirmação é equivalente a dizer que se você dividir um conjunto infinito em um número finito de conjuntos, então, um deles é infinito. Isto é evidente. Assumindo que o teorema é verdadeiro para n ≤ r, provamos para n = r + 1. Dado uma c-coloração do subconjunto de (r + 1)-elementos de X , fazendo a0 ser um elemento de X e deixe Y = X\{a0}. Em seguida, induzimos uma c- coloração do subconjuntos de r - elementos de Y , apenas adicionando a0 para cada subconjuntos de r - elementos (para obter um subconjunto de (r + 1)- elementos de X ). Pela hipótese de indução, existe um subconjunto infinito Y1 de Y de modo a que cada subconjunto com r-elementos de Y1 é colorido da mesma cor na coloração induzida. Assim, existe um elemento a0 e um subconjunto infinito Y1 de tal modo que todo subconjunto de (r + 1)-elementos de X que consiste em a0 e r elementos de Y1 têm a mesma cor. Pelo mesmo argumento, há um elemento a1 em Y1 e um subconjunto infinito Y2 de Y1 com as mesmas propriedades. Indutivamente, obtemos a sequencia {a0,a1,a2,...} de forma que a cor de cada subconjunto (r + 1)-elementos (ai(1),ai(2),...,ai(r + 1)) com i(1) < i(2) < ... < i(r + 1) depende apenas do valor de i(1).Além disso, há um número infinito de valores de i(n) de tal modo que esta cor será a mesmo. Use os ai(n)'s para obter o conjunto monocromático desejado.
Versão infinita implica a finita[editar | editar código-fonte]
É possível deduzir o teorema finito de Ramsey através da versão infinita por uma prova por contradição. Suponha que o teorema finito de Ramsey é falso. Então, existem inteiros c, n, T tal que, para todo inteiro k, existe uma ccoloração de sem um conjunto monocromático de tamanho T. Seja Ck a c-coloração de sem um conjunto monocromático de tamanho T.
Para qualquer k, a restrição da coloração em Ck+1 para (ignorando a cor de todos os conjuntos contendo k+1) e a coloração em Ck os quais são restrições de coloração em Ck+1. Desde que Ck+1 não seja vazio, também não é.
De maneira semelhante, a restrição de qualquer coloração em , está em , permitindo definir como sendo o conjunto de todas essas restrições, um conjunto não-vazio. Continuando assim, define-se para todos os inteiros m, k.
Para qualquer inteiro k, , e cada conjunto é não-vazio. Além disso Ck é infinito como . Segue-se que a interseção de todos esses conjuntos e não-vazia, e permitem . Então, toda coloração em Dk é a restrição de uma coloração em Dk+1. Logo, por tornar não restrita uma coloração em Dk para uma coloração em Dk+1, e continuando a fazer isso, constrói-se uma coloração de sem nenhum conjunto monocromático de tamanho T. Isto contradiz o teorema infinito de Ramsey
Se um ponto de vista topológico adequado e tomado, este argumento se torna um argumento da compacidade padrão, mostrando que a versão infinita do teorema implica na versão finita.
Grafo direcionado com Números de Ramsey[editar | editar código-fonte]
É possível, também, definir números de Ramsey para grafos direcionados. (Estes foram introduzidos por P. Erdős & L. Moser.) Seja R(n) o menor número Q tal que, qualquer grafo completo com arcos unidirecionais (também chamado de torneio) e com ≥ Q nós contem um acíclico (também chamado "transitivo") "n"-nó subtorneio.
Este é o grafo direcionado análogo ao que foi chamado (acima) R(n,n;2), o menor número Z tal que qualquer 2-coloração das bordas de um grafo completo nãodirecionado com ≥ Z nós, contem um grafo completo monocromático em n nós. (o análogo dirigido das duas possíveis cores de arco, são as duas direções dos arcos, o análogo de "monocromático" é "toos os ponteiros de arco apontam na mesma direção" i.e. "acíclico.")
De fato, muitos acham o problema do grafo dirigido mais elegante do que o não-dirigido. Nos temos queR(0)=0, R(1)=1, R(2)=2, R(3)=4, R(4)=8, R(5)=14, R(6)=28, 32≤R(7)≤55, e R(8) são novamente um problema, de acordo com Erdős.
Ver também[editar | editar código-fonte]
Notas[editar | editar código-fonte]
Referências
- ↑ 2.6 Ramsey Theory from Mathematics Illuminated
- ↑ «Ramsey Graphs»
- ↑ Brendan D. McKay, Stanislaw P. Radziszowski (maio de 1995). «R(4,5) = 25». Journal of Graph Theory. doi:10.1002/jgt.3190190304
- ↑ Joel H. Spencer (1994), Ten Lectures on the Probabilistic Method, ISBN 978-0-89871-325-1, SIAM, p. 4
- ↑ Brendan D. McKay, Stanisław P. Radziszowski. «Subgraph Counting Identities and Ramsey Numbers» (PDF). Journal of Combinatorial Theory
- ↑ a b «Dynamic Surveys»
- ↑ Martin Gould. «Ramsey Theory» (pdf)
- Ajtai, Miklós; Komlós, János; Szemerédi, Endre (1980), «A note on Ramsey numbers», J. Combin. Theory Ser. A, 29 (3): 354–360, doi:10.1016/0097-3165(80)90030-8.
- Bohman, Tom; Keevash, Peter (2010), «The early evolution of the H-free process», Invent. Math., 181 (2): 291–336, doi:10.1007/s00222-010-0247-x.
- Conlon, D. (2009), «A new upper bound for diagonal Ramsey numbers», Annals of Mathematics, 170 (2): 941–960, doi:10.4007/annals.2009.170.941.
- Do, Norman (2006). «Party problems and Ramsey theory» (PDF). Austr. Math. Soc. Gazette. 33 (5): 306–312
- Erdős, Paul (1947), «Some remarks on the theory of graphs», Bull. Amer. Math. Soc., 53 (4): 292–294, doi:10.1090/S0002-9904-1947-08785-1.
- Erdős, Paul; Szekeres, George (1935), «A combinatorial problem in geometry», ISBN 978-0-8176-4841-1, Compositio Mathematica, 2: 463–470, doi:10.1007/978-0-8176-4842-8_3.
- Exoo, G. (1989), «A lower bound for R(5,5)», Journal of Graph Theory, 13: 97–98, doi:10.1002/jgt.3190130113.
- Graham, R.; Rothschild, B.; Spencer, J. H. (1990), Ramsey Theory, New York: John Wiley and Sons.
- Ramsey, F. P. (1930), «On a problem of formal logic», Proceedings of the London Mathematical Society, 30: 264–286, doi:10.1112/plms/s2-30.1.264.
- Spencer, J. (1975), «Ramsey's theorem – a new lower bound», J. Combin. Theory Ser. A, 18: 108–115, doi:10.1016/0097-3165(75)90071-0.
- Bian, Zhengbing; Chudak, Fabian; Macready, William G.; Clark, Lane; Gaitan, Frank (2013), «Experimental determination of Ramsey numbers», Physical Review Letters, 111: 130505-1 - 130505-6, Bibcode:2013PhRvL.111m0505B, doi:10.1103/PhysRevLett.111.130505.
Ligações externas[editar | editar código-fonte]
- Hazewinkel, Michiel, ed. (2001), «Ramsey theorem», Enciclopédia de Matemática, ISBN 978-1-55608-010-4 (em inglês), Springer
- Ramsey@Home is a distributed computing project designed to find new lower bounds for various Ramsey numbers using a host of different techniques.
- Radziszowski's survey of small Ramsey numbers
- Lisp code to compute upper bounds for particular Ramsey numbers given the general rules in Radziszowski
- Survey of directed-graph Ramsey numbers
- Ramsey Number – from MathWorld (contains lower and upper bounds up to R(19,19))
- Ramsey Number – Geoffrey Exoo (Contains R(5,5) > 42 counter-proof)








![{\displaystyle [k]^{(n)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42d930048b86ff67b9218b289406b5767f6e47b8)








