Usuário(a):Jformighi/Gráfico de uma função

Gráfico da função$f(x)={\frac {x^{3}+3x^{2}-6x-8}{4}}.$

Em matemática, o gráfico de uma função $f$ é o conjunto de pares ordenados $(x,y)$, onde $f(x)=y.$ No caso comum em que $x$ e $f(x)$ são números reais, estes pares são coordenadas cartesianas de pontos no espaço bidimensional e formam assim um subconjunto deste plano.

No caso de funções de duas variáveis, são funções cujo domínio consiste em pares $(x,y),$ o gráfico geralmente se refere ao conjunto de triplos ordenados $(x,y,z)$ onde $f(x,y)=z,$ em vez dos pares $((x,y),z)$ como na definição acima. Este conjunto é um subconjunto do espaço tridimensional, para uma função contínua de valor real de duas variáveis reais, é uma superfície .

O gráfico de uma função é a fotografia que essa função possui. Através do gráfico, podemos definir de que tipo é a função mesmo sem saber qual é a sua lei de formação. Isso porque cada função tem sua representação gráfica de forma específica. Na matemática, ciência, engenharia, tecnologia, finanças e outras áreas, os gráficos são ferramentas utilizadas para diversos fins. No caso mais simples, uma variável é plotada em função de outra, normalmente usando sistema de coordenadas cartesiano.

Um gráfico de uma função é um caso especial de relação. Nos fundamentos modernos da matemática, e, tipicamente, na teoria dos conjuntos, uma função é na verdade igual ao seu gráfico. No entanto, muitas vezes é útil ver funções como mapeamentos, que consistem não apenas na relação entre entrada e saída, mas também em qual conjunto é o domínio e qual conjunto é o contradomínio .

Por exemplo, dizer que uma função é sobrejetora ou não o contradomínio deve ser levado em consideração. O gráfico de uma função por si só não determina o contradomínio. É comum utilizar os termos função e gráfico de uma função, pois mesmo sendo considerados o mesmo objeto, indicam uma perspectiva diferente de representar uma relação matemática entre variáveis.

Gráfico da função $f(x)=x^{4}-4^{x}$ no intervalo [−2,+3]. Também são mostradas as duas raízes reais e seu intervalo.

Definição

Dada uma função $f:X\to Y,$ em outras palavras, uma função $f$ com seu domínio $X$ e contradomínio $Y,$ o gráfico será o conjunto

$$G(f)=\{(x,f(x)):x\in X\},$$

que é um subconjunto de $X\times Y$ . Na definição abstrata de uma função, $G(f)$ é igual a $f.$

Pode-se observar que, se, $f:\mathbb {R} ^{n}\to \mathbb {R} ^{m},$ então o gráfico $G(f)$ é um subconjunto de $\mathbb {R} ^{n+m}$ (estritamente falando é $\mathbb {R} ^{n}\times \mathbb {R} ^{m},$ mas pode-se incorporá-lo ao isomorfismo natural).

Exemplos

Funções de uma variável

Gráfico da função$f(x,y)=\sin \left(x^{2}\right)\cdot \cos \left(y^{2}\right).$

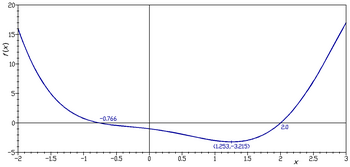
O gráfico da função $f:\{1,2,3\}\to \{a,b,c,d\}$ definido por:

$$f(x)={\begin{cases}a,&{\text{if }}x=1,\\d,&{\text{if }}x=2,\\c,&{\text{if }}x=3,\end{cases}}$$

é o subconjunto do conjunto $\{1,2,3\}\times \{a,b,c,d\}$

$$G(f)=\{(1,a),(2,d),(3,c)\}.$$

No gráfico, o domínio $\{1,2,3\}$ é dado como o conjunto do primeiro componente de cada par no gráfico $\{1,2,3\}=\{x:\ \exists y,{\text{ tal que }}(x,y)\in G(f)\}$. Da mesma forma, o intervalo pode ser dado como $\{a,c,d\}=\{y:\exists x,{\text{ tal que }}(x,y)\in G(f)\}$ . O contradomínio $\{a,b,c,d\}$, no entanto, não pode ser determinado apenas pelo gráfico.

O gráfico do polinômio cúbico na reta real

$$f(x)=x^{3}-9x$$

é

$$\{(x,x^{3}-9x):x\in \mathbb {R} \}.$$

Se este conjunto for traçado num plano cartesiano, o resultado é uma curva (ver figura).

Funções de duas variáveis

Plotagem do gráfico da função, $f(x,y)=-\left(\cos \left(x^{2}\right)+\cos \left(y^{2}\right)\right)^{2},$mostrando também seu gradiente projetado no plano inferior.

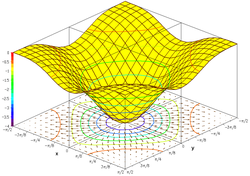
O gráfico da função trigonométrica

$$f(x,y)=\sin(x^{2})\cos(y^{2})$$

é

$$\{(x,y,\sin(x^{2})\cos(y^{2})):x{\text{ e }}y{\text{ são números reais}}\}.$$

Se este conjunto for plotado em um sistema de coordenadas cartesianas tridimensional, o resultado é uma superfície (ver figura).

Muitas vezes é útil mostrar com o gráfico o gradiente da função e várias curvas de nível. As curvas de nível podem ser mapeadas na superfície funcional ou projetadas no plano inferior. A segunda figura mostra um desenho do gráfico da função:

$$f(x,y)=-(\cos(x^{2})+\cos(y^{2}))^{2}.$$