Círculo de Mohr
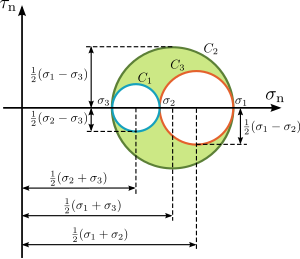
O círculo de Mohr, denominado em memória de seu idealizador, Christian Otto Mohr, é um método gráfico bidimensional representativo da lei de transformação do tensor tensão de Cauchy.
Após realizar uma análise de tensões em um corpo material assumido como um meio contínuo, as componentes do tensor tensão de Cauchy em um determinado ponto do corpo são conhecidas em relação a um sistema de coordenadas. O círculo de Mohr é então usado para determinar graficamente as componentes de tensão em relação a um sistema rotacionado, isto é, agindo sobre um plano de orientação diferente passando sobre o ponto.
A abscissa e a ordenada de cada ponto do círculo são as magnitudes da tensão normal e da tensão cisalhante atuando sobre um sistema de coordenadas rotacionado. Em outras palavras, o círculo é o locus dos pontos que representam o estado de tensão sobre planos individuais em todas as suas orientações, onde os eixos representam os eixos principais dos elementos de tensão.
Karl Culmann foi o primeiro a conceber uma representação gráfica para tensões, considerando tensões normais e cisalhantes em vigas horizontais sob flexão. A contribuição de Mohr estendeu o uso desta representação para estados de tensão bi e tridimensional e desenvolveu um critério de falha baseado sobre o círculo de tensão.[1]
O círculo de Mohr pode ser aplicado a qualquer matriz simétrica 2x2, incluindo os tensores deformação e momento de inércia.
Motivação[editar | editar código-fonte]

Forças internas são produzidas entre as partículas de um objeto deformável, assumido como um continuum, em reação às forças externas aplicadas, ou seja, tanto as forças de superfície quanto as forças de corpo. Esta reação resulta das leis do movimento de Euler para um continuum, que são equivalentes às leis do movimento de Newton para uma partícula. Uma medida da intensidade destas forças internas é chamada de tensão. Como o objeto é assumido como um contínuo, estas forças internas são distribuídas de forma contínua dentro do volume do mesmo.
Bibliografia[editar | editar código-fonte]
- Beer, Ferdinand Pierre; Elwood Russell Johnston; John T. DeWolf (1992). Mechanics of Materials. [S.l.]: McGraw-Hill Professional. ISBN 0-07-112939-1
- Brady, B.H.G.; E.T. Brown (1993). Rock Mechanics For Underground Mining Third ed. [S.l.]: Kluwer Academic Publisher. pp. 17–29. ISBN 0-412-47550-2
- Davis, R. O.; Selvadurai. A. P. S. (1996). Elasticity and geomechanics. [S.l.]: Cambridge University Press. pp. 16–26. ISBN 0-521-49827-9
- Holtz, Robert D.; Kovacs, William D. (1981). An introduction to geotechnical engineering. Col: Prentice-Hall civil engineering and engineering mechanics series. [S.l.]: Prentice-Hall. ISBN 0-13-484394-0
- Jaeger, John Conrad; Cook, N.G.W; Zimmerman, R.W. (2007). Fundamentals of rock mechanics Fourth ed. [S.l.]: Wiley-Blackwell. pp. 9–41. ISBN 0-632-05759-9
- Jumikis, Alfreds R. (1969). Theoretical soil mechanics: with practical applications to soil mechanics and foundation engineering. [S.l.]: Van Nostrand Reinhold Co. ISBN 0-442-04199-3
- Parry, Richard Hawley Grey (2004). Mohr circles, stress paths and geotechnics 2 ed. [S.l.]: Taylor & Francis. pp. 1–30. ISBN 0-415-27297-1
- Timoshenko, Stephen P.; James Norman Goodier (1970). Theory of Elasticity Third ed. [S.l.]: McGraw-Hill International Editions. ISBN 0-07-085805-5
- Timoshenko, Stephen P. (1983). History of strength of materials: with a brief account of the history of theory of elasticity and theory of structures. Col: Dover Books on Physics. [S.l.]: Dover Publications. ISBN 0-486-61187-6
Referências
- ↑ Parry, Richard Hawley Grey (2004). Mohr circles, stress paths and geotechnics 2 ed. [S.l.]: Taylor & Francis. pp. 1–30. ISBN 0-415-27297-1


