Fenómeno de Runge

A curva vermelha é a Função de Runge.
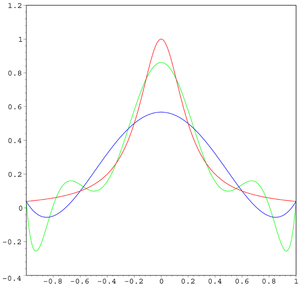
A curva azul é uma interpolação polinomial de 5ª ordem (usando seis pontos de interpolação igualmente espaçados).
A curva verde é uma interpolação polinomial de 9ª ordem (usando dez pontos de interpolação igualmente espaçados).
Nos pontos de interpolação, o erro entre a função e a interpolação polinomial é, por definição, zero entre os pontos de interpolação (especialmente na região próxima dos pontos 1 e -1) o erro entre a função e a interpolação polinomial aumenta para polinomiais de maior ordem.

Em matemática, em particular no campo específico da análise numérica, o fenômeno de Runge é um problema de oscilação nas bordas de um intervalo, que ocorre quando se usa interpolação polinomial com polinómios de ordem elevada. Foi descoberto por Carl Runge quando investigava erros na interpolação polinomial para aproximar certas funções. O fenômeno é similiar ao fenômeno de Gibbs para aproximações em séries de Fourier.

Introdução

O teorema da aproximação de Stone-Weirstrass afirma que toda função contínua f(x) definida em um intervalo [a,b] pode ser aproximada tanto quanto o desejado, por uma função polinomial P_n(x) de grau ≤ n, i.e.,

$\lim _{n\rightarrow \infty }\left(\max _{a\leq x\leq b}|f(x)-P_{n}(x)|\right)=0.$

A interpolação em pontos equidistantes é uma abordagem natural para construir polinomiais de aproximação. Porém, o fenômeno de Runge demonstra que interpolações podem facilmente resultar em uma sequência de aproximações divergente.

Problema

Considere a função:

$f(x)={\frac {1}{1+25x^{2}}}$

Runge descobriu que se fizermos a interpolação desta função em pontos equidistantes entre -1 e 1 tais que:

$x_{i}=-1+(i-1){\frac {2}{n}},i\in \left\{1,2,\cdots ,n+1\right\}$

com o polinómio $P_{n}(x)$ que tem grau $\leq n$, a resultante interpolação iria oscilar junto às extremidades do intervalo, ou seja, perto de -1 e 1. Pode mesmo ser provado que o erro de interpolação tende para infinito quando o grau do polinómio aumenta:

$\lim _{n\rightarrow \infty }\left(\max _{-1\leq x\leq 1}|f(x)-P_{n}(x)|\right)=\infty$

Soluções para o problema do fenômeno de Runge

A oscilação pode ser minimizada usando-se os nódulos de Chebyshev em vez de nódulos equidistantes. Neste caso, o erro máximo diminui quando a ordem do polinômio aumenta.

O fenômeno demonstra que polinômios de grau elevado são normalmente pouco recomendáveis para a interpolação. O problema pode ser evitado usando curvas spline, compostas de polinômios. Quando se tenta diminuir o erro de interpolação podemos aumentar o número de segmentos usados para construir a spline, em vez de aumentar o grau do polinômio.

Ver também

• Comparar com o fenômeno de Gibbs para funções de base senoidal.