Série de Fourier
Série de Fourier é uma forma de série trigonométrica usada para representar funções infinitas e periódicas complexas dos processos físicos, na forma de funções trigonométricas simples de senos e cossenos.[1][2] Isto é, simplificando a visualização e manipulação de funções complexas.[3] Foi criada em 1807 por Jean Baptiste Joseph Fourier (1768-1830).[3]
A forma geral da série é:[1]
em que os coeficiente , e são números que variam de acordo com a função que será representada, de período fundamental . Esses coeficientes são as amplitudes de cada onda em série,[2] que são calculadas com as seguintes fórmulas:[1]
A Série de Fourier é importante na técnica de compactação digital, como por exemplo: para reproduzir músicas digitais por streaming, para ver imagens online de rápido carregamento, e no cancelamento de ruído nos fones de ouvido.[4]

História[editar | editar código-fonte]
A série surgiu na tentativa de Fourier solucionar um problema físico, que gerou novas fronteiras na matemática.[3] Durante o estudo da propagação de calor em corpos sólidos. Admitindo que essa propagação deveria se por ondas de calor, levando em consideração que a forma mais simples de uma onda é uma função senoidal.[3][4] Assim Fourier demonstra através da transformada que qualquer função complexa, pode ser decomposta em uma combinação infinita de senoides,[4] dividida como uma soma de senos e cossenos.[2][3]
A ideia de decompor funções arbitrárias em termos de funções trigonométricas simples movimentou grandes nomes da matemática começando por volta de 1750 com L. Euler (1707-1783) e D. Bernoulli (1700-1782), seguindo com J. d'Alembert (1717-1783) e J. L. Lagrange (1736-1813).[5]
Mais tarde Jean-Baptiste Joseph Fourier (1768-1830) estudou sistematicamente tais séries infinitas, na tentativa de resolver a equação do calor. Em 1811, em sua Théorie mathématique de la chaleur (Teoria matemática de condução do calor), Fourier explicitou os coeficientes de tais séries (que ficaram conhecidos como coeficientes de Fourier, embora Euler já conhecesse o formato dos mesmos) e escreveu as séries de senos e cossenos de várias funções. De um ponto de vista moderno, os resultados de Fourier, embora muito importantes a forma da série que recebeu o seu nome, são informais, em boa parte devido à falta de uma definição concisa de funções e integrais até o início do século XIX.[6]
P. G. Dirichlet (1805-1859) foi um dos primeiros a reconhecer que nem toda função poderia ser representada por uma série de Fourier (fato que Fourier acreditava), obtendo uma condição suficiente para a validade da representação a partir da série estudada. Em um trabalho de 1829, Dirichlet dá a primeira demonstração rigorosa de que a série de Fourier de uma função f converge, em cada ponto x, para a média aritmética dos limites laterais de f nesse ponto. Nesse trabalho Dirichlet dá origem ao conceito de função como hoje se é conhecido.[5]
Aparentemente por influência de Dirichlet, G. B. Riemann (1826-1866) se interessou pelo estudo das séries trigonométricas, sendo levado a estudar a integral que leva hoje o seu nome e publicando em 1854 um trabalho intitulado "Sobre a representação de funções por meio de séries trigonométricas".[5]
Em 1876 du Bois-Reymond (1818-1896) construiu função cuja série de Fourier divergia em um dado ponto, e mais tarde ele mesmo construiu uma função cuja série divergia em um conjunto denso. Exemplos mais simples foram dados por L. Fejér (1880 -1959) em 1909. Vale citar também que em 1861 K. Weierstrass (1815-1897) deu o primeiro exemplo de função contínua sem derivada em ponto algum, sendo tal função definida por uma série trigonométrica que converge uniformemente (portanto uma série de Fourier).[6]
Não esqueçamos de citar G. Cantor (1845-1918), o qual teve grande influência pelo trabalho de Dirichlet e investigou o problema da unicidade da representação de funções por séries trigonométricas. Tais influências foram decisivas para a definição de números reais como sequência de números racionais e para a criação da Teoria dos Conjuntos, o que mostra o quão importante para o desenvolvimento da fundamentação teórica da matemática foi a teoria das séries de Fourier, podendo esta, então, ser considerada uma das teorias mais importantes da Análise.[5]
Embora o objetivo inicial de Joseph Fourier fosse resolver a equação do calor, depois que o método foi estudado e encontrado ele foi sendo usado para resolver muitos problemas matemáticos e físicos e, em especial, os que continham equações diferenciais. Esse estudo, conhecido hoje por Série de Fourier, tem aplicação direta nas áreas da engenharia elétrica, análise de vibrações, acústica, óptica, processamento de sinais, processamento de imagens, econometria.[7] De encontro com esse aspecto está que, durante a elaboração da Série de Fourier, Joseph Fourier não estava focado em entender o calor enquanto entidade física (explicitando que não era o foco dele, mas que na pressão de dar uma explicação ele diria que a condução do calor se daria como radiação) mas para ele o importante era descrever matematicamente o comportamento do calor.[8]
Funções ortogonais[editar | editar código-fonte]
Um conjunto ortogonal de funções é uma generalização de um conjunto ortogonal de vetores, seja um conjunto ortogonal de vetores um conjunto de vetores perpendiculares entre si. As propriedades de um conjunto ortogonal de funções são derivadas por analogia dos conjuntos ortogonais de vetores.[9]
Seja V ou um certo V(k) um vetor com n coordenadas definimos a fórmula que relaciona a norma do vetor com cada coordenada como:
.
Definição 1: A condição para que dois vetores sejam ortogonais é que o produto interno entre ambos seja igual a zero, e o produto interno é definido como:
Precisamos definir o que é um conjunto ortonormal de vetores, para isto usaremos primeiramente um conjunto de 3 vetores ortogonais. Seja um conjunto de 3 vetores, ou seja, teremos onde cada vetor possui 3 coordenadas. Calculamos as componentes de um vetor que faz parte do conjunto ortonormal de vetores segundo a fórmula:
em que n representa o vetor e k representa a sua respectiva coordenada. Note que o vetor é unitário e sua direção não mudou, portanto, neste exemplo, o conjunto ortonormal de vetores são os 3 que representam cada vetor .
Agora veja, podemos definir qualquer vetor, por exemplo , do espaço tridimensional como uma combinação linear do conjunto ortonormal, ou seja, o conjunto ortonormal forma uma base do espaço.[10] Portanto:
.
Podemos encontrar o coeficiente , basta usar as propriedades do produto interno:
seja , onde é o delta de Kronecker. Portanto:
.
Supondo agora que temos uma função contínua por partes onde representa a ordenada associada à abscissa k, se a função for definida para x dentro de um intervalo, agora não conseguimos mais obter a norma do vetor simplesmente usando a soma trivial, é natural pensar portanto que a soma do quadrado das componentes será feito por integração:
usando o mesmo princípio definimos o produto interno de duas funções como:
também podemos definir o conjunto . O conjunto ortonormal sobre o intervalo pode ser calculado da mesma forma que em vetores, como segue:
e o produto interno entre eles também, lembrando é claro que agora temos que cobrir todo o intervalo e não usamos mais soma e sim a integral dentro do intervalo:
.
A ideia agora é escrever a função f(x) como uma combinação linear do conjunto ortonormal de funções, ou seja,
lembrando que x precisa estar dentro do intervalo. Quando estávamos lidando com vetores podíamos descobrir os coeficientes da série, e com funções não será diferente, podemos usar a mesma ideia proposta quando estávamos trabalhando com vetores: obter o produto interno de ambos os lados envolvendo , obtendo desta forma o coeficiente através da definição de produto interno. Portanto:
(produto interno entre as funções)
Agora já estamos aptos a definir a série de Fourier generalizada através das funções ortogonais e do produto interno entre a função e o conjunto de funções ortogonais que define cada coeficiente da série:
.
Definição[editar | editar código-fonte]
Uma série trigonométrica é uma série da forma
Seja uma função periódica de período , ou seja para todo , a qual satisfaz às seguintes condições, conhecidas como as condições de Dirichlet:
- A função é unívoca/injetora (de um para um), e contínua exceto em um número finito de descontinuidade ordinárias dentro do período 2L;
- A função tem um número finito de máximos e mínimos dentro do período 2L;
- A função é absolutamente integrável, ou seja, a integral converge;
Então define-se a Série de Fourier da função como a série trigonométrica dada pelos coeficientes:
,
,
para n inteiro. Observamos aqui que, como periódica de período , o intervalo de integração pode ser qualquer intervalo de comprimento , sendo que geralmente são utilizados ou .[6]
Os coeficientes , e , são conhecidos como coeficientes de Fourier.
Forma Harmônica[editar | editar código-fonte]
Também podemos expressar a série de Fourier da função com período como[11]
em que
- , para
A igualdade entre a forma harmônica e a forma trigonométrica se dá por meio da identidade trigonométrica do cosseno da diferença:
Aplicando a identidade na forma harmônica, tem-se que:
Comparando os termos com os da representação trigonométrica, tem-se que:
- e
Forma complexa[editar | editar código-fonte]
Usando-se as expressões para as funções trigonométricas provenientes da fórmula de Euler:
Substituindo-as na forma harmônica da série de Fourier:
em que
Considerando a paridade das funções cosseno (par) e seno (ímpar) é possível notar que
e
em que foi usado
e
Como notação é tomado: , tal que dado por
Para calcular os coeficientes com índices diferentes de zero utilizamos a fórmula de Euler:
Logo,
Para a expressão da função obtemos
que pode ser simplificada em
Exemplos[editar | editar código-fonte]
| Domínio do tempo
|
Gráfico | Domínio da Frequência
|
Observações | Referência |
|---|---|---|---|---|
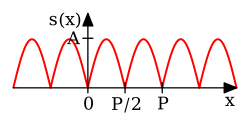 |
Onda completa retificada (seno) | [12]:p. 193 | ||
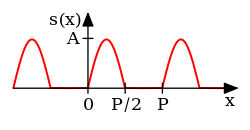 |
Meia onda retificada (seno) | [12]:p. 193 | ||
 |
||||
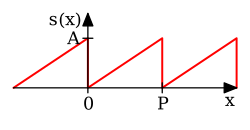 |
[12]:p. 192 | |||
 |
[12]:p. 192 | |||
 |
[12]:p. 193 |
Para a função -periódica dada por
encontramos os seguintes coeficientes de Fourier[13][14]
,
Logo, a série de Fourier de é dada por
A função onda quadrada escrita na forma trigonométrica da Série de Fourier é dada por:
com
Encontrando os seguintes coeficientes: e
A função onda quadrada pode ser escrita na forma exponencial como
Diagramas de espectro[editar | editar código-fonte]
Os coeficientes da expansão de uma função em Série de Fourier Complexa são números complexos. É comum representar os na forma de módulo e fase, isto é:
Pode-se representar através de dois diagramas: um para as suas amplitudes (conhecido como espectro de amplitudes) e outro para as suas fases (conhecido como espectro de fases):[15]
• Espectro de amplitudes: é um diagrama onde grafa-se os valores das amplitudes dos coeficientes de Fourier versus , isto é, um gráfico da forma: × .
• Espectro de fase: é um diagrama onde grafa-se os valores das fases dos coeficientes de Fourier versus , isto é, um gráfico da forma: × .
Convergência[editar | editar código-fonte]
Nas aplicações da engenharia, normalmente se presume que a Série de Fourier converge em todos os pontos, exceto nas descontinuidades. Isso se deve ao fato de que essas funções são mais comportadas do que as que os matemáticos fornecem em contrapartida. Em particular, se é contínua e derivada de , que pode apresentar descontinuidade, é integrável ao quadrado, então a Série de Fourier converge para . Se uma função é integrável ao quadrado no intervalo , então a série de Fourier converge para a função em praticamente todos os pontos. A convergência das séries de Fourier também depende do número finito de máximos e mínimos em uma função que é popularmente conhecida como uma das condições de Dirichlet para as séries de Fourier. É possível definir coeficientes de Fourier para funções ou distribuições mais gerais, nesses casos a convergência em norma ou convergência fraca é usualmente de interesse.[16]
Propriedades[editar | editar código-fonte]
Teorema de Parseval[editar | editar código-fonte]
Considerando uma função , com período e representável por uma série de Fourier, a seguinte identidade é válida:
Sendo os coeficientes complexos da série analisada.
Esta integral se relaciona com o conceito de potência média de um sinal.
Demonstração do Teorema de Parseval[17][editar | editar código-fonte]
Considerando que
Como , temos
Substituindo esta expressão para na definição de Potência Média dada por
temos,
Como ,temos:
Funções pares e ímpares[editar | editar código-fonte]
As séries de Fourier transparecem em seus coeficientes a paridade das funções:[14]
- Se f(t) for uma função ímpar, e para todo e, além disso para .
- Se f(t) for uma função par, para todo e, além disso, para
Algumas considerações sobre essas funções são importantes:
- A soma e a diferença de duas funções pares é par;
- A soma e a diferença de duas funções ímpares é ímpar;
- A soma e a diferença de uma função par e uma função ímpar não é nem par nem ímpar;
- O produto e o quociente de duas funções pares é par;
- O produto e o quociente de duas funções ímpares é par;
- O produto e o quociente de uma função par e uma função ímpar é ímpar.
Essas afirmações são úteis para o estudo da Transformada de Fourier, pois auxiliam no processo de integração.[18]
Fenômeno de Gibbs[editar | editar código-fonte]
A convergência das somas parciais de séries de Fourier de funções suaves por partes em torno de um salto, encontra-se oscilações cujas amplitudes não convergem para zero. Tal fenômeno envolve o fato que mesmo com a adição de mais termos a soma parcial, a ultrapassagem nos saltos das descontinuidades não desaparece. Temos a convergência ponto a ponto, no entanto, ao avaliarmos a diferença entre a função e a soma parcial, sempre encontramos um ponto onde esse valor é aproximadamente 8,9% da amplitude do salto.[19]
Aplicações[editar | editar código-fonte]
As séries de Fourier são capazes de representar uma família de funções periódicas envolvendo tanto funções contínuas como não contínuas, diferentemente das séries de Taylor, que só representam funções contínuas e deriváveis[20]. Algumas das funções representáveis podem ter significado físico, como os sinais musicais ou elétricos. Essas séries também são amplamente utilizadas na resolução de equações diferenciais parciais, como a equação da onda, do calor e problemas envolvendo a Equação de Laplace.
Para funções não periódicas a série de Fourier não está definida. Faz-se, então, o uso da transformada de Fourier, que possui uma possibilidade de aplicação mais ampla.
O uso da série nos sistemas de compressão como MP3, JPG, AVI, mantendo os sons e imagens com boa qualidade, ocupando apenas uma fração do espaço de armazenamento ou meio de transmissão que seus originais sem perdas necessitam.[4] Em outras palavras, a série tornou imagens e músicas digitais em coisas práticas e, com rápido compartilhamento.[4]
Usando as ferramentas e técnicas da espectroscopia por exemplo, astrônomos deduzem a composição química de uma estrela pela análise das componentes frequenciais (espectro) a partir das luzes emitidas pela estrela; engenheiros otimizam o projeto de um sistema de telecomunicações usando informações sobre as componentes espectrais de um sinal de dados que um sistema transportará.[21]
Na medicina e biologia, em estudos de morfologia dentofacial, a aplicação de funções de Fourier para comparar a forma da arcada dentária, os perfis faciais e a forma mandibular entre diferentes populações humanas e gêmeos, forneceu novas informações sobre influências genéticas e ambientais na variação destas estruturas. Diferenças no tamanho e forma dos arcos dentários entre diferentes populações humanas forneceram evidências indiretas das diferenças genéticas subjacentes entre os grupos. Enquanto os aborígines australianos tendiam a ter maior arcada dentária maxilar e mandibular do que japoneses ou caucasianos, as diferenças mais significativas eram aspectos da forma do arco. os caucasianos e os japoneses exibiram arcos maxilares e mandibulares mais afunilados do que os australianos. Além disso, comparações de amplitudes de Fourier descrevendo arcos dentários em gêmeos forneceram evidências da influência de fatores genéticos no tamanho do arco e na relação entre a profundidade / largura do arco.[22]
Sinais Discretos[editar | editar código-fonte]
Vamos considerar que o espectro da função é composto apenas por frequências inferiores a , onde é chamado de frequência de corte. Mostraremos que se conhecermos apenas os valores de para , k ∈ Z, onde T é o período de amostragem e é a frequência de amostragem, então podemos reconstruir exatamente em todos instantes de tempo. Considere uma função real, definiremos uma versão discretizada deste sinal da seguinte forma:
Assim é um trem de Dirac’s cujas amplitudes coincidem com o valor da função nos pontos de amostragem .
A fim de calcularmos a transforma de Fourier de , observamos que:
onde é uma função periódica cuja série de Fourier é dada por:
e assim,
e, portanto:
e finalmente:
onde se usou a propriedade do deslocamento no eixo .


Observamos que se a frequência de amostragem for superior a , então no intervalo e, portanto, toda a informação de é preservada. De fato, neste caso, podemos escrever:
Como pode ser calculada apenas com base nos pontos de amostragem, pode ser reconstruída. Se , então existe superposição espectral, o que impede a reconstrução da . Este resultado é conhecido como teorema da amostragem de Nyquist-Shannon ou teorema cardinal da interpolação.
Passagem do discreto para o contínuo[23][editar | editar código-fonte]
Suponhamos uma função não periódica. Definimos:
Onde:
- é uma função não periódica;
- é uma função T-periódica que coincide com no intervalo citado.
Dessa forma, é possível representar a função em Série de Fourier, pois a função carrega informação sobre a .
Exemplificando, temos a função não periódica :
- Queremos aproximar o máximo de , ou seja, obter o limite quando ;
- representa o período da função , dessa forma quando cresce a frequência fundamental decresce.
Assim, a função possui Série de Fourier da forma:
Cujo é possível calcular sabendo que
Como quando cresce a frequência fundamental decresce num gráfico as raias ficam cada vez mais próximas num diagrama de espectro, ou seja, é possível observar um aumento da densidade das linhas espectrais, e podemos escrever como:
Agora, podemos definir:
E também em termos de :
Que fazendo o limite de a soma de Riemann converge para a integral , onde
Aplicações na Matemática[editar | editar código-fonte]
A Série de Fourier é utilizada na área de Matemática Aplicada, sendo amplamente utilizada na transformada de Fourier. Essa transformada é de extrema importância, pois é capaz de diminuir, por exemplo, a quantidade de informações que precisamos guardar para recriar uma onda. Desse modo, conseguimos recriar a onda apenas guardando as frequências que a compõem, em vez de armazenar cada ponto da amplitude dessa onda. Como essa transformada é de suma importância, discutiremos sobre algumas propriedades importantes dessa transformada:
Linearidade[editar | editar código-fonte]
Uma das mais importantes propriedades da transformada de Fourier é a linearidade.
- Demonstração da Linearidade:
Considere que:
Assim,
utilizando a definição acima, temos que: sendo X(w) e Y(w) as transformadas de Fourier. [18]
Transformada da Derivada[editar | editar código-fonte]
Se f(t) é uma função diferenciável, sua transformada de Fourier é
utilizando a integração por partes temos:
então [19]
Transformada da integral[13][editar | editar código-fonte]
Dada uma função integrável , na qual sua transformada de Fourier satisfaça , e considerando uma e o teorema fundamental do cálculo em que , podemos ver que:
É observável que:
e assim
Chegando, dessa forma, à propriedade em si:
Simetria ou Dualidade[editar | editar código-fonte]
Considerando uma função f(t), temos
pela definição de Fourier , calculamos então a f(w), para isso trocamos t e w
Então, podemos afirmar que
Essas são algumas das propriedades que auxiliam no cálculo da Transformada de Fourier[17]
Inversão temporal[13][editar | editar código-fonte]
Uma propriedade muito importante que é muito visível no cotidiano é a propriedade da inversão temporal, a qual demonstra os efeitos de quando ouvimos a música de trás para frente, por exemplo. Ao considerarmos uma e uma , temos que:
Ao considerarmos a mudança de variável , temos que:
E assim, temos a propriedade, em que
Deslocamento na frequência [24][editar | editar código-fonte]
Dada uma função f(t) e sua transformada de Fourier F() , então
Demonstração:
Deslocamento no tempo [24][editar | editar código-fonte]
Dada uma função f(t) e sua transformada de Fourier F() , então
Demonstração
Conjugação [24][editar | editar código-fonte]
Dada uma função real f(t) e sua transformada de Fourier , então
Demonstração
Modulação[editar | editar código-fonte]
Dada uma função f(t) e sua transformada de Fourier , então:
Para a função cosseno é factível que a proposição é válida porque:
No que se refere à função seno, pode-se provar o teorema por meio da seguinte demonstração:
Mudança de Escala[editar | editar código-fonte]
Dada uma função f(t) e sua transformada de Fourier , então
Demonstração:
Da definição de transformada de Fourier, temos
Fazendo a mudança , distinguindo dois casos:a0 e a0.
Para = a0 temos:
Para o caso a0, temos:
Em ambos os casos, temos:
Aplicações em Acústica e Sons[editar | editar código-fonte]
Chamamos de som toda e qualquer vibração das moléculas de ar que estão imediatamente próximas de nossos tímpanos. Ao fazê-lo, tais vibrações são captadas pela membrana sensível do órgão e assimiladas pelos sensores nervoso da orelha interna, resultando na sensação de escuta em nosso cérebro. No entanto, sinais sonoros podem ser de vários tipos, desde ruídos bruscos e desagradáveis até belos acordes de um instrumento musical.
Podemos explicar a natureza sonora utilizando a teoria de Séries de Fourier e enxergando uma excitação sonora que atinge nossos ouvidos como um sinal periódico em função do tempo, com o formato de uma onda senoide muito complexa, isto é, de desenho bifurcado, repleta de amplitudes diferentes em cada ponto. Esta onda, por sua vez, nada mais é que é uma soma de inúmeras ondas senoidais simples, cada uma ponderada com sua própria amplitude (coeficientes de Fourier) e oscilando à sua própria frequência (harmônicos). Em uma expansão em Séries de Fourier, harmônicos em termos subsequentes são especialmente ordenados, de tal forma que todos acabam sendo múltiplos de um primeiro mais baixo e dominante na nossa percepção do som, o qual denotamos Frequência Fundamental . Logo, as próximas devem obedecer um relação , onde cresce conforme aumentam os harmônicos.
É aqui que reside a explicação para distinção de diferentes tipos de som[25], advindos de diferentes instrumentos musicais por exemplo. Instrumentos de percussão como tambores geralmente possuem expansão em Série de Fourier mais simples e com poucos termos, soando somente os primeiros harmônicos mais graves e mais ressaltados, o que resulta no som seco e rústico de uma batida de tambor. Já um violino produzirá muitas de suas vibrações em frequências mais altas, pois são estas que dão riqueza ao som, caracterizando os sons mais bonitos e elaborados do instrumento. É também por trabalhar em harmônicos altos que identificamos o som de um violino como mais fino ou agudo.[26]
Assim, se decompormos um sinal sonoro em Série de Fourier e tocarmos apenas o primeiro termo de seno ou cosseno (nosso ouvido não é capaz de perceber a defasagem entre os dois) da série, escutaremos um som seco, grave e desagradável. À medida que adicionamos os termos subsequentes, vamos refinando este som e aos poucos tornando-o mais agradável, assimilando novas camadas sonoras vindas das novas frequências. Chamamos de timbre a singularidade que esse fenômeno dá à cada som, isto é, a capacidade de discernir entre fontes graças às ondas diferentes que decompõem o sinal resultante.
Uma nota é composta por um conjunto de frequências que são dobras umas das outras, ou seja, diferentes escalas, mas divididas em intervalos iguais de razão , os quais chamamos de oitavas. Digamos, por exemplo, que tocamos a nota Dó em um piano, chamando de sua frequência. Ao tocarmos uma frequência , estaríamos produzindo novamente um Dó, uma oitava mais agudo. Em , surge mais um Dó, desta vez duas oitavas mais agudo. O mesmo ocorre para outras frequências presentes no espectro. , por exemplo, representaria uma nota diferente, sendo esta mesma nota porém na próxima escala[27]. Uma ferramenta poderosa e importante para este tipo estudo é construir diagramas de espectro para cada sinal. Deste modo é possível visualizar seu comportamento no domínio-frequência e identificar facilmente sob quais harmônicos este está trabalhando.
Aplicações na Engenharia Hídrica[editar | editar código-fonte]
Conforme Ricieri(1988)[28], embora a série de Fourier tenha sido desenvolvida como subsídio matemático ao estudo da transferência de calor, a aplicação dessa soma de senos e cossenos estendeu -se aos ramos da física , engenharia e matemática, sendo também comum encontrar o uso da série de Fourier em artigos que propõem modelos para análise da periodicidade de alguns eventos climáticos. Assim de um modo geral, pode-se dizer que a série desenvolvida por Fourier têm permitido que engenheiros e cientistas escrevam diversos tipos de funções e com elas podem administrar e prever cenários futuros nas mais diversas áreas de estudo.[29]
Logo, vários fenômenos e grandezas físicas presentes na atmosfera terrestre, por apresentarem um caráter quase periódico, podem ser descritos com uso de séries de Fourier, a exemplo das precipitações em suas variações sazonais, radiação que chega ao topo da atmosfera, padrões de vento, temperatura, umidade do ar, etc.[29]
Sendo a pluviosidade um elemento climático fundamental por ter influência direta nas demais variáveis que compõem o meio ambiente(temperatura do ar ,radiação solar, umidade atmosférica), é de suma importância no desenvolvimento da fauna e flora que compõem um ecossistema.[30]
Por possuírem caráter fundamental para um ecossistema, modelos são criados a partir de modelagem atmosférica relacionando a periodicidade de chuvas e pluviometria com o fator tempo. Esses modelos possuem propósito de encontrar padrões e prever cenários futuros através de séries de Fourier além prever eventos extremos.[30]
Outra utilização importante na análise de Fourier, foi o estudo proposto por William Thomson, que envolvia a análise e predição harmônica, para detectar o comportamento das marés ao longo do ano.
Série de Fourier em um quadrado[editar | editar código-fonte]
Artigo principal: Fourier Series
É possível definir a série de Fourier para funções de duas variáveis, como e , num intervalo
, onde
Além dessa definição ser útil para resolver equações diferenciais parciais, uma aplicação notável da série de Fourier no quadrado é a compressão de imagens. Em particular, o padrão de compressão de imagem jpeg usa a transformação cosseno discreta bidimensional, que é uma transformação de Fourier usando as funções básicas do cosseno.
Ver também[editar | editar código-fonte]
- Análise de Fourier
- Número de Fourier
- Lei de Fourier
- Equação do calor
- Equação da onda
- Equação de Laplace
- Transformada de Fourier
Referências
- ↑ a b c «Estude mais rápido e mande bem na prova». Responde Aí. Consultado em 20 de abril de 2018
- ↑ a b c Galdino, Pereira, André (9 de novembro de 2012). «Séries de Fourier e aplicações»
- ↑ a b c d e «As séries de Fourier». Série tintim por tintim. Seara da Ciência. Consultado em 20 de abril de 2018
- ↑ a b c d e «A música digital não existiria sem a transformada de Fourier - Gizmodo Brasil». Gizmodo. Portal Universo Online. Consultado em 20 de abril de 2018
- ↑ a b c d Revista Matemática Universitária n° 11, junho de 1990, p. 27-52.
- ↑ a b c Figueiredo, Djairo Guedes de (1977). Análise de Fourier e equações diferenciais parciais Terceira ed. Rio de Janeiro: IMPA. p. 16-18,40-42.
- ↑ Nerlove, Marc; Grether, David M.; Carvalho, José L. (1995). Analysis of Economic Time Series. Economic Theory, Econometrics, and Mathematical Economics. [S.l.]: Elsevier
- ↑ Pifer; Aurani, Anderson; Katya Margareth (30 de março de 2015). «A teoria analítica do calor de Joseph Fourier: uma análise das bases conceituais e epistemológicas». Revista Brasileira de Ensino de Física. Consultado em 23 de setembro de 2019
- ↑ Churchill, Ruel (1963). Fourier Series and Boundary Problems. [S.l.: s.n.]
- ↑ Boldrini, José (1980). Álgebra Linear. [S.l.: s.n.]
- ↑ Hsu, Hwei P. (1973). Análise de Fourier. Rio de Janeiro: Livros Técnicos e Científicos Ltda. p. 04,16,52-54.
- ↑ a b c d e Papula, Lothar (2009). Mathematische Formelsammlung: für Ingenieure und Naturwissenschaftler [Mathematical Functions for Engineers and Physicists] (em alemão). [S.l.]: Vieweg+Teubner Verlag. ISBN 3834807575
- ↑ a b c «Séries de Fourier e exemplos». REAMAT, Recursos Educacionais Abertos de Matemática. Instituto de Matemática e Estatística da Universidade Federal do Rio Grande do Sul. Consultado em 17 de julho de 2018
- ↑ a b Zill, Cullen, Dennis G., Michael R. (2001). Equações Diferenciais terceira ed. São Paulo: Pearson Makron Books. p. 213,215-216
- ↑ «matematica.pucminas.br». www.matematica.pucminas.br. Consultado em 17 de dezembro de 2020
- ↑ Tolstov, Georgi (1976). Fourier Series. [S.l.]: Courier-Dover
- ↑ a b Sauter, de Azevedo, Ezequia, Fábio (15 de maio de 2019). «Análise de Fourier, Um Livro Colaborativo» (PDF). Consultado em 20 de junho de 2019
- ↑ a b Valle, Marcos Eduardo. «Teoremas e Propriedades das Séries de Fourier.» (PDF). Consultado em 19 de junho de 2019
- ↑ a b AZEVEDO, Fábio; SAUTER, Esequia; STRAUCH, Irene (30/03/2016). Transformadas. http://www.mat.ufrgs.br/~aplicada/Notas_Transformadas.pdf
- ↑ Anton, Howard (2000). Cálculo, um novo horizonte sexta ed. Porto Alegre: Bookman. p. 69-77
- ↑ «admin, Gestor/a de la revista, Aula Palma 12-6.pdf». dx.doi.org. Consultado em 5 de julho de 2019
- ↑ Lestrel, Pete E. (13 de maio de 1997). Fourier Descriptors and Their Applications in Biology (em inglês). [S.l.]: Cambridge University Press. ISBN 9780521452014
- ↑ Sauter, Souto de Azevedo, Esequia, Fábio (15 de maio de 2019). «Passagem do discreto para o contínuo». www.ufrgs.br. Universidade Federal do Rio Grande do Sul. Consultado em 29 de novembro de 2019
- ↑ a b c «Propriedades». www.ufrgs.br. Consultado em 5 de julho de 2019
- ↑ Jessop, Shunteal (2017). «The Historical Connection of Fourier Analysis to Music». The Mathematics Enthusiast. Consultado em 3 de julho de 2019 line feed character character in
|titulo=at position 49 (ajuda) - ↑ Visintin (2016). «Fourier Series and Musical Theory» (PDF). Consultado em 3 de julho de 2019
- ↑ Brietzke, Eduardo (14 de dezembro de 2001). «Séries de Fourier e Noções de Teoria Musical». Universidade Federal do Rio Grande do
Sul. Consultado em 3 de julho de 2019 line feed character character in
|publicado=at position 39 (ajuda) - ↑ RICIERI, Aguinaldo Prandini (1988). RICIERI, A. P. (1988). Construindo a Série de Fourier. São Paulo: Prandiano. São Paulo: Prandiano
- ↑ a b Duarte, Joelma Vieira do Nascimento. "Caracterização do regime pluvial do semiárido paraibano utilizando série de Fourier." (2017).
- ↑ a b «Fatores e elementos climáticos. Principais elementos climáticos - Brasil Escola». Brasil Escola. Consultado em 20 de novembro de 2018

![{\displaystyle T(t)={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\left[a_{n}\cdot \cos \left({\frac {n\pi t}{L}}\right)+b_{n}\cdot \operatorname {sen} \left({\frac {n\pi t}{L}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82f8de611de90667381185e03a4bc0efd54922e6)


































![{\displaystyle [0,2L]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/375d91caea37b8b2615fb8b15cbf3a11b9904e75)
![{\displaystyle [-L,L]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3821e4ce807a6a5d059c66d3c8802a17a8d6e92c)









![{\displaystyle f(t)=A_{0}+\sum _{n=1}^{\infty }[A_{n}\cos(\theta _{n})\cos(w_{n}t)+A_{n}\sin(\theta _{n})\sin(w_{n}t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50376fafa32c25370dfec98d3cbc840af0aa439e)





![{\displaystyle f(t)={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\left[a_{n}{\frac {e^{iw_{n}t}+e^{-iw_{n}t}}{2}}-ib_{n}{\frac {e^{iw_{n}t}-e^{-iw_{n}t}}{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09df06f9aa471b91d56b8b3bcebeb149acbed011)

![{\displaystyle f(t)={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\left[{\frac {a_{n}-ib_{n}}{2}}e^{iw_{n}t}+{\frac {a_{n}+ib_{n}}{2}}e^{-iw_{n}t}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9c1f64858b4a7b945429e7032a90583c53b5926)












































![{\displaystyle [xo,xo+T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2586bd2dacd70a3f2e4402348bbc988ef71a9e84)






![{\displaystyle {\frac {1}{T}}\int _{0}^{T}|f(t)|^{2}dt={\frac {1}{T}}\int _{0}^{T}f(t){\overline {f(t)}}\,dt={\frac {1}{T}}\int _{0}^{T}f(t){\Bigl [}{\sum _{n=-\infty }^{\infty }{\overline {C_{n}}}e^{-iw_{n}t}}{\Bigr ]}dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/685b50513a800c6233aec7cfbdd07c2d93e97c36)
![{\displaystyle {\frac {1}{T}}\int _{0}^{T}|f(t)|^{2}dt={\frac {1}{T}}{\sum _{n=-\infty }^{\infty }{\Bigl [}{\overline {C_{n}}}\int _{0}^{T}f(t)e^{-iw_{n}t}}dt{\Bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64953330f10c3782b0e8ebdac24bd5e0b861ecc6)

























![{\displaystyle [-w_{c},w_{c}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7152b292488c01bff07ffab30978e832ff65370)


















![{\displaystyle {\mathcal {F}}\{ax(t)+by(t)\}=\int \limits _{-\infty }^{\infty }[ax(t)+by(t)]e^{-itw}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40e8e7037f3b484d058b24e873a27de2e47b4759)

![{\displaystyle F[ax(t)+by(t)]=aX(w)+bY(w)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b3a9eeebd512b2423bf3cfadf4902ffc3694288)













































![{\displaystyle {\begin{aligned}{\mathcal {F}}\{f(t)sen(w_{0}t)\}&=\int _{-\infty }^{\infty }f(t){\biggl (}{\frac {e^{iw_{0}t}-e^{-iw_{0}t}}{2i}}{\biggr )}e^{-iwt}dt\\{\mathcal {F}}\{f(t)sen(w_{0}t)\}&={\frac {1}{2i}}{\biggl [}\int _{-\infty }^{\infty }f(t)e^{i(w-w_{0})t}dt-\int _{-\infty }^{\infty }f(t)e^{i(w+w_{0})t}dt{\biggr ]}\\{\mathcal {F}}\{f(t)sen(w_{0}t)\}&={\frac {1}{2i}}{\biggl [}F(w-w_{0})-F(w+w_{0}){\biggr ]}\\{\mathcal {F}}\{f(t)sen(w_{0}t)\}&={\frac {F(w-w_{0})}{2i}}-{\frac {F(w+w_{0})}{2i}}\\{\mathcal {F}}\{f(t)sen(w_{0}t)\}&=-{\frac {i}{2}}F(w-w_{0})+{\frac {i}{2}}F(w+w_{0})\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74322fc430834ce4d4bf0d261ccb93e9d0f6156b)






















![{\displaystyle [-\pi ,\pi ]\times [-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df436805f50de7386abdb2a9d058672ec1b4cebb)


