Integral

 Nota: Se procura o telescópio espacial INTErnational Gamma-Ray Astrophysics Laboratory (INTEGRAL), veja INTEGRAL.

Tópicos em cálculo

Teorema fundamental Limites de funções Continuidade Cálculo vetorial Cálculo matricial Teorema do valor médio Derivação  Regra do produto Regra do quociente Regra da cadeia Mudança de variáveis Diferenciação implícita Teorema de Taylor Taxas relacionadas Tabela de derivadas Integração  Tábua de integrais Integral imprópria Integração por: partes, substituição, substituição trigonométrica, frações parciais Cálculo vetorial Gradiente Divergência Rotacional Laplaciano Teorema do gradiente Teorema de Green Teorema de Stokes Teorema da divergência Cálculo de várias variáveis  Cálculo matricial Derivada parcial Integral Múltipla Integral de linha Integral de Superfície Integral de volume Matriz jacobiana

No cálculo, a integral de uma função foi criada originalmente para determinar a área sob uma curva no plano cartesiano e também surge naturalmente em dezenas de problemas de Física, como por exemplo na determinação da posição em todos os instantes de um objeto, se for conhecida a sua velocidade instantânea em todos os instantes. ^{[carece de fontes]}

O processo de se calcular a integral de uma função é chamado de integração.

Diferentemente da noção associada de derivação, existem várias definições para a integração, todas elas visando a resolver alguns problemas conceituais relacionados a limites, continuidade e existência de certos processos utilizados na definição. Estas definições diferem porque existem funções que podem ser integradas segundo alguma definição, mas não podem segundo outra.

A integral também é conhecida como antiderivada.

Definição formal e notação

Integral definida

Integrando a área de uma função abaixo de uma curva

Seja f uma função contínua definida no intervalo [a,b]. A integral definida desta função é denotada como:

Em linguagem matemática	Em Português
$S = {\int_{a}^{b}} {f(x)} dx$	S é a integral da função f(x), no intervalo entre a e b. ${\int}$ é o sinal da integral, f(x) é o integrando e os pontos a e b são os limites (inferior e superior, respectivamente) de integração.
Onde ${f}: \left [ {a},{b} \right ] \rightarrow \mathbb{R}$	f é uma função com domínio no espaço fechado [a,b] (com ${a} \le x \le {b}$) e com imagem no conjunto dos números reais

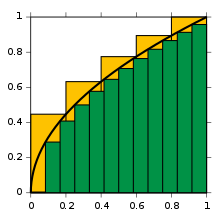
A ideia desta notação utilizando um S comprido é generalizar a noção de somatório. Isto porque intuitivamente a integral de f(x) pode ser entendida como a soma de pequenos retângulos de base Δx tendendo a zero e altura ${f(x_i^*)}$, onde o produto $\Delta x {f(x_i^*)}$ é a área deste retângulo. A soma de todas estas pequenas áreas, ou áreas infinitesimais, fornece a área total abaixo da curva. Mais precisamente, pode-se dizer que a integral acima é o valor limite da soma:

Em linguagem matemática	Em Português
${\int_{a}^{b}} {f(x)} dx = \lim_{n\to\infty} \sum_{i=1}^{n} {f(x_i^*)} \Delta x$	A integral de f(x) no intervalo [a,b] é igual ao limite do somátório de cada um dos valores que a função f(x) assume, de 0 a n, multiplicados por Δx. O que se espera é que quando n for muito grande o valor da soma acima se aproxime do valor da área abaixo da curva e, portanto, da integral de f(x) no intervalo. Ou seja, que o limite esteja definido. A definição de integral aqui apresentada é chamada de soma de Riemann, mas há outras formas (equivalentes).
onde $\Delta x = \frac{b-a}{n}$	comprimento dos pequenos subintervalos nos quais se divide o intervalo [a,b]. Os extremos destes intervalos são os números $x_0 \left ( =a \right ),x_1,...x_n \left ( =b \right )$.
onde ${f(x_i^*)}$	Valor ("altura") da função f(x) quando x é igual ao ponto amostral $x_i^*$, definido como um ponto que está no subintervalo $\left [ x_{i-1},x_i \right ]$ (podendo até mesmo ser um destes pontos extremos do subintervalo).

Uma integral definida pode ser própria ou imprópria, convergente ou divergente. Neste último caso, ela representa uma área infinita.

Integral indefinida

Integral indefinida é uma função (ou família de funções), assim definida :

$\int {f(x)}dx = F(x)$ se e somente se ${\frac{dF(x)}{dx}}= {f(x)}$, ou, o que é a mesma coisa, $\int {f(x)}dx = F(x) \leftrightarrow {F' \left ( x \right )} = {f(x)}$

Relação entre integral definida indefinida

A integral definida ${\int_{a}^{b}} {f(x)} dx$ é um número; não depende da variável x. A integral indefinida, ao contrário, é uma função ou família de funções. A conexão entre elas é dada pelo Teorema Fundamental do Cálculo. Se f for contínua em [a,b], então .

${\int_{a}^{b}} {f(x)} dx = \int {f(x)} dx |_a^b$

Ou seja, a integral indefinida, calculada no intervalo [a,b], resulta no valor da integral definida.

Teorema fundamental do Cálculo

Caso se resolva a integral acima entre os limites a e b, o resultado final pode ser escrito como:

$S = \int_{a}^{b} f(x) dx = F(b) - F(a)$

onde a função F(x) é a função resultante da integração da função f(x). O problema da integração, isto é, de se encontrar a solução para uma integral, se resume portanto a encontrar a função F(x).

O resultado acima é extremamente importante pois ele oferece uma indicação de como obter a integral. Para ver isto, supõe-se que o limite superior da integral, isto é, b, seja muito próximo de a, tal que se possa escrever:

b = a + Δx

Como os pontos limites da integral estão muito próximos, pode-se escrever:

$\int_{a}^{a+\Delta x} f(x) dx = F(a + \Delta x) - F(a)$

Olhando na definição da integração como um limite, dada acima, pode-se dizer que a integral, neste caso, se resume a apenas um dos termos na soma, e portanto pode-se afirmar, sem causar um erro muito grande, que:

$\int_{a}^{a+\Delta x} f(x) dx = f(a) \Delta x = F(a + \Delta x) - F(a)$

Comparando com a definição da derivada de uma função:

$f(x) = \frac{ F(x + \Delta x) - F(x) }{ \Delta x } \rightarrow f(x) = \frac{d}{dx} F(x)$

vê-se que a função procurada F(x) é uma função tal que, quando tomada a sua derivada, obtém-se a função f(x). Em outras palavras, ao se calcular a derivada de uma função pode-se também calcular a integral da função resultante. Esta propriedade mostra que a integração na verdade é a operação inversa da derivação, pois se uma função for derivada e em seguida o resultado integrado, obtém-se a função original. Esta propriedade é chamada de Teorema fundamental do Cálculo.

Passo-a-Passo

Integral Definida - Uma integral definida consta basicamente em integrar uma função constante nos intervalos, através das primitivas, que nada mais são do que a função integrada a cada membro.

Fórmula das Primitivas

$\int a\cdot x^{n} dx = \frac{a\cdot x^{n+1}} {n+1}$

Exemplo:

Cada membro da função é tratado como uma função em separado, para em seguida ser efetuada a soma entre eles e gerar outra função, a função na qual se substitui o valor de X pelos valores do intervalo. Feito isso, usa-se o teorema do cálculo para chegar ao valor da integral.

No intervalo (0,3)

f(x) = x² + 2x + 4

$\int x^{2} dx + \int (2x) dx + \int (4) dx$

Aqui usa-se a Fórmula da Primitiva em cada integral.

$\frac{x^{2+1}} {2+1} + \frac{2\cdot x^{1+1}} {1+1} + \frac{4 \cdot x^{0+1}} {0+1}$

Gera-se a outra função, que será usada para substituir os valores do intervalo.

$\frac{x^3} {3} + x^2 + 4\cdot x$

Para x = 0

f(a) = 0

Para x = 3

$\frac{3^3} {3} + 3^2 + 4\cdot 3$

f(b) = 30

Aplicação do teorema fundamental do Cálculo

Aproximações da integral de √x de 0 a 1, com ■ 5 amostras à direita (acima) e ■ 12 amostras à esquerda (abaixo)

$\int_{a}^{b} \frac {d}{dx}f(x) dx = f(b) - f(a)$

$\int_{0}^{3} (x^2+2x+4) dx = \frac{3^3} {3} + \frac{2.3^{2}} {2} + 4.3 - 0 = 3^2 + 3^2 + 12 = 9 + 9 + 12$

$\int_{0}^{3} (x^2+2x+4) dx = 30$

Exemplos de integração

Estas são as integrais de algumas das funções mais comuns:

$\int_{a}^{b} 1 dx = x|_a^b = (b-a)$ (Integral da função constante)

$\int_{a}^{b} x dx = \frac{1}{2} x^2|_a^b = \frac{1}{2}(b^2-a^2)$ (Integral da função f(x) = x )

Por definição a barra $f(x) |_a^b$ é utilizada com o significado da diferença f(b) − f(a)

Definições de integral

Para definições do processo de integração mais rigorosas veja os links abaixo

• Soma de Riemann
• Integral de Riemann
• Integral de Lebesgue
• Integral de Riemann-Stieltjes
• Integral de Henstock–Kurzweil ou integral de Gauge

Ver também

• Derivada
• Tábua de integrais
• Primitiva
• Integração numérica
• Métodos de integração
• Integral múltipla

Referências

• STEWART, James. Cálculo - volume I. São Paulo: Pioneira Thompson Learning, 2002. 4ª edição. ISBN 85-221-0235-X.