Derivada parcial

Cálculo
Teorema fundamental Limite de funções Continuidade Teorema do valor médio Teorema de Rolle
Cálculo Definições Derivada Diferencial Diferencial de uma função Generalizações da derivada Conceitos Notações para diferenciação Segunda derivada Terceira derivada Mudança de variáveis Derivação implícita Taxas relativas Teorema de Taylor Tabela de derivadas Somas Produto Regra da cadeia Potências Quocientes Fórmula de Faà di Bruno
Cálculo integral Tábua de integrais Definições Primitiva Integral Integral imprópria Integral de Riemann Integral de Lebesgue Integral de linha Integração por partes discos cascas cilíndricas substituição substituição trigonométrica Frações parciais mudança de ordem fórmulas de redução
Série Geométrica Aritmético-geométrica Harmônica Alternada Potências Binomial Taylor Laurent Fourier Testes de convergência Teste da divergência Razão Raiz Integral Comparação direta Comparação no limite Série alternada Condensação de Cauchy Dirichlet Abel
Cálculo vetorial Gradiente Divergência Rotacional Laplaciano Teorema do gradiente Teorema de Green Teorema de Stokes Teorema da divergência Derivada direcional
Cálculo com múltiplas variáveis Formalismo Matriz Tensor Exterior Geométrico Definições Derivada parcial Integral múltipla Integral de linha Integral de superfície Integral de volume Matriz jacobiana
Cálculo especializado Cálculo de variações Fracional Malliavin Estocástico

Em matemática, uma derivada parcial de uma função de várias variáveis é a sua derivada com respeito a uma daquelas variáveis, com as outras variáveis mantidas constantes. Este conceito é útil no cálculo vectorial e geometria diferencial.

A derivada parcial de uma função em relação ao seu argumento $x_{i}$ é representada ${\frac {\partial f(x_{1},...,x_{n})}{\partial x_{i}}}$.

Introdução

Um gráfico z = x² + xy + y². Para a derivada parcial em (1, 1, 3) que deixa y constante, a linha tangente correspondente é paralela ao plano xz.

Uma pedaço do gráfico acima, em y= 1

Suponha-se que ƒ é uma função de mais de uma variável. Para obter-se uma instância,

$z=f(x,y)=\,\!x^{2}+xy+y^{2}.\,$

O gráfico desta função define uma superfície no espaço euclidiano. Para cada ponto sobre esta superfície, há um número infinito de linhas tangenciais. Diferenciação parcial é o ato de escolher uma dessas linhas e encontrar o seu declive. Normalmente, as linhas de maior interesse são aquelas que são paralelas ao plano xz, e aquelas que são paralelos ao plano yz(que resultam da exploração ou y ou x constante, respectivamente.)

Para determinar o declive da linha tangente à função de P (1, 1, 3) que é paralela ao plano xz, o y variável é tratado como constante. O gráfico e este plano são mostrados à direita. No gráfico abaixo, vemos a forma como a função se comporta y = 1.Ao encontrar a derivada da equação assumindo que y é uma constante, e o declive ƒ no ponto(x, y, z) é:

${\frac {\partial z}{\partial x}}=2x+y$

Então, em (1, 1, 3), por substituição, o declive é de 3. portanto

${\frac {\partial z}{\partial x}}=3$

no ponto. (1, 1, 3). Ou seja, a derivada parcial de z com relação a x em (1, 1, 3) é 3.

Derivação parcial com limites

A derivada parcial de uma função de n argumentos $(x_{1},...,x_{n})$ pode ser representada através de um limite como sendo

${\frac {\partial f}{\partial x_{i}}}(x_{1},\ldots ,x_{n})=\lim _{h\to 0}{\frac {f(x_{1},\ldots ,x_{i}+h,\ldots ,x_{n})-f(x_{1},\ldots ,x_{n})}{h}}.$

A função f pode ser reinterpretada como uma família de funções de uma variável indexada pelas outras variáveis​​:

Em outras palavras, a cada valor de x define uma função, denotada fx, que é uma função de uma variável . Isto é,

$f_{x}(y)=x^{2}+xy+y^{2}.\,$

Uma vez que o valor de x é escolhido, em seguida, f ( x, y) determina a função f_a que envia y para a ² + ay + y ²

$f_{a}(y)=a^{2}+ay+y^{2}.\,$

Nesta expressão, a é uma constante, e não uma variável, então f_a é uma função de uma única variável real, sendo y. Consequentemente, a definição da derivada para uma função de uma variável aplica-se:

$f_{a}'(y)=a+2y.\,$

O procedimento acima pode ser realizada por qualquer escolha de a. Organizando as derivadas juntas em uma função dá uma função que descreve a variação de f na direção de y:

${\frac {\partial f}{\partial y}}(x,y)=x+2y.\,$

Este é o derivado parcial de f em relação a y. Aqui ∂ é um d arredondado, chamado o símbolo derivado parcial. Para distingui-la da letra d, ∂ às vezes é pronunciado "del" ou "parcial" em vez de "dê".

Em geral, a derivada parcial de uma função f(x₁,...,x_n) na direção no ponto x_i (a₁, ..., a) é definida como sendo:

${\frac {\partial f}{\partial x_{i}}}(a_{1},\ldots ,a_{n})=\lim _{h\to 0}{\frac {f(a_{1},\ldots ,a_{i}+h,\ldots ,a_{n})-f(a_{1},\ldots ,a_{i},\dots ,a_{n})}{h}}.$

No diferença quociente acima, todas as variáveis, exceto x_i são mantidas fixas. Essa escolha de valores fixos determina uma função de uma variável $f_{a_{1},\ldots ,a_{i-1},a_{i+1},\ldots ,a_{n}}(x_{i})=f(a_{1},\ldots ,a_{i-1},x_{i},a_{i+1},\ldots ,a_{n})$, e, por definição,

${\frac {df_{a_{1},\ldots ,a_{i-1},a_{i+1},\ldots ,a_{n}}}{dx_{i}}}(a_{i})={\frac {\partial f}{\partial x_{i}}}(a_{1},\ldots ,a_{n}).$

Em outras palavras, as diferentes opções de a indica uma família de funções de uma variável, assim como no exemplo acima. Esta expressão também mostra que o cálculo das derivadas parciais se reduz ao cálculo de uma variável derivada.

Derivação parcial de função vetorial

Um exemplo importante de uma função de várias variáveis ​​é o caso de um campo escalar f(x₁,...x_n) em um domínio no espaço Euclidiano Rⁿ (e.g., on R² or R³). Neste caso f tem uma derivada parcial ∂f/∂x_j com relação a cada variável x_j. No ponto a, estas derivadas parciais definem o vector

$\nabla f(a)=\left({\frac {\partial f}{\partial x_{1}}}(a),\ldots ,{\frac {\partial f}{\partial x_{n}}}(a)\right).$

Este vector é denominado gradiente de f em a. Se f é diferenciável em todos os pontos de algum domínio, então o gradiente é uma função vetorial de valor ∇f que leva o ponto a para o vetor ∇f(a). Consequentemente, o gradiente produz um campo vetorial.

Um problema comum de notação é definir o operador nabla (∇) ,como se apresenta em três dimensões espaciais euclidianas R³ com vetores unitários $\mathbf {\hat {i}} ,\mathbf {\hat {j}} ,\mathbf {\hat {k}}$:

$\nabla ={\bigg [}{\frac {\partial }{\partial x}}{\bigg ]}\mathbf {\hat {i}} +{\bigg [}{\frac {\partial }{\partial y}}{\bigg ]}\mathbf {\hat {j}} +{\bigg [}{\frac {\partial }{\partial z}}{\bigg ]}\mathbf {\hat {k}}$

Ou, mais geralmente, para o espaço euclidiano de n- dimensões Rⁿ com coordenadas (x₁, x₂, x₃,...,x_n) e vetores unitários ($\mathbf {{\hat {e}}_{1}} ,\mathbf {{\hat {e}}_{2}} ,\mathbf {{\hat {e}}_{3}} ,\dots ,\mathbf {{\hat {e}}_{n}}$):

$\nabla =\sum _{j=1}^{n}{\bigg [}{\frac {\partial }{\partial x_{j}}}{\bigg ]}\mathbf {{\hat {e}}_{j}} ={\bigg [}{\frac {\partial }{\partial x_{1}}}{\bigg ]}\mathbf {{\hat {e}}_{1}} +{\bigg [}{\frac {\partial }{\partial x_{2}}}{\bigg ]}\mathbf {{\hat {e}}_{2}} +{\bigg [}{\frac {\partial }{\partial x_{3}}}{\bigg ]}\mathbf {{\hat {e}}_{3}} +\dots +{\bigg [}{\frac {\partial }{\partial x_{n}}}{\bigg ]}\mathbf {{\hat {e}}_{n}}$

Definição formal

Como derivadas comuns, a derivada parcial é definida como sendo um limite. Sendo U um conjunto aberto de Rⁿ e f : U → R uma função. A derivada parcial de f no ponto a = (a₁, ..., a_n) ∈ U com relação à i- a variável a_i é definida como

${\frac {\partial }{\partial a_{i}}}f(\mathbf {a} )=\lim _{h\rightarrow 0}{f(a_{1},\dots ,a_{i-1},a_{i}+h,a_{i+1},\dots ,a_{n})-f(a_{1},\dots ,a_{i},\dots ,a_{n}) \over h}$

Mesmo se todas as derivados parciais ∂f/∂a_i(a) existirem em um determinado ponto a, a função não necessita de ser contínua.

No entanto, se todos as derivadas parciais existirem numa vizinhança de a e são contínuas, então f é o total derivado em que a derivada da vizinhança total é contínua. Neste caso, diz-se que f é uma C¹ função.

Isto pode ser utilizado para generalizar funções vetoriais (f : U → R'^m) com cuidado usando um argumento componente a componente.

A derivada parcial ${\frac {\partial f}{\partial x}}$ pode ser vista como uma outra função definida em U e pode ser novamente parcialmente diferenciada.

Se todas as derivadas parciais de segunda ordem mistas são contínuas em um ponto (ou um conjunto), f é denominado C² função naquele ponto (ou no conjunto); neste caso, as derivadas parciais podem ser trocadas pelo Teorema de Clairaut-Schwarz:

${\frac {\partial ^{2}f}{\partial x_{i}\,\partial x_{j}}}={\frac {\partial ^{2}f}{\partial x_{j}\,\partial x_{i}}}.$

Exemplos

Volume de um cone

O volume de um cone depende da altura e raio

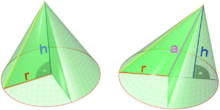
Considere-se o volume V de um cone; ele depende da altura do cone h e do seu raio r de acordo com a fórmula

$V={\frac {r^{2}h\pi }{3}}$

A derivada parcial de V com relação a r é

${\frac {\partial V}{\partial r}}={\frac {2rh\pi }{3}}$

e descreve a taxa com que o volume de um cone aumenta à medida que o seu raio também aumenta e a sua altura é mantida constante. A derivada parcial relativamente a h é

${\frac {\partial V}{\partial h}}={\frac {r^{2}\pi }{3}}$

Em contraste, a derivada total de V em relação à r e h são respectivamente

${\frac {\operatorname {d} V}{\operatorname {d} r}}=\overbrace {\frac {2\pi rh}{3}} ^{\frac {\partial V}{\partial r}}+\overbrace {\frac {\pi r^{2}}{3}} ^{\frac {\partial V}{\partial h}}{\frac {\operatorname {d} h}{\operatorname {d} r}}$

e

${\frac {\operatorname {d} V}{\operatorname {d} h}}=\overbrace {\frac {\pi r^{2}}{3}} ^{\frac {\partial V}{\partial h}}+\overbrace {\frac {2\pi rh}{3}} ^{\frac {\partial V}{\partial r}}{\frac {\operatorname {d} r}{\operatorname {d} h}}$

A diferença entre a derivada total e parcial é a eliminação de dependências indiretas entre as variáveis ​​nas derivadas parciais.

Se (por alguma razão arbitrária) proporções do cone têm de permanecer as mesmas, e a altura e raio estando em uma relação fixa k, temos

$k={\frac {h}{r}}={\frac {\operatorname {d} h}{\operatorname {d} r}}.$

Isto dá a derivada total no que se relaciona a r:

${\frac {\operatorname {d} V}{\operatorname {d} r}}={\frac {2\pi rh}{3}}+{\frac {\pi r^{2}}{3}}k$

Que simplifica para:

${\frac {\operatorname {d} V}{\operatorname {d} r}}=k\pi r^{2}$

Do mesmo modo, a derivada total no que refere a h é:

${\frac {\operatorname {d} V}{\operatorname {d} h}}=\pi r^{2}$

Equações envolvendo derivadas parciais de uma função desconhecida são chamadas de equação diferencial parcial e são comuns em física, engenharia e outras ciências e disciplinas aplicadas.

Otimização

As derivadas parciais aparecem em qualquer problema de otimização baseada em cálculos com mais de uma variável de escolha. Por exemplo, em economia, uma empresa pode desejar maximizar o lucro π(x, y) com relação à escolha das quantidades x e y de dois tipos diferentes de produção. As condições de primeira ordem para esta otimização são π_x = 0 = π_y. Como ambas as derivadas parciais π_x e π_y serão geralmente funções de ambos os argumentos x e y, estas duas condições de primeira ordem formam um sistema de duas equações em duas incógnitas.

Termodinâmica, mecânica quântica e física matemática

Derivados parciais aparecem em equações termodinâmicas como a Relação de Gibbs-Duhem, em mecânica quântica como a equação da onda de Schrodinger, assim como em outras equações da física matemática. Aqui as variáveis sendo mantidas constantes em derivadas parciais podem ser razão de variáveis simples como frações molares x_i no seguinte exemplo envolvendo as energias de Gibbs em um sistema de mistura ternária:

${\displaystyle {\bar {G_{2}}}=G+(1-x_{2})\left({\frac {\partial G}{\partial x_{2}}}\right)_{\frac {x_{1}}{x_{3}}}}$

Expressar as frações molares de um componente como funções da fração molar de outros componentes e rácios molares binários:

${\displaystyle x_{1}={\frac {1-x_{2}}{1+{\frac {x_{3}}{x_{1}}}}}}$

${\displaystyle x_{3}={\frac {1-x_{2}}{1+{\frac {x_{1}}{x_{3}}}}}}$

Os quocientes diferenciais podem ser formados em proporções constantes como os acima:

${\displaystyle \left({\frac {\partial x_{1}}{\partial x_{2}}}\right)_{\frac {x_{1}}{x_{3}}}=-{\frac {x_{1}}{1-x_{2}}}}$

${\displaystyle \left({\frac {\partial x_{3}}{\partial x_{2}}}\right)_{\frac {x_{1}}{x_{3}}}=-{\frac {x_{3}}{1-x_{2}}}}$

As proporções X, Y, Z das frações molares podem ser escritas para sistemas ternários e multicomponentes:

${\displaystyle X={\frac {x_{3}}{x_{1}+x_{3}}}}$

${\displaystyle Y={\frac {x_{3}}{x_{2}+x_{3}}}}$

${\displaystyle Z={\frac {x_{2}}{x_{1}+x_{2}}}}$

que pode ser usado para resolver equações diferenciais parciais como:

${\displaystyle \left({\frac {\partial \mu _{2}}{\partial n_{1}}}\right)_{n_{2},n_{3}}=\left({\frac {\partial \mu _{1}}{\partial n_{2}}}\right)_{n_{1},n_{3}}}$

Esta igualdade pode ser reordenada para ter um quociente diferencial de frações moles em um dos lados.

Redimensionamento de imagem

As derivadas parciais são a chave para algoritmos de redimensionamento de imagem com consciência de alvo. Amplamente conhecidos como escultura em costura, estes algoritmos exigem que cada pixel de uma imagem receba uma 'energia' numérica para descrever sua disparidade em relação aos pixels ortogonais adjacentes. O algoritmo então remove progressivamente as linhas ou colunas com a menor energia. A fórmula estabelecida para determinar a energia de um pixel (magnitude de gradiente em um pixel) depende muito das construções de derivadas parciais.

Economia

Os derivados parciais desempenham um papel proeminente na economia, na qual a maioria das funções que descrevem o comportamento econômico postula que o comportamento depende de mais de uma variável. Por exemplo, uma função de consumo social pode descrever o montante gasto em bens de consumo como dependendo tanto da renda quanto da riqueza; a propensão marginal ao consumo é então a derivada parcial da função de consumo com relação à renda.

Notação

Mais informações: ∂

Para os exemplos a seguir, deixe ${\displaystyle f}$ ser uma função em ${\displaystyle x,y}$ e ${\displaystyle z}$.

Derivadas parciais de primeira ordem:

${\displaystyle {\frac {\partial f}{\partial x}}=f_{x}=\partial _{x}f.}$

Derivadas parciais de segunda ordem:

${\displaystyle {\frac {\partial ^{2}f}{\partial x^{2}}}=f_{xx}=\partial _{xx}f=\partial _{x}^{2}f.}$

Derivadas mistas de segunda ordem:

${\displaystyle {\frac {\partial ^{2}f}{\partial y\,\partial x}}={\frac {\partial }{\partial y}}\left({\frac {\partial f}{\partial x}}\right)=(f_{x})_{y}=f_{xy}=\partial _{yx}f=\partial _{y}\partial _{x}f.}$

Derivadas parciais e mistas de ordem superior:

${\displaystyle {\frac {\partial ^{i+j+k}f}{\partial x^{i}\partial y^{j}\partial z^{k}}}=f^{(i,j,k)}=\partial _{x}^{i}\partial _{y}^{j}\partial _{z}^{k}f.}$

Ao lidar com funções de múltiplas variáveis, algumas destas variáveis podem estar relacionadas entre si, portanto pode ser necessário especificar explicitamente quais variáveis estão sendo mantidas constantes para evitar ambigüidade. Em campos como a mecânica estatística, a derivada parcial ${\displaystyle f}$ em relação a ${\displaystyle x}$ mantendo ${\displaystyle y}$ e ${\displaystyle z}$ contantes é freqüentemente expressa como ${\displaystyle \left({\frac {\partial f}{\partial x}}\right)_{y,z}.}$

Convencionalmente, para clareza e simplicidade da notação, a função derivada parcial e o valor da função em um ponto específico são conflacionados pela inclusão dos argumentos da função quando o símbolo da derivada parcial (notação Leibniz) é usado. Assim, uma expressão como

${\displaystyle {\frac {\partial f(x,y,z)}{\partial x}}}$

é usado para a função, enquanto

${\displaystyle {\frac {\partial f(u,v,w)}{\partial u}}}$

pode ser usado para o valor da função no ponto ${\displaystyle (x,y,z)=(u,v,w)}$

Entretanto, esta convenção se quebra quando queremos avaliar a derivada parcial em um ponto como ${\displaystyle (x,y,z)=(17,u+v,v^{2})}$. Neste caso, a avaliação da função deve ser expressa de uma maneira pouco prática, como:

${\displaystyle {\frac {\partial f(x,y,z)}{\partial x}}(17,u+v,v^{2})}$

ou

${\displaystyle \left.{\frac {\partial f(x,y,z)}{\partial x}}\right|_{(x,y,z)=(17,u+v,v^{2})}}$

a fim de utilizar a notação Leibniz. Assim, nestes casos, pode ser preferível usar a notação do operador diferencial Euler com ${\displaystyle D_{i}}$ como o símbolo derivado parcial em relação à

i-ésima variável.

Por exemplo, poderíamos escrever ${\displaystyle D_{1}f(17,u+v,v^{2})}$ para o exemplo descrito acima, enquanto a expressão ${\displaystyle D_{1}f}$ representa a função derivada parcial em relação à 1ª variável

Para derivadas parciais de ordem superior, a derivada parcial (função) do estilo ${\displaystyle D_{i}f}$ com relação à variável j é designada como ${\displaystyle D_{j}(D_{i}f)=D_{i,j}f}$. Ou seja, ${\displaystyle D_{j}\circ D_{i}=D_{i,j}}$, para que as variáveis sejam listadas na ordem em que as derivadas são tomadas, e assim, em ordem inversa de como a composição dos operadores é normalmente anotada. Naturalmente, o teorema de Clairaut implica que ${\displaystyle D_{i,j}=D_{j,i}}$ desde que as condições de regularidade comparativamente suaves em f sejam satisfeitas.

Antiderivada análoga

Existe um conceito para derivadas parciais que é análogo às antiderivadas para derivadas regulares. Dada uma derivada parcial, ela permite a recuperação parcial da função original.

Considere o exemplo de

${\displaystyle {\frac {\partial z}{\partial x}}=2x+y.}$

A integral "parcial" pode ser tomada com respeito a x (tratando y como constante, de maneira semelhante à diferenciação parcial):

${\displaystyle z=\int {\frac {\partial z}{\partial x}}\,dx=x^{2}+xy+g(y)}$

Aqui, a constante de integração não é mais uma constante, mas uma função de todas as variáveis da função original, exceto x. A razão disso é que todas as outras variáveis são tratadas como constantes quando se toma a derivada parcial, portanto, qualquer função que não envolva ${\displaystyle x}$ desaparecerá quando se toma a derivada parcial, e temos que levar isso em conta quando tomamos o antiderivado. A forma mais geral de representar isto é ter a "constante" representando uma função desconhecida de todas as outras variáveis.

Assim, o conjunto de funções ${\displaystyle x^{2}+xy+g(y)}$, onde g é qualquer função de um documento, representa o conjunto inteiro de funções nas variáveis x,y que poderiam ter produzido a derivada parcial ${\displaystyle 2x+y}$.

Se todas as derivadas parciais de uma função são conhecidas (por exemplo, com o gradiente), então as antiderivadas podem ser combinadas através do processo acima para reconstruir a função original até uma constante. Ao contrário do caso de uma única variável, no entanto, nem todo conjunto de funções pode ser o conjunto de todas as (primeiras) derivadas parciais de uma única função. Em outras palavras, nem todos os campos vetoriais são conservativos.

Derivadas parciais de ordem superior

As derivadas parciais de segunda e maior ordem são definidas de forma análoga às derivadas de ordem superior de funções univariadas. Para a função ${\displaystyle f(x,y,...)}$ a "própria" segunda derivada parcial com respeito a x é simplesmente a derivada parcial da derivada parcial (ambas com respeito a x)

${\displaystyle {\frac {\partial ^{2}f}{\partial x^{2}}}\equiv \partial {\frac {\partial f/\partial x}{\partial x}}\equiv {\frac {\partial f_{x}}{\partial x}}\equiv f_{xx}.}$

A derivada parcial cruzada em relação a x e y é obtida tomando a derivada parcial de f em relação a x, e depois tomando a derivada parcial do resultado em relação a y, para obter

${\displaystyle {\frac {\partial ^{2}f}{\partial y\,\partial x}}\equiv \partial {\frac {\partial f/\partial x}{\partial y}}\equiv {\frac {\partial f_{x}}{\partial y}}\equiv f_{xy}.}$

O teorema de Schwarz afirma que se a segunda derivada é contínua, a expressão para a derivada parcial cruzada não é afetada por qual variável a derivada parcial é tomada em relação à primeira e qual é tomada em segundo lugar. Isto é, a segunda derivada,

${\displaystyle {\frac {\partial ^{2}f}{\partial x\,\partial y}}={\frac {\partial ^{2}f}{\partial y\,\partial x}}}$

ou equivalente ${\displaystyle f_{xy}=f_{yx}.}$

Derivadas parciais próprias e cruzadas aparecem na matriz de Hessian que é usada em condições de segunda ordem em problemas de otimização.