Integral de superfície

Cálculo
Teorema fundamental Limite de funções Continuidade Teorema do valor médio Teorema de Rolle
Cálculo Definições Derivada Diferencial Diferencial de uma função Generalizações da derivada Conceitos Notações para diferenciação Segunda derivada Terceira derivada Mudança de variáveis Derivação implícita Taxas relativas Teorema de Taylor Tabela de derivadas Somas Produto Regra da cadeia Potências Quocientes Fórmula de Faà di Bruno
Cálculo integral Tábua de integrais Definições Primitiva Integral Integral imprópria Integral de Riemann Integral de Lebesgue Integral de linha Integração por partes discos cascas cilíndricas substituição substituição trigonométrica Frações parciais mudança de ordem fórmulas de redução
Série Geométrica Aritmético-geométrica Harmônica Alternada Potências Binomial Taylor Laurent Fourier Testes de convergência Teste da divergência Razão Raiz Integral Comparação direta Comparação no limite Série alternada Condensação de Cauchy Dirichlet Abel
Cálculo vetorial Gradiente Divergência Rotacional Laplaciano Teorema do gradiente Teorema de Green Teorema de Stokes Teorema da divergência Derivada direcional
Cálculo com múltiplas variáveis Formalismo Matriz Tensor Exterior Geométrico Definições Derivada parcial Integral múltipla Integral de linha Integral de superfície Integral de volume Matriz jacobiana
Cálculo especializado Cálculo de variações Fracional Malliavin Estocástico

Uma integral de superfície é uma generalização das integrais múltiplas sobre uma superfície. Dada uma superfície S, pode-se integrar sobre ela um campo escalar ou um campo vetorial. Aplicações de integrais de superfícies aparecem em vários ramos da ciência e das engenharias, tais como em problemas envolvendo fluxo de fluido e de calor, eletricidade, magnetismo, massa e centro de gravidade. Por exemplo, ao integrarmos uma função densidade de massa sobre uma superfície, obteremos a massa aplicada sobre a superfície. Em uma superfície orientável, a integral de superfície do produto interno de um campo vetorial pelo campo normal à superfície fornece o fluxo desse campo, indicado por pela letra grega maiúscula Φ.

Definição

Seja $g:\mathbb {R} ^{3}\to \mathbb {R}$, $g=g(x,y,z)$, uma função definida em todos os pontos de uma superfície $S$. A integral de superfície de $g$ sobre $S$ é definida por:

$$\int \int _{S}gd\sigma$$

onde, $d\sigma$ é o elemento infinitesimal de área sobre a superfície.

Se $S$ é uma superfície orientável, então definimos a integral de superfície de um campo vetorial $F$ sobre $S$ por:

$$\int \int _{S}\mathbf {F} \cdot \mathbf {n} d\sigma$$

onde, $\mathbf {n}$ é o campo normal escolhido na orientação da superfície. O integrando na forma de produto escalar evidencia que somente as componentes do campo perpendiculares à superfície $S$ contribuirão no cálculo do fluxo.

Orientação

Assim como as curvas, também as superfícies precisam ser orientadas, a fim de que, ao adotar certa convenção, sempre se encontre o mesmo sinal para fluxo Φ. Diz-se que uma superfície de dois lados é orientável e que uma superfície de um único lado é não orientável. Assim, existe a necessidade de distinção dos lados de uma superfície orientável e convenção para orientação considerada positiva e negativa, pois ao inverter a orientação de S inverte-se o sinal de Φ.

Sendo assim:

O sinal de ${\overrightarrow {n}}$ serve para orientar $S$.

Para o cálculo de ${\overrightarrow {n}}$:
Suponha que a superfície $S$ seja dada como: $z=g(x,y)$ ou $y=g(x,z)$ ou $x=g(y,z)$.
Reescrevendo cada uma das equações na forma $G(x,y,z)=0$ é possível interpretar a última como a equação de uma superfície de nível de uma função $w=G(x,y,z)$.
A partir do conceito que ${\overrightarrow {\nabla }}G$ é um vetor 3-D e representa um vetor normal à superfície de nível $G(x,y,z)=0$, pode-se definir ${\overrightarrow {n}}$ da seguinte forma:

${\overrightarrow {n}}={\frac {{\overrightarrow {\nabla }}G}{|{\overrightarrow {\nabla }}G|}}$ ou ${\overrightarrow {n}}=-{\frac {{\overrightarrow {\nabla }}G}{|{\overrightarrow {\nabla }}G|}}$

Elemento de área

Elemento de área de uma superfície lisa.

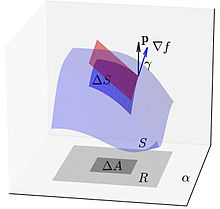
O cálculo do elemento infinitesimal de área sobre a superfície pode ser feito com o auxílio de uma projeção adequada da superfície ${\textstyle S}$ sobre um plano do espaço cartesiano. Suponhamos que ${\textstyle S}$ é descrita pela superfície de nível $f(x,y,z)=c$. Consideremos, ainda, um plano dado ${\textstyle \alpha }$ de normal unitária $\mathbf {p}$. A projeção de $S$ sobre $\alpha$ define uma região planar que denotaremos por ${\textstyle R}$.

Com isso, aproximamos um elemento de área $\Delta S$ da superfície $S$ pela área do elemento tangente associado. Este, por sua vez, pode ser calculado em função do elemento de área $\Delta S$ projetado sobre o plano $\alpha$. Denotando este por $\Delta A$, temos:

$$\Delta S\approx {\frac {1}{|\cos \gamma |}}\Delta A$$

onde, $\gamma$ é o ângulo entre o vetor gradiente $\nabla f$ e o vetor $\mathbf {p}$ calculado em algum ponto de $\Delta S$.

Assim, podemos calcular o elemento de área $d\sigma$ por:

$$d\sigma ={\frac {1}{|\cos \gamma |}}dA$$

onde, $\gamma$ é o ângulo entre o vetor gradiente $\nabla f$ e o vetor $\mathbf {p}$. $dA$ é o elemento de área planar.

Observamos, ainda, que o ângulo $\gamma$ está relacionado ao produto interno entre $\nabla f$ e $\mathbf {p}$ por:

$$\nabla f\cdot \mathbf {p} =|\nabla f||\mathbf {p} |\cos \gamma$$

Segue, daí, que o elemento de área $d\sigma$ pode ser calculado por:

$$d\sigma ={\frac {|\nabla f||\mathbf {p} |}{|\nabla f\cdot \mathbf {p} |}}dA$$

Teorema

Seja $S$ uma superfície suave da forma $z=g(x,y)$ ou $y=g(x,z)$ ou $x=g(y,z)$ e seja ${\overrightarrow {F}}$ um campo vetorial contínuo em $S$. Supondo também que a equação de $S$ seja reescrita como $G(x,y,z)=0$, ao passar $g$ para o membro esquerdo da equação e seja $R$ a projeção de $S$ no plano coordenado das variáveis independentes de $g$. Então:

$$\phi =\int \int _{S}{\overrightarrow {F}}\bullet {\overrightarrow {n}}dS=\pm \int \int _{R}{\overrightarrow {F}}\bullet {\overrightarrow {\nabla }}GdA$$

Cálculo da integral de superfície

Com base no cálculo do elemento de área sobre uma superfície podemos calcular a integral de superfície como uma integral dupla sobre uma região planar. Seja $g:\mathbb {R} ^{3}\to \mathbb {R}$, $g=g(x,y,z)$, uma função definida em todos os pontos de uma superfície $S$ descrita pela superfície de nível $f(x,y,z)=c$. Seja, ainda, $R$ a região planar definida pela projeção de $S$ sobre um plano dado $\alpha$. Então, a integral de superfície de $g$ sobre $S$ pode ser calculada pela seguinte integral dupla sobre $R$:

$$\int \int _{S}gd\sigma =\int \int _{R}g{\frac {|\nabla f||\mathbf {p} |}{|\nabla f\cdot \mathbf {p} |}}dA$$

Observações Importantes

• Já que foi feita substituição de uma integração de superfície por uma integração dupla na região dos planos coordenados, o integrando deve coincidir com os pontos da superfície. É indispensável identificar a superfície.

• Nas aplicações, as superfícies mais simples são os planos, cúbicas, e os tetraedros. Também é possível ter superfícies de revolução, como cilíndricas, e superfícies quádricas.

• É importante a observação do integrando ${\overrightarrow {F}}\bullet {\overrightarrow {\nabla }}G$, para escolha do sistema de coordenadas mais apropriado, tendo em vista a simetria da superfície.

Exemplo

Exemplo da apostila da prof Irene Strauch.

• Calcular o fluxo de ${\overrightarrow {F}}=3z^{2}{\overrightarrow {i}}+6{\overrightarrow {j}}+6xz{\overrightarrow {k}}$ através da superfície $S$ dada por $y=x^{2}$ com $0\leq x\leq 2$ e $0\leq z\leq 3$ e orientada para fora da concavidade.

Resolução

$G(x,y,z)=y-f(x,z)=y-x^{2}$
${\overrightarrow {\nabla }}G(x,y,z)=-2x{\overrightarrow {i}}+{\overrightarrow {j}}$
${\overrightarrow {F}}\bullet {\overrightarrow {\nabla }}G=-6xz^{2}+6$
A região projetada é o retângulo no plano $xz$ restrito a $0\leq x\leq 2$ e $0\leq z\leq 3$, então
$\phi =\int \int _{R}(-6xz^{2}+6)dA$
$\phi =-\int _{0}^{3}\int _{0}^{2}(-6xz^{2}+6)dxdz$
$\phi =-36+(4\cdot 27)=72$

Integral de superfície de campos escalares

Supondo que f seja uma função de um campo escalar de três variáveis em uma superfície suave S. Para encontrar uma fórmula explícita da integral de superficie f sobre S, é precido parametrizar S. Dada a parametrização r(s, t), onde (s, t) varia em alguma região T no plano, a integral de superfície é definida por:

$\iint _{S}f\,\mathrm {d} S=\iint _{T}f(\mathbf {r} (s,t))\left\|{\partial \mathbf {r} \over \partial s}\times {\partial \mathbf {r} \over \partial t}\right\|\mathrm {d} s\,\mathrm {d} t$

Se S for o gráfico de uma função $z=z(x,y)$, então:

${\begin{aligned}\iint _{S}f\,\mathrm {d} S&{}=\iint _{T}f\mathbf {(} x,y,z(x,y)){\sqrt {\left({\partial f \over \partial x}\right)^{2}+\left({\partial f \over \partial y}\right)^{2}+1}}\,\,\mathrm {d} x\,\mathrm {d} y\end{aligned}}$

Onde T é a projeção de S sobre o plano xy.

Integral de superfície de campos vetoriais

O fluxo total através da superfície é encontrado somando-se o produto $\mathbf {F} \cdot \mathbf {n} \;dS$ para cada partição. A medida que os pedaços se tornam infinitamente pequenos, a integral da superfície é ${\textstyle \int _{S}{\mathbf {F\cdot n}}\;dS}$

Seja uma superfície suave $S$ representada por ${\vec {r}}(u,v)=x(u,v){\vec {i}}+y(u,v){\vec {j}}+z(u,v){\vec {k}}$ e ${\vec {n}}={\vec {n}}(u,v)$ um vetor unitário normal a essa superfície. Dado um campo vetorial ${\vec {f}}$ definido sobre $S$, a integral de superfície é definida por:

${\begin{aligned}\iint _{S}\left({\mathbf {\vec {f}} }\cdot {\mathbf {\vec {n}} }\right)\,\mathrm {d} s\ =\iint _{T}{\mathbf {\vec {f}} }(\mathbf {\vec {r}} (s,t))\cdot {\vec {n}}(s,t)\left\|{\frac {\partial \mathbf {r} }{\partial s}}\times {\frac {\partial \mathbf {r} }{\partial t}}\right\|\mathrm {d} s\,\mathrm {d} t\end{aligned}}$

quando a integral da direita existe. Se $S$ é suave por partes, a integral é definida sobre a soma das integrais de cada fragmento de $S$. Como o vetor unitário ${\vec {n}}$ é dado por:

${\begin{aligned}{\vec {n}}={{\frac {\partial \mathbf {r} }{\partial s}}\times {\frac {\partial \mathbf {r} }{\partial t}} \over \left\|{\frac {\partial \mathbf {r} }{\partial s}}\times {\frac {\partial \mathbf {r} }{\partial t}}\right\|}\end{aligned}}$

os módulos do produto vetorial se anulam. A expressão se torna:

${\begin{aligned}\iint _{S}\left({\mathbf {\vec {f}} }\cdot {\mathbf {\vec {n}} }\right)\,\mathrm {d} s\ =\pm \iint _{T}{\mathbf {\vec {f}} }(\mathbf {\vec {r}} (s,t))\left({\frac {\partial \mathbf {r} }{\partial s}}\times {\frac {\partial \mathbf {r} }{\partial t}}\right)\mathrm {d} s\,\mathrm {d} t\end{aligned}}$

A integral terá sinal positivo se o lado de $S$ escolhido para integração for o lado do qual emana o vetor unitário ${\vec {n}}$. Do contrário, o sinal será negativo.

Aplicações

Aplicações de integrais de superfícies aparecem em vários ramos da ciência e das engenharias. Aqui, discutimos rapidamente algumas delas.
Na Mecânica dos Fluidos poderemos ter fluxo de um campo de velocidades ${\vec {v}}$. No Eletromagnetismo teremos fluxo de um campo elétrico ${\vec {E}}$ ou de um campo de indução magnética ${\vec {B}}$ através de uma superfície $S$. Se o campo vetorial for um campo de densidade de corrente, indicado pela letra ${\vec {J}}$, então o fluxo terá dimensão de massa por unidade de tempo ou de corrente elétrica, conforme estejamos estudando o movimento de um fluido ou o movimento de cargas elétricas, respectivamente.

Massa

Suponhamos que $S:f(x,y,z)=c$ descreve a superfície de uma placa fina com densidade de massa dada pela função $\delta =\delta (x,y,z)$. Então, a massa $M$ da placa é dada pela integral de superfície:

$$M=\int \int gd\sigma$$

.

Fluxo

Uma superfície (orientada de acordo com que o fluxo positivo seja atravessando-a de baixo para cima) e linhas de campo atravessando-a.

Seja $S:f(x,y,z)=c$ uma superfície no espaço e ${\vec {F}}$ um campo vetorial. Em cada ponto de S existem dois vetores normais unitários, apontando em direções opostas; o vetor normal unitário com orientação positiva, denotado por ${\hat {n}}$. Se S é uma superfície fechada, como uma esfera ou um cubo, então por convenção ela é orientada de forma que o lado exterior seja o positivo(${\hat {n}}$sempre aponta pra fora de S).

Então o fluxo através de S é determinado por

$$\iint \limits _{S}{\vec {F}}\cdot {\hat {n}}dS$$

onde $dS$ é o elemento de área da superfície

Também é usada a notação ${\vec {dS}}={\hat {n}}dS$

Por exemplo, se ${\vec {F}}$ é o campo de velocidades de um escoamento, então esta integral fornece o fluxo do escoamento através de $S$.

Ver também

• Teorema de Stokes
• Teorema de Gauss