Circunferência

Uma circunferência.

Seções cônicas: A = Parábola, B = Circunferência (parte de baixo do duplo cone) e Elipse (parte de cima), C= Hipérbole

Circunferências em posições relativas.

Parte de uma série sobre:

a constante matemática π

Utilização

Área do círculo · Circunferência · Uso em outras fórmulas

Propriedades

Irracionalidade · Transcendência · Menor que 22/7

Valor

Aproximações · Memorização

Pessoas

Arquimedes · Liu Hui · Tsu Ch'ung Chih · Madhava de Sangamagrama · William Jones · John Machin · John Wrench · Ludolph van Ceulen · Aryabhata

História

Cronologia · Livro

Na cultura

Legislação · Data

Tópicos relacionados

Quadratura do círculo · Problema de Basileia · Tau (τ) · Outros tópicos relacionados a π

Na geometria euclidiana, uma circunferência é o lugar geométrico dos pontos de um plano, que distam (raio) de um ponto fixo (centro).

Equações

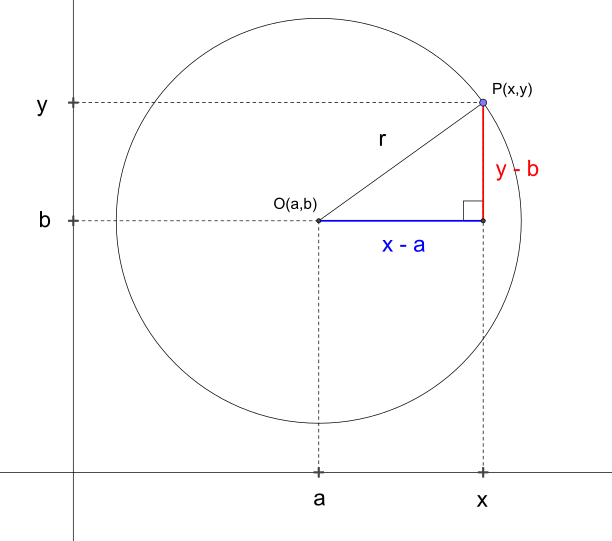
Num sistema de coordenadas cartesianas, uma circunferência pode ser descrita pela equação

$(x-a)^2+(y-b)^2= r^2\,,$

na qual a e b são as coordenadas do centro da circunferência e r é o raio. Caso a circunferência tenha o centro sobre a origem do plano cartesiano, a equação é

$x^2+y^2= r^2\,.$

Também é possível descrever uma circunferência através de equações paramétricas, usando funções trigonométricas:

$x =a + r cos(t)\,$
$y= b + r sen(t)\,.$

Neste caso, t é a variável paramétrica, variando entre 0 e 2π radianos.

Na geometria analítica, pode ser representada através de uma equação da forma Ax² + By² + Cxy + Dx + Ey + F = 0, com coeficientes reais. Sendo que A deve ser igual a B e diferente de zero e C deve ser igual a zero. O raio da circunferência é obtido através da relação:

$R^2=\frac{D^2+E^2 - 4A.F}{4A^2}\,$.

Perímetro

A extensão da circunferência, ou seja, seu perímetro $c\,$ pode ser calculada através da equação:

$c = \pi d = 2 r\ \pi,$

em que $d\,$ é o diâmetro da circunferência, ou seja, o dobro do raio:

$d = 2 r\,.$

Também temos $\pi\,$ que é a constante (pron. pi), cujo valor é

$\pi\,$ = 3,14...

Círculo

O círculo é a área interna delimitada pela circunferência, que pode ser calculada usando a equação:

$a = \pi r^2\,.$

Seção Cônica

A circunferência é a curva plana fechada que se obtém quando da interseção de um cone circular reto com um plano paralelo à sua base.

Ver também

• Lugares Geométricos
• Círculo
• Diâmetro
• Trigonometria