Geometria euclidiana

Na matemática, geometria euclidiana é a geometria, em duas e três dimensões, baseada nos postulados de Euclides de Alexandria.
História[editar | editar código-fonte]
A geometria euclidiana teve sua origem com o grande matemático Euclides de Alexandria[1]. Nascido aproximadamente em 330 a.C. na Síria, ele realizou seus estudos na cidade de Atenas onde frequentou a Academia de Platão. A pedido do rei, Ptolomeu I governante do Egito entre 323 a.C. à 283 a.C. foi convidado a estudar Matemática na academia de Alexandria também conhecida como “Museu”. Com o passar do tempo ganhou destaque pela forma que ele ensinava Geometria e Álgebra. Essas disciplinas já eram de conhecimento pelos matemáticos anteriores a Euclides, porém ele fez um estudo mais aprofundado dos conteúdos, os organizou de forma lógica e as condensou, instituindo a característica grega do Rigor Científico e criando uma das maiores obras primas da Matemática, denominada “Os Elementos”. Esta obra é constituída por treze livros que contemplam tópicos como aritmética, geometria e álgebra.[2]
O texto de "Os elementos"[3] foi a primeira discussão sistemática sobre a geometria e o primeiro texto a falar sobre teoria dos números. Foi também um dos livros mais influentes na história, tanto pelo seu método quanto pelo seu conteúdo matemático. O método consiste em assumir um pequeno conjunto de axiomas intuitivos e, então, provar várias outras proposições (teoremas) a partir desses axiomas. Muitos dos resultados de Euclides já haviam sido afirmados por matemáticos gregos anteriores, porém ele foi o primeiro a demonstrar como essas proposições poderiam ser reunidas juntas em um abrangente sistema dedutivo.
A teoria desenvolvida através deste livro foi uma das mais importantes da Matemática, ela foi adotada por muitos como base para estudar a Geometria. A partir do final do Século XIX para o inicio do Século XX foi instituída a disciplina de Geometria Euclidiana seguindo a axiomática instituída por Euclides que se distingue por apresentar um espaço que não se modifica em momento algum, revela uma estrita simetria, se uma relação for verdadeira para “a” e “b” tomadas nessa ordem também será para “b” e “a” nesta ordem. Essa teoria atravessou a Idade Média e o Renascimento como representação do conhecimento clássico, a partir da Idade Moderna o modelo euclidiano foi substituído por outras geometrias.
A base da geometria euclidiana: os axiomas e postulados[editar | editar código-fonte]
A geometria euclidiana tem sua base em axiomas e postulados. Para Aristóteles, axiomas são verdades incontestáveis aplicadas a todas as ciências e os postulados eram verdades sobre um determinado tema (neste caso, a geometria) e foi assim também usado por Euclides. Ao todo, são dez proposições que utilizam os conceitos de ponto, intermediação e congruência. Toda geometria que satisfaz a todos eles é considerada euclidiana.
Os axiomas[2] são:
- Axioma 1: Coisas que são iguais a uma mesma coisa, são iguais entre si.
- Axioma 2: Se iguais são adicionados a iguais, os resultados são iguais.
- Axioma 3: Se iguais são subtraídos de iguais, os restos são iguais.
- Axioma 4: Coisas que coincidem uma com a outra, são iguais.
- Axioma 5: O todo é maior do que qualquer uma das suas partes.
Os axiomas não são passíveis de demonstração por serem evidentemente verdadeiros. Os postulados surgem com o desenvolvimento dos axiomas e, se provados verdadeiros, são considerados teoremas[3].
Estes são os seguintes:
- Postulado 1: Dados dois pontos distintos, há um único segmento de reta que os une;
- Postulado 2: Um segmento de reta pode ser prolongado indefinidamente para construir uma reta;
- Postulado 3: Dados um ponto qualquer e uma distância qualquer, pode-se construir uma circunferência de centro naquele ponto e com raio igual à distância dada;
- Postulado 4: Todos os ângulos retos são congruentes (semelhantes);
- Postulado 5: Se duas linhas intersectam uma terceira linha de tal forma que a soma dos ângulos internos em um lado é menor que dois ângulos retos, então as duas linhas devem se intersectar neste lado se forem estendidas indefinidamente. (Postulado de Euclides ou Postulado das Paralelas)
Definições iniciais[editar | editar código-fonte]
Euclides fez algumas definições para que a geometria tivesse sentido e pudesse provar suas proposições, no total foram 23 definições:
- Ponto é aquilo de que nada é parte;
- Linha é comprimento sem largura;
- Extremidades de uma linha são pontos;
- Linha reta é a que está posta por igual com os pontos sobre si mesma;
- Superfície é aquilo que tem somente comprimento e largura;
- Os lados de uma superfície são linhas;
- Superfície plana é a que esta posta por igual com retas sobre si mesma;
- Ângulo plano é a inclinação, entre elas, de duas linhas no plano, que se tocam e não estão postas sobre uma reta;
- Quando as linhas que contêm o ângulo sejam retas, o ângulo é chamado de retilíneo;
- Quando uma reta, tendo sido alterada sobre uma reta, faça os ângulos adjacentes iguais, cada um dos ângulos é reto, e a reta que se alteou é chamada uma perpendicular àquela sobre a que se alteou;
- Ângulo obtuso é o maior do que um reto;
- Agudo, o menor que um reto;
- Fronteira é aquilo que é extremidade de alguma coisa.
- Figura é o que é contido por alguma ou algumas fronteiras;
- Círculo é uma figura plana contida por uma linha [ que é chamada circunferência ], em relação a qual todas as retas que a encontram [ até a circunferência do círculo ], a partir de um ponto dos postos no interior da figura, são iguais entre si;
- O ponto é chamado de centro do círculo;
- Diâmetro do círculo é alguma reta traçada através do centro, e terminando, em cada um dos lados, pela circunferência do círculo, e que corta o círculo em dois;
- Semicírculo é a figura contida tanto pelo diâmetro quanto pela circunferência cortada por ele. E centro do semicírculo é o mesmo do círculo.
- Figuras retilíneas são as contidas por retas, por um lado, triláteras, e por três, e, por outro lado, quadriláteras, as por quatro, enquanto multiláteras, as contidas por mais do que quatro retas;
- Das figuras triláteras, por um lado, triângulo equilátero é o que tem os três lados iguais, e, por outro lado, isósceles, o que tem dois lados iguais, enquanto escaleno, o que tem três lados desiguais;
- Ainda das figuras trilateras, por um triângulo retângulo é o que tem um ângulo reto, e, por outro lado, obtusângulo, o que tem um ângulo obtuso, enquanto acutângulo, o que tem três ângulos agudos;
- Das figuras quadriláteras, por um lado, quadrado é aquela que é tanto equilátera quanto retangular, e, por outro lado, oblongo, a que, por um lado, é retangular, e, por outro lado, não é equilátera, enquanto losango, e que, por um lado, é equilátera, e, por outro lado, não é retangular, e romboide, a que tem tantos os lados opostos quantos os ângulos opostos iguais entre si, a qual não é equilátera nem retangular; e as quadriláteras, além dessas, sejam chamadas trapézios;
- Paralelas são retas que, estão no mesmo plano, e sendo prolongadas ilimitadamente em cada um dos lados, em nenhum se encontram.
A partir dessas definições, dos axiomas e postulados, Euclides fez várias demonstrações. Vejamos como ele demonstrou as seguintes proposições:
- Construir um triângulo equilátero sobre uma reta limitada dada. (proposição 1)
“Seja a reta limitada dada AB. É preciso, então, sobre a reta AB construir um triângulo equilátero.
Fique descrito, por um lado, com o centro A, e por outro lado, com a distância AB, o circulo BCD, e, de novo, fique descrito, por um lado, com o centro B, e, por outro lado, com a distancia BA, o circulo ACE, e, a partir do ponto C, no qual os círculos se cortam, até os pontos A, B, fiquem ligadas as retas CA, CB.
E, como o ponto A é centro do circulo CDB, a AC é igual à AB; de novo, como o ponto B é centro do circulo CAE, a BC é igual à BA. Mas a CA foi também provada igual à AB; portanto, cada uma das CA, CB é igual à AB. Mais as coisas iguais à mesma coisa são também iguais entre si; portanto, também a CA é igual à CB, portanto, as três CA, AB, BC são iguais entre si.
Portanto, o triângulo ABC é equilátero, e foi construído sobre a reta limitada dada AB.”
Com o auxílio do 1º e 3º postulados, mais as definições 15 e 20 ele provou a proposição acima.
- Pelo ponto dado, traçar uma linha reta paralela à reta dada. (proposição 31)
“Sejam, por um lado, o ponto A, e, por outro lado, a reta dada BC; é preciso, então, pelo ponto A, traçar uma linha reta paralela à reta dada BC.
Fique tomado, sobre a BC, o ponto D, encontrado ao acaso, e fique ligada a Ad; e fique construído, sobre a reta DA e no ponto A sobre ela, o sob DAE igual ao ângulo sob ADC; e fique prolongada a reta AF sobre uma reta com a EA.
E, como a reta AD, caindo sobre as duas retas BC, EF, fez os ângulos sob EAD, ADC, alternos, iguais entre si, portanto, a EAF é paralela à BC.
Portanto, pelo ponto dado A, foi traçada a linha reta EAF paralela à reta dada BC; o que era preciso fazer.”
Com o auxílio dos postulados 1 e 2 e também usando as proposições 23 e 24 ele provou esta proposição.
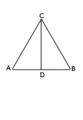
- Cortar em duas a reta limitada dada. ( proposição 10)
Seja a reta dada AB; é preciso, então, cortar a reta limitada AB em duas.
Fique construído sobre ela o triângulo equilátero ABC, e fique cortado o ângulo sob ACB em dois pela reta CD; digo que a reta AB foi cortada em duas no ponto D.
Pois, como a AC é igual à CB, e a CD é comum, então, as duas AC, CD são iguais às duas BC, CD, cada uma a cada uma; e o ângulo sob ACD é igual ao ângulo sob BCD; portanto, a base AD é igual à base BD.
Portanto, a reta limitada dada AB foi cortada em duas no D; o que era preciso fazer.
Com o auxílio da definição 20 e também usando as proposições 1, 4 e 9 ele provou esta proposição.
- As paralelas à mesma reta são paralelas entre si. ( proposição 30)
Seja cada uma das AB, CD paralelas à EF; digo que também a AB é paralela à CD. Caia, pois, a reta GK sobre elas. E, como a reta GK caiu sobre as retas paralelas AB, EF, portanto, sob AGK é igual ao sob GHF. De novo,como a reta GK caiu sobre as paralelas EF, CD, o sob GHF é igual ao sob GKD. Mais foi provado também o sob AGK igual ao sob GHF. Portanto, também o sob AGK é igual ao sob GKD; e são alternos. Portanto, a AB é paralela à CD.
Portanto, as paralelas à mesma reta são paralelas entre si; o que era preciso provar.
Com o auxílio das proposições 27 e 29 a proposição acima foi provada. Até os dias atuais é utilizado essas ferramentas para resolver problemas de geometria euclidiana.
- Em todo o triângulo retângulo o quadrado feito sobre o lado oposto ao ângulo reto, é igual aos quadrados formados sobre os outros lados, que fazem o mesmo ângulo reto. (Proposição 47)
Seja um triângulo retângulo ABC, cujo ângulo BÂC é reto. Nos segmentos AB, BC e AC construir os quadrados ABFG, BDEC e ACHI, respectivamente (proposição 46). Do ponto A, trace uma paralela AL ao segmento BD (proposição 31). Trace os segmentos FC e AD. Por serem retos, os ângulos ABF e CBD são congruentes, junte a eles o ângulo ABC, então os ângulos CBF e ABD são congruentes (axioma 2). Pela proposição 4, os triângulos CBF e ABD são congruentes, pelo critério lado, ângulo e lado. Por estar na mesma base BD e entre as mesmas paralelas BD e AL, o paralelogramo BL possui o dobro da área do triângulo ABD (proposição 41). Por estar na mesma base FB e entre as mesmas paralelas FB e GC, o quadrado ABFG possui o dobro da área do triângulo CBF (proposição 41). Logo, pelo axioma 6, o quadrado ABFG possui a mesma área que o paralelogramo BL. Seguindo o mesmo raciocínio, traçando o segmento AE e HB, o quadrado ACHI possui a mesma área do paralelogramo CL.
Portanto, Em todo o triângulo retângulo o quadrado feito sobre o lado oposto ao ângulo reto, é igual aos quadrados formados sobre os outros lados, que fazem o mesmo ângulo reto.
Com o auxílio das proposições 46, 31, 4 e 41 e dos axiomas 2 e 6 ele provou essa proposição.
O quinto postulado[editar | editar código-fonte]
O quinto postulado da geometria euclidiana por muitos anos foi alvo de tentativas de prova por vários matemáticos, porém essa demonstração jamais foi alcançada. As tentativas tinham o intuito de demonstrá-lo sem o auxílio de outra proposição que utilizava o mesmo princípio, logo abaixo está a tentativa de Nasiredin[4], (1201 - 1274), ou Nasir Eddin al-Tusi, astrônomo e matemático persa, que compilou uma versão árabe dos Elementos de Euclides:
”ele parece ter sido o primeiro a dirigir sua atenção para a importância, no estudo do Quinto Postulado, do teorema da soma dos ângulos de um triângulo”.
Inicialmente, Nasiredin considera, sem provar, a seguinte afirmação:
Sejam os pontos A e B, respectivamente, sobre as retas r e s, de modo que AB é perpendicular à r e forma um ângulo agudo α com s. Então as perpendiculares baixadas de s sobre r dos lado do ângulo agudo, são menores que AB, e as perpendiculares baixadas do outro lado são maiores que AB. Além disto os ângulos que essas perpendiculares formam com s na mesma direção de α são também agudos. Esta afirmação significa que EF > AB > CD, e os ângulos β e γ são agudos.
A partir daí, Nasiredin considera um quadrilátero ABCD, onde os lados AD e BC são congruentes e perpendiculares ao lado AB. Se o ângulo BCD é agudo, pela afirmação considerada AD é menor que BC, contrariando a hipótese. Se BCD é obtuso, ent˜ao AD é maior que BC, que também é absurdo. Logo BCD deve ser reto. Analogamente, ADC também deve ser reto.
Assim, traçando a diagonal BD formam-se dois triângulos congruentes cuja soma dos ângulos internos é igual a 180º. O primeiro erro de Nasiredin está nas suposições feitas inicialmente, quando considera que as retas r e s convergem do lado do ângulo agudo. Isto não é necessariamente verdade sem o uso do quinto postulado. Depois, quando assume que o ângulo DCB é agudo, n˜ao pode-se concluir que o ângulo CDA é obtuso. Na verdade, posteriormente, será visto que o matemático Girolamo Saccheri, utiliza este quadrilátero para fazer a sua demonstração do quinto postulado, e mostra que os ângulos ADC e BCD são congruentes.
Sem alcançar êxito na demonstração do quinto postulado de Euclides, foram criadas as geometrias que adotaram os quatro postulados anteriores e fizeram suas adaptações para o quinto postulado, criando as geometrias não euclidianas, essas novas geometrias são chamadas de geometrias hiperbólicas e elíptica.
Ver também[editar | editar código-fonte]
- Axiomas de Hilbert
- Geometria algébrica
- Geometria descritiva
- Geometria elíptica
- Geometria esférica
- Geometria fractal
- Geometria não euclidiana
- Lugares geométricos
- Plano euclidiano
- Postulado das paralelas