Comprimento do arco
A determinação do comprimento de segmentos de arco irregular — também conhecido como retificação de uma curva — representou uma dificuldade histórica. Embora muitos métodos tenham sido utilizados para curvas específicas, o advento do cálculo levou a uma formulação geral que provê a solução em alguns casos.
Definição precisa[editar | editar código-fonte]
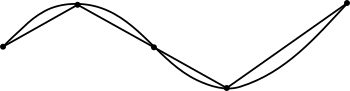
Escolher um finito número de pontos ao longo de uma curva e conectar cada um destes pontos com o próximo com uma linha reta. A soma do comprimento de cada um destes segmentos é o comprimento de um caminho polinomial.
Definição: O comprimento de uma curva é o menor número tal que o comprimento dos caminhos polinomiais nunca pode ultrapassar, não importando quanto juntos sejam colocados os pontos finais do segmentos.
Na linguagem matemática, o comprimento do arco é o supremo de todos comprimentos de um dado caminho polinomial.
Métodos modernos[editar | editar código-fonte]
Considere uma função tal que e (isto é a derivada em relação a x) são contínuas em [a, b] . O comprimento s de parte do gráfico de f entre x = a e x = b é dado pela fórmula:
a qual se deriva da fórmula da distância aproximada do comprimento do arco composto de muitos pequenos segmentos de reta. Como o número de segmentos tende para o infinito (pelo uso da integral) esta aproximação se torna um valor exato.
Se a curva é definida parametricamente por e , então o comprimento do arco entre t = a e t = b é[1]
Deve-se notar que a definição acima só pode ser considerada rigorosa caso se prove que duas parametrizações distintas geram o mesmo comprimento de arco.
Método vetorial[editar | editar código-fonte]
Seja uma partição equidistante do domínio com e , , pontos sobre a curva. Uma possível aproximação para o comprimento da curva é dado pelo comprimento da poligonal. Observe que o comprimento do segmento é dado por , logo, a aproximação para o comprimento da curva é
Naturalmente, . Como o lado direito da última igualdade é uma soma de Riemann, temos:
Logo, o comprimento do arco S quando a parâmetro corre de a até t é:
Ver também[editar | editar código-fonte]
Notas[editar | editar código-fonte]
- ↑ Carmo (2010), p. 7.
Referências[editar | editar código-fonte]
- Carmo, Manfredo Perdigão do (2010). Geometria Diferencial de Curvas e Superfícies 4 ed. Rio de Janeiro: SBM. ISBN 978-85-85818-26-5



![{\displaystyle s=\int _{a}^{b}{\sqrt {1+[f'(x)]^{2}}}\,dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa1bddf484dfabb54bd6e55a935c3ffc927ea2ce)


![{\displaystyle s=\int _{a}^{b}{\sqrt {[X'(t)]^{2}+[Y'(t)]^{2}}}\,dt.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2cad557ab34657ea6b9a25ddf62b0d82571c38f8)












