Logaritmo

Na matemática, o logaritmo de um número é o expoente a que outro valor fixo, a base, deve ser elevado para produzir este número.[3] Por exemplo, o logaritmo de 1 000 na base 10 é 3 porque 10 elevado ao cubo é 1 000 (1 000 = 10 × 10 × 10 = 103). De maneira geral, para quaisquer dois números reais b e x, onde b é positivo e b ≠ 1,[4]
- .
O logaritmo da base 10 (b = 10) é chamado de logaritmo comum (ou decimal) e tem diversas aplicações na ciência e engenharia. O logaritmo natural (ou neperiano) tem a constante irracional e (≈ 2,718) como base e é utilizado na matemática pura, principalmente em cálculo diferencial. Ainda há o logaritmo binário, no qual se usa base 2 (b = 2), que é importante para a ciência da computação.[5]
O conceito de logaritmo foi introduzido por John Napier no ano de 1614, a fim de simplificar cálculos, daí a nomenclatura logaritmo neperiano.[6] Ele foi rapidamente adotado por navegadores, cientistas, engenheiros e outros profissionais para facilitar seus cálculos, através do uso de réguas de cálculo e tabelas logarítmicas. Algumas etapas tediosas da multiplicação com vários dígitos podem ser substituídas por consultas a tabelas ou por somas mais simples devido ao fato de o logaritmo de um produto ser o somatório dos logaritmos dos fatores:[7]
- desde que b, x e y sejam positivos e b ≠ 1.
A atual noção de logaritmo advém de Leonhard Euler, que o relacionou com a função exponencial no século XVIII.[8] As escalas logarítmicas permitem reduzir grandezas de elevada amplitude para valores menores. Por exemplo, o decibel é uma unidade logarítmica que indica a proporção de uma quantidade física (geralmente energia ou intensidade) em relação a um nível de referência, isto é, estabelece uma razão entre a quantificação da energia liberada e a amplitude.[9] Em química, o potencial hidrogeniônico (pH) mede a acidez e a alcalinidade de soluções aquosas. Os logaritmos ainda são comuns em fórmulas científicas, na teoria da complexidade computacional e de figuras geométricas chamadas fractais.[10][11] Eles descrevem intervalos musicais, aparecem em fórmulas que contam os números primos, informam vários modelos da psicofísica e podem auxiliar na perícia contábil.[12]
Do mesmo modo como o logaritmo é o inverso da exponenciação, o logaritmo complexo é a função inversa da função exponencial aplicada a números complexos. O logaritmo discreto é outra variante; ele é utilizado na criptografia assimétrica.[13]
Razão e definição[editar | editar código-fonte]
A ideia dos logaritmos é reverter a operação de exponenciação, isto é, elevar um número a uma potência.[14] A título de exemplo, a potência de três (ou o cubo) de 2 é 8, porque 8 é o produto dos três fatores de 2:[15]
Disso resulta que o logaritmo de 8 na base 2 é 3, ou seja:[16] log2 8 = 3.
Exponenciação[editar | editar código-fonte]
A potência de três de qualquer número b é o produto de três fatores de b. De forma mais geral, elevar b à enésima potência, quando n é um número natural, se realiza pela multiplicação de n fatores de b. A enésima potência de b é escrita como bn, que significa:[17]
A exponenciação pode ser estendida para by, onde b é um número positivo e o expoente y é qualquer número real.[18] Por exemplo, b−1 é o inverso de b, ou seja, 1/b.[19]
Definição[editar | editar código-fonte]
O logaritmo de um número positivo real , na base , é o expoente pelo qual deve ser elevado para se chegar a , sendo um número positivo real diferente de .[20] Em outras palavras, o logaritmo de na base é a solução de na equação : [21]
- onde
- é a base do logaritmo;
- é o logaritmando;
- é o próprio logaritmo;
- Sendo pronunciado como "o logaritmo de na base ".[22]
Exemplos[editar | editar código-fonte]
, visto que .
Os logaritmos também podem ser negativos:[23]
porque:
Um terceiro exemplo é: log10(150) é aproximadamente 2,176, que se localiza entre 2 e 3, da mesma forma como 150 está entre 102 = 100 e 103 = 1 000.[25] Finalmente, para qualquer base b, logb(b) = 1 e logb(1) = 0, pois b1 = b e b0 = 1, respectivamente.[26]
Identidades logarítmicas[editar | editar código-fonte]
Várias fórmulas são importantes para relacionar um logaritmo a outro, e essas relações são chamadas de identidades logarítmicas ou leis de log.[27]
Produto, quociente, potência e raiz[editar | editar código-fonte]
A tabela a seguir lista algumas identidades logarítmicas[28] com exemplos, sendo que todas podem ser derivadas após a substituição da definição de logaritmo e/ou nos primeiros membros.[29]
| Fórmula[30] | Descrição | Exemplo | |
|---|---|---|---|
| produto | O logaritmo de um produto é a soma dos logaritmos dos números a serem multiplicados | ||
| quociente | O logaritmo da razão é a diferença dos logaritmos | ||
| potência no logaritmando | O logaritmo da p-ésima potência de um número é p vezes o logaritmo do número em questão | ||
| raiz | A p-ésima raiz de um número é o logaritmo do número dividido por p. |
Mudança de base[editar | editar código-fonte]
O logaritmo logb(x) pode ser calculado a partir dos logaritmos de x e de b, ambos com uma base arbitrária k, utilizando a seguinte fórmula:[31][32]
As típicas calculadoras científicas calculam os logaritmos nas bases 10 e e.[33] Logaritmos com respeito a qualquer base b podem ser determinados usando qualquer um desses logaritmos, segundo a fórmula:[34]
Dado um número x e seu logaritmo logb(x), a base desconhecida b é dada por:[35]
Bases particulares[editar | editar código-fonte]
Entre todas as opções para a base, três são particularmente comuns. Essas são 10, 2 e a constante irracional e. Na análise matemática, o uso do logaritmo de base e é generalizado por causa de suas particulares propriedades analíticas. Por outro lado, o uso da base 10 é mais fácil para cálculos manuais no sistema de números decimais.[36]
Assim, log10(x) está relacionado com o número de dígitos decimais de um inteiro positivo x, isto é, o número de dígitos é o menor número inteiro estritamente maior que log10(x).[37] Por exemplo, log10(1 430) é aproximadamente 3,15: o próximo inteiro é 4, que é a quantidade de dígitos de 1 430. Tanto o logaritmo natural quanto o logaritmo binário são utilizados na teoria da informação, o que corresponde respectivamente ao uso de nats ou bits como unidades fundamentais de informação.[38] Os logaritmos de base 2 também se encontram na ciência da computação, na teoria musical e na fotografia.[39]
| Base b | Nome do logb(x) | Notação ISO[40][41] | Outras notações | Usado em |
|---|---|---|---|---|
| 2 | logaritmo binário | lb(x)[42] | ld(x), log(x), lg(x), log2(x) | ciência da computação, teoria da informação, teoria musical, fotografia |
| e | logaritmo natural | ln(x)[43] | log(x)[44][45] | matemática, física, química, estatísticas, economia, teoria da informação e alguns campos da engenharia |
| 10 | logaritmo comum | lg(x) | log(x), log10(x) | engenharia, ondulatória, pH, escalas, tábuas logarítmicas, calculadoras e espectroscopia |
História[editar | editar código-fonte]
Antecessores[editar | editar código-fonte]
Os babilônios, entre os anos de 2000–1600 a.C., podem ter inventado a multiplicação dos quadrados dos quartos para multiplicar dois números utilizando somente a adição, a subtração e uma tabela de quadrados dos quartos.[46][47] Entretanto, ele não poderia ser usado para divisão sem uma tabela adicional dos inversos (ou o conhecimento de um algoritmo suficientemente simples para gerar os inversos). Grandes tabelas de quadrados dos quartos foram utilizadas para simplificar a multiplicação precisa de grandes números a partir de 1817, até este método ser substituído pela utilização dos computadores.[48]
O matemático indiano Virasena trabalhou com o conceito de ardhaccheda, o número de vezes em que um número da forma 2n pode ser dividido por 2. Para potências exatas de 2, este é o logaritmo naquela base, que é um número inteiro; para outros números, ele é indefinido. Ele descreveu relações como a fórmula do produto e também introduziu logaritmos inteiros nas bases 3 (trakacheda) e 4 (caturthacheda).[49]
Michael Stifel publicou Arithmetica integra em Nuremberg em 1544, contendo uma tabela de inteiros e potências de 2, sendo considerada uma versão inicial da tabela logarítmica.[50]
No final do século XVI e início do século XVII, um algoritmo chamado prosthaphaeresis foi usado para aproximar a multiplicação e a divisão. Isto usava a identidade trigonométrica[51][52]
ou similar para converter as multiplicações em adições, bem como consultas a tabelas. Entretanto, os logaritmos são mais diretos e requerem menos trabalho. Pode-se demonstrar, com o uso da Fórmula de Euler, que os dois métodos são relacionados.
De Napier a Euler[editar | editar código-fonte]

O método dos logaritmos foi proposto publicamente em 1614 por John Napier, em um livro intitulado Mirifici Logarithmorum Canonis Descriptio (Descrição da maravilhosa regra dos logaritmos).[53][54] Joost Bürgi construiu uma tabela de potências com base muito próxima a 1, e esta tabela fornecia uma boa correspondência entre os inteiros 1-10 (ou 10-100, etc.) e expoentes que podiam ser somados. Esta tabela foi impressa (mas talvez não publicada) em 1620. Entretanto, Bürgi não definiu uma função abstrata contínua como Napier, e também não resolveu a precisão das interpolações, o que também foi trabalhado por Napier.
Johannes Kepler, que usou tabelas de logaritmos extensivamente para compilar o seu Ephemeris, que depois dedicou a Napier,[55][55] observou:
…a ênfase em cálculo levou Justus Byrgius [Joost Bürgi] pelo caminho para esses logaritmos muitos anos antes de o sistema de Napier aparecer; mas... em vez de apresentar seu filho para o benefício do público, ele o abandonou no nascimento.Original {{{{{língua}}}}}: Rudolphine Tables (1627)— Johannes Kepler[56]
Por meio de subtrações repetidas, Napier calculou (1 − 10−7)L para L variando de 1 a 100. O resultado para L=100 é aproximadamente 0,99999 = 1 − 10−5. Napier então calculou os produtos desses números com 107(1 − 10−5)L para L de 1 a 50, e fez similarmente com 0,9998 ≈ (1 − 10−5)20 e 0,9 ≈ 0,99520. Esses cálculos, que levaram vinte anos, permitiram-lhe fornecer, para qualquer número N de 5 a 10 milhões, o número L que resolve a equação
Napier primeiro chamou L um “número artificial”, mas depois introduziu o termo “logaritmo” para significar um número que indica uma razão: λόγος (logos) significando proporção, e ἀριθμός (arithmos) significando número. Em notação moderna, a relação para logaritmos naturais é:[57]
onde uma boa aproximação corresponde à observação que
A invenção dos logaritmos foi rápida e amplamente recebida com elogios. Os trabalhos de Bonaventura Cavalieri (Itália), Edmund Wingate (França), Xue Fengzuo (China) e Johannes Kepler (Alemanha) ajudaram a espalhar e expandir ainda mais o conceito e a utilidade dos logaritmos.[58]
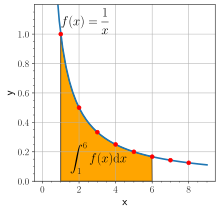
Em 1649, Alphonse Antonio de Sarasa, antigo aluno de Grégoire de Saint-Vincent, relacionou os logaritmos com a quadratura da hipérbole, apontando que a área f(t) do gráfico de x = 1 a x = t satisfaz[59][60]
O logaritmo natural foi descrito primeiramente pelo alemão Nikolaus Mercator em sua obra Logarithmotechnia,[61] publicada em 1668, embora o professor de matemática John Speidell, em 1619, já tivesse elaborado uma tabela explicando o que eram os logaritmos naturais com base no trabalho de Napier.[62] Por volta de 1730, Leonhard Euler definiu a função exponencial e o logaritmo natural por
Euler também mostrou que uma função é o inverso da outra.[64][65][66]
Tabelas de logaritmos[editar | editar código-fonte]

Com a simplificação de cálculos difíceis, os logaritmos contribuíram para o avanço da ciência, especialmente da astronomia. Foram críticos para os avanços na agrimensura, na navegação astronômica e em outros domínios.[67] Pierre Simon Laplace comentou sobre os logaritmos:
- "... um admirável artifício que, ao reduzir para poucos dias um trabalho de muitos meses, duplica a vida dos astrônomos e poupa-os dos erros e desgostos inseparáveis dos longos cálculos."[68]
A ferramenta-chave que possibilitou o uso prático dos logaritmos antes das calculadoras e computadores foi a tabela de logaritmos.[69] A primeira tabela deste tipo foi compilada por Henry Briggs em 1617, imediatamente após a invenção de Napier. Ulteriormente, tabelas com maior alcance e precisão foram publicadas. Essas tabelas listavam valores de logb(x) e bx para qualquer número x em um certo intervalo, com uma determinada precisão, para uma certa base b (usualmente, b = 10). Por exemplo, a primeira tabela de Briggs contém o logaritmo comum de todos os números inteiros de 1 a 1 000, com precisão de oito dígitos. Como a função f(x) = bx é a função inversa de logb(x), ela foi chamada de antilogaritmo.[70] O produto e o quociente de dois números positivos c e d eram rotineiramente calculados pela soma e diferença de seus logaritmos. O produto cd ou o quociente c/d são encontrados por meio de consulta aos antilogaritmos da soma ou diferença, na mesma tabela:
e
Para cálculos manuais que demandam precisões apreciáveis, realizar a pesquisa dos dois logaritmos (na tabela logarítmica), realizar sua soma ou diferença e localizar o antilogaritmo na tabela[71] é muito mais rápido do que a multiplicação por métodos anteriores, tal como o prosthaphaeresis, que depende das identidades trigonométricas. Cálculos de potências e raízes são reduzidos à multiplicação ou à divisão da seguinte maneira:[72]
e
Muitas tabelas de logaritmos fornecem os logaritmos separadamente pela característica e a mantissa de x, ou seja, a parte inteira e a parte fracionária de log10(x).[73] A característica de 10 · x é 1 mais a característica de x, e seus significandos são os mesmos. Isso estende o escopo das tabelas de logaritmos: dada uma tabela listando log10(x) para todos os inteiros de 1 a 1 000, o logaritmo de 3 542 é aproximadamente:[74]
Régua de cálculo[editar | editar código-fonte]
Outra aplicação crítica foi a régua de cálculo, um par de escalas logarítmicas utilizadas para cálculos, da seguinte maneira:[75]

A escala logarítmica não deslizante de Edmund Gunter foi desenvolvida logo depois da invenção de Napier. O padre inglês William Oughtred a aprimorou para criar a régua de cálculo — um par de escalas logarítmicas móveis, em que os números são colocados em distâncias proporcionais às diferenças de seus logaritmos. Deslizando-se a escala superior em relação à escala inferior permite a soma mecânica dos logaritmos.[76] Por exemplo, colocando-se a distância de 1 a 2 na escala inferior e a distância de 1 a 3 na escala superior, chega-se na escala inferior ao produto 6.[77] A régua de cálculo foi uma ferramenta essencial para engenheiros e cientistas até a década de 1970, porque ela permite, em detrimento da precisão, muito mais rapidez no cálculo que as técnicas baseadas nas tabelas logarítmicas.[64]
Propriedades analíticas[editar | editar código-fonte]
Um estudo mais profundo dos logaritmos requer o conceito de função: uma relação entre dois conjuntos, na qual há uma condição entre cada um de seus elementos. Um exemplo é a função exponencial, na qual a enésima potência de b resulta em um número real y.[78] Esta função se escreve:
Função logarítmica[editar | editar código-fonte]
Para justificar a definição de logaritmo, é necessário mostrar que a equação tem a solução x e que esta é única, desde que y seja positivo e b seja positivo e diferente de 1. Uma prova para este fato requer o teorema do valor intermediário do cálculo elementar.[79] Este teorema afirma que uma função contínua que produz dois valores m e n também produz qualquer valor que se situe entre m e n.[80] Uma função é contínua quando ela não dá “saltos”, isto é, quando seu gráfico pode ser desenhado sem se levantar a caneta.
Pode-se demonstrar que esta propriedade se aplica à função f(x) = bx. Como f assume valores positivos arbitrariamente grandes e arbitrariamente pequenos, qualquer número y > 0 situa-se entre f(x0) e f(x1) para apropriados x0 e x1.[81] Logo, o teorema do valor intermediário garante que a equação f(x) = y tem uma solução. Além disso, há apenas uma solução para essa equação, porque a função f é estritamente crescente (para b > 1) ou estritamente decrescente (para 0 < b < 1).[82]
A única solução x é o logaritmo de y na base b, logb(y). A função que atribui a y o seu logaritmo é chamada de função logarítmica ou, simplesmente, logaritmo. A função logb(x) é essencialmente caracterizada pela fórmula do produto:[83]
Mais precisamente, o logaritmo em qualquer base b > 1 é a única função crescente f dos números reais para os reais que satisfaçam f(b) = 1 e [84]
Teorema — Dado um número real b (com 0 < b ≠ 1), chama-se função logarítmica a função f de ℝ+* em ℝ dada pela lei f(x) = logb(x).[85]
Função inversa[editar | editar código-fonte]

A fórmula para o logaritmo de uma potência indica que para qualquer número x,
Literalmente, tendo-se a x-ésima potência de b, o logaritmo na base b resulta em x. Inversamente, dado um número positivo y, a fórmula diz que se primeiro tirarmos o logaritmo e depois elevarmos a esta potência, temos de volta y.[86] Logo, as duas maneiras possíveis de combinar logaritmos e exponenciação dão o número original. Portanto, a função f(x) = logbx é a função inversa de f(x) = bx.[87]
As funções inversas estão estreitamente relacionadas às funções originais. Seus gráficos são correspondentes, apenas trocando-se o eixo das abcissas com o eixo das ordenadas (ou pela reflexão em relação à diagonal x = y), como mostrado nos gráficos ao lado: um ponto (t, u = bt) em um gráfico representa o ponto (u, t = logbu) no outro gráfico, pelo processo da reflexão, e vice-versa.[88] Consequentemente, logb(x) tende para o infinito se x cresce para o infinito, desde que b seja maior que um (nesse caso, logb(x) é uma função crescente). Para b < 1, logb(x) tende para menos infinito.[89]
Derivada e integral[editar | editar código-fonte]

As propriedades analíticas das funções passam para suas funções inversas. Então, como f(x) = bx é uma função diferenciável e contínua, logb(y) também é. Grosso modo, uma função contínua é diferenciável se seu gráfico não tiver "ângulos". Além disso, como a derivada de f(x) calcula a ln(b)bx pelas propriedades da função exponencial, a regra da cadeia implica que a derivada de logb(x) é dada por[82][90]
Isto é, a inclinação de uma tangente que toca o gráfico do logaritmo na base b no ponto (x, logb(x)) é igual a 1/(x ln(b)).[91] Em particular, a derivada de ln(x) é 1/x, o que implica que a integral de 1/x é ln(x) + C. A derivada, com uma definição generalizada, de f(x) é[92]
O quociente do gráfico à direita é chamado de derivada logarítmica de f. O cálculo de f'(x) por meio da derivada de ln(f(x)) é conhecido como diferenciação logarítmica.[93] Fórmulas relacionadas, tais como integrais de logaritmos para outras bases, podem ser derivadas a partir da equação abaixo usando a mudança de base. Portanto, a integral de um logaritmo natural ln(x) éː[94][95]
Representação da integral do logaritmo natural[editar | editar código-fonte]

O logaritmo natural de t corresponde à integral de 1/x dx de 1 para t:[97]
Em outras palavras, ln(t) é igual à área entre o eixo das abcissas e o gráfico da função 1/x, variando de x = 1 a x = t, tal como na figura ao lado. Esta é uma consequência do teorema fundamental do cálculo e do fato de que a derivada de ln(x) é 1/x. As fórmulas do logaritmo de produtos e potências podem ser derivadas a partir dessa definição (utilizando como exemplo, ln(tu) = ln(t) + ln(u)):[98]
A igualdade (1) divide a integral em duas partes, enquanto a igualdade (2) mostra a mudança de variável (w = x/t). Na ilustração abaixo, o desdobramento corresponde à divisão da área nas partes amarela e azul. Redimensionando a área azul do gráfico à esquerda no eixo das ordenadas e diminuindo-o no eixo das abcissas pelo mesmo fator t, conclui-se que seu tamanho é constante; dessa forma, movendo-o apropriadamente para o gráfico à direita, percebe-se a mesma área em proporções diferentes.[99]

A fórmula da potência ln(tr) = r ln(t) pode ser derivada de maneira semelhante, na qual a segunda igualdade usa uma mudança de variáveis (integração por substituição), w = x1/r:[100]
A soma dos recíprocos dos números naturais, é chamada de série harmônica.[101] Ela está intimamente relacionada ao logaritmo natural: quando n tende ao infinito, a diferença converge para um número conhecido como constante de Euler-Mascheroni. Esta relação auxilia na análise do desempenho de algoritmos tais como os conhecidos como quicksort.[102]
Existe também outra representação da integral de logaritmos que é usada em algumas situações:[103]
Isto pode ser verificado demonstrando-se que ele possui o mesmo valor para x=1, e a mesma derivada.
Transcendência do logaritmo[editar | editar código-fonte]
Todos os números reais que não são números algébricos são chamados de números transcendentes;[104] por exemplo, o π e o número de Euler são números deste tipo, porém não é. Quase todos os números reais são números transcendentais. O logaritmo é um exemplo de uma função transcendental. O Teorema de Gelfond-Schneider afirma que os logaritmos geralmente assumem valores transcendentais, isto é, "difíceis".[105]
Cálculo[editar | editar código-fonte]
Logaritmos são uma alternativa fácil de resolver cálculos em alguns casos, por exemplo, log10(1000) = 3. Geralmente, os logaritmos podem ser calculados usando a série de potências ou a média aritmética-geométrica, ou serem retirados de uma tabela de logaritmos pré-calculada, a qual oferece uma precisão definida.[106][107] O método de Newton, desenvolvido para resolver equações de forma iterativa de maneira aproximada, também pode ser usado para calcular o logaritmo, porque sua função inversa,[108] a função exponencial, é calculada de maneira eficiente por esse método. Usando tabelas de consulta, métodos como o algoritmo de Volder podem ser usados para cálculo de logaritmos se as únicas operações disponíveis são a adição e o deslocamento aritmético.[109] Além disso, o algoritmo do logaritmo binário calcula o lb(x) pela recursividade, baseada em repetidas potências de 2 de x, a partir da seguinte equação:[109]
Série de potências[editar | editar código-fonte]
Série de Taylor[editar | editar código-fonte]

Para qualquer número real z que satisfaça 0 < z < 2, a seguinte fórmula se aplica:[110]
Esta é uma forma para dizer que ln(z) pode ser aproximado a um valor cada vez mais preciso a partir da seguinte expressão:[111]
Por exemplo, com z = 1,5, a terceira aproximação equivale a 0,4167, que é cerca de 0,011 maior que a ln(1,5) = 0,405465.[112] Essa série proporciona uma aproximação de ln(z) com uma precisão arbitrária desde que o número de parcelas seja suficiente. Em cálculo elementar, ln(z) é, consequentemente, o limite desta série. Isto representa a série de Taylor do logaritmo natural para z = 1; a série de Taylor de ln z fornece uma aproximação útil para ln(1+z), quando z é pequeno, |z| < 1, logo[113]
Séries mais eficientes[editar | editar código-fonte]
Outra série para aproximação e resolução de cálculos logarítmicos é baseada na tangente hiperbólica inversa:[110]
Esta fórmula vale para qualquer valor real z > 0. Utilizando a notação sigma, ela também pode ser escrita de outro modo:[114]
Tal série pode ser derivada a partir da série de Taylor. Ela converge mais rapidamente que a série de Taylor, especialmente se z está próximo de 1.[115] Por exemplo, para z = 1,5, os três primeiros termos da segunda série aproximam ln(1,5) com um erro de cerca de 3×10−6. A rápida convergência de z próximo a 1 pode ser aproveitada da seguinte maneira: dada uma aproximação com baixa precisão y ≈ ln(z) e colocando , o logaritmo de z é:[116]
Quanto melhor a aproximação inicial y, mais próximo A será de 1, de modo que seu logaritmo pode ser calculado de maneira mais eficiente. A pode ser calculado utilizando a série exponencial, que converge rapidamente, desde que y não seja muito grande.[117] Para se calcular o logaritmo de um valores maiores de z, pode-se reduzir seu valor, escrevendo z = a · 10b, de modo que ln(z) = ln(a) + b · ln(10).[118]
Um método intimamente relacionado pode ser usado para calcular o logaritmo de números inteiros. A partir da série acima, conclui-se que:[119]
Se o logaritmo de um inteiro n com valor alto é conhecido, então esta série produz uma série de rápida convergência para log(n+1).[120]
Média aritmética-geométrica[editar | editar código-fonte]
A média aritmética-geométrica produz aproximações de alta precisão do logaritmo natural. ln(x) é aproximada com uma precisão de 2−p pela seguinte fórmula criada por Carl Friedrich Gauss:[121][122]
Nessa equação, M(x,y) representa a média aritmética-geométrica de x e y. Ela é obtida calculando-se repetidamente (x+y)/2 (média aritmética) e sqrt{(x*y)} (média geométrica), e depois fazendo com esses resultados sejam os próximos x e y. Esses números convergem rapidamente para um limite comum que é o valor de M(x,y). O valor de m é escolhido de tal modo que[123]
para garantir a precisão requerida. Um m maior faz com que o cálculo de M(x,y) requeira mais passos (os valores iniciais de x e y estão mais afastados, logo são necessários mais passos para convergir), mas dá maior precisão. As constantes π e ln(2) podem ser calculadas com séries de rápida convergência.[124]
Aplicações[editar | editar código-fonte]

Os logaritmos têm muitas aplicações dentro e fora da matemática. Algumas destas utilizações são relacionadas à noção de invariância de escala. Por exemplo, cada câmara da casca de um Nautilidae é uma cópia aproximada da seguinte, numa escala com um fator constante, dando origem à formação de uma espiral logarítmica.[125]
A lei de Benford que mostra a frequência da distribuição dos dígitos em fontes de dados também pode ser explicada pela invariância de escala.[126] Os logaritmos também estão vinculados à autossimilaridade. Por exemplo, aparecem na análise dos algoritmos que resolvem um problema por meio de sua divisão em dois problemas similares menores e, em seguida, a união de suas soluções.[127] As dimensões de formas geométricas autossimilares, isto é, figuras cujas partes se assemelham ao todo, também são baseadas em logaritmos. As escalas logarítmicas são convenientes para quantificar a variação relativa de um valor em oposição à sua diferença absoluta. Além disso, como a função logarítmica log(x) cresce bem lentamente para grandes valores de x, as escalas logarítmicas são usadas para compactar dados científicos em larga escala. Também são encontrados em muitas fórmulas científicas, tais como a equação de foguete de Tsiolkovsky, a equação de Fenske ou a equação de Nernst.[128]
Escalas logarítmicas[editar | editar código-fonte]

Quantidades científicas são muitas vezes expressas como logaritmos de outras quantidades, usando a escala logarítmica. Por exemplo, o decibel é uma unidade de medida associada a um nível de escala logarítmica. Baseia-se em uma razão de um logaritmo comum — 10 vezes o logaritmo comum de uma razão de potência ou 20 vezes o logaritmo comum de uma razão de tensão. Ele é utilizado para quantificar a perda de níveis de tensão em uma transmissão de sinais elétricos,[129] para descrever níveis de potência de sons em acústica[130] e a absorbância de luz no campo da espectrometria e óptica. A relação sinal-ruído que descreve a quantidade de ruído indesejado em relação a um sinal significativo também é medida em decibéis.[131] De forma similar, a relação sinal-ruído de pico é vulgarmente usada para avaliar a qualidade de som e métodos de compressão de imagens com base em logaritmos.[132]
A força de um terremoto é medida por um cálculo envolvendo o logaritmo comum da energia emitida pelo sismo; esse processo é feito pela escala Richter ou pela escala de magnitude de momento. Por exemplo, um terremoto de magnitude 5,0 gera 32 vezes (101.5) mais energia do que a produzida por um terremoto de magnitude 4,0, e um de 6,0 produz energia 1 000 vezes maior (103) do que o de magnitude 4,0.[133] Outra escala logarítmica é a de magnitude aparente, que mede a luminosidade de um corpo celeste a partir da razão entre o seu brilho e o de uma estrela de referência.[134] Outro exemplo é o pH na química: ele é definido como o logaritmo comum negativo da concentração de íons de hidrônio (H3O+) dissociados em solução aquosa. A atividade de íons de hidrônio em água neutra é 10−7 mol·L−1, logo um pH de 7. O vinagre tipicamente tem um pH de aproximadamente 3. A diferença de 4 corresponde a uma razão de 104 na atividade, isto é, a atividade do íon de hidrônio do vinagre é cerca de 10−3 mol·L−1.
Os gráficos semi-log, também chamados de papeis gráficos especiais, utilizam o conceito de escala logarítmica para visualização: um eixo, geralmente o das ordenadas, está em escala logarítmica. Por exemplo, o gráfico à direita comprime o aumento acentuado de 1 milhão a 1 trilhão no mesmo espaço (no eixo vertical) que o aumento de 1 a 1 milhão. Nesses gráficos, a função exponencial da forma f(x) = a · bx aparece com uma linha reta de declive igual ao logaritmo de b. Os gráficos log-log, também chamados de papel gráfico di-log pelo Instituto Tecnológico de Aeronáutica,[135] são aqueles em que ambos os eixos estão representados pela escala logarítmica, fazendo com que a forma f(x) = a · xk seja descrita como uma linha reta de declive igual ao expoente k. Isto se aplica na visualização e análise das leis de potência.[126]
Psicologia[editar | editar código-fonte]
Os logaritmos estão incluídos em diversas leis que descrevem a percepção humana.[136][137] A lei de Hick propõe uma relação logarítmica entre o tempo para os indivíduos escolherem uma alternativa e o número de opções que eles possuem para decidir.[138] A lei de Fitts, por outro lado, prevê que o tempo necessário para mover-se rapidamente de uma posição inicial até uma zona de destino final é uma função logarítmica da distância e da área do destino.[139] Na psicofísica, a lei de Weber-Fechner propõe uma relação logarítmica entre estímulo e sensação, tal como o peso real e o percebido de um item que uma pessoa está carregando.[140] Esta lei, entretanto, é menos precisa do que modelos mais recentes, tal como a lei potencial de Stevens.[141]
Estudos psicológicos concluíram que indivíduos com baixa aprendizagem em matemática tendem a estimar valores e resultados de maneira logarítmica, isto é, eles posicionam um número em uma linha imaginária de acordo com o seu logaritmo, de modo que 10 é posicionado tão próximo de 100 quanto 100 de 1 000. Com o aumento do ensino, essa estimativa se torna mais linear em algumas circunstâncias (posicionando 1 000 dez vezes mais distante), enquanto os logaritmos são usados quando os números a serem posicionados são difíceis de serem plotados linearmente.[142][143]
Teoria da probabilidade e estatística[editar | editar código-fonte]

Os logaritmos surgem na teoria das probabilidades: a lei dos grandes números indica que, para uma moeda honesta, quando o número de lançamentos da moeda tende para infinito, a proporção observada de caras se aproxima da metade. As oscilações dessa proporção em torno da metade são descritas pela lei do logaritmo iterado.[144]

Os logaritmos também ocorrem na distribuição log-normal: quando o logaritmo de uma variável aleatória tem uma distribuição normal, diz-se que a variável tem uma distribuição log-normal.[145] As distribuições log-normais são encontradas em muitos campos, sempre que uma variável seja formada pelo produto de muitas variáveis aleatórias positivas e independentes, por exemplo, no estudo da turbulência.[146]
Os logaritmos são usados para a estimativa de máxima probabilidade de modelos estatísticos paramétricos: para determinado modelo, a função de probabilidade depende de pelo menos um parâmetro que deve ser estimado. O valor máximo da função de probabilidade ocorre para o mesmo valor do parâmetro em que é máximo o logaritmo das probabilidades (o log-probabilidade ), porque o logaritmo é uma função crescente. O log-probabilidade é mais fácil para maximizar, especialmente para a multiplicação das probabilidades de variáveis aleatórias independentes.[147]
A lei de Benford descreve a ocorrência de dígitos em muitos conjuntos de dados, tal como as alturas de edifícios. De acordo com essa lei, a probabilidade de que o primeiro dígito decimal seja d (de 1 a 9) é igual a log10(d + 1) − log10(d), independentemente da unidade de medida.[148] Então, cerca de 30% dos dados podem ter 1 como o primeiro dígito, 18% de ser 2, e assim por diante.[149] Auditores examinam desvios em relação à lei de Benford para detectar fraudes contábeis.
Complexidade computacional[editar | editar código-fonte]
A análise de algoritmos é um ramo da ciência da computação que estuda o desempenho dos algoritmos (programas de computador que resolvem um determinado problema). Os logaritmos são valiosos para descrever algoritmos que dividem um problema em partes menores e juntam as soluções dos subproblemas.[150]
Por exemplo, para encontrar um número em uma lista ordenada, a pesquisa binária verifica a entrada do meio e trabalha com a metade antes ou depois da entrada do meio, se o número ainda não foi encontrado. Este algoritmo exige, em média, log2(N) comparações, onde N é o tamanho da lista. Similarmente, a ordenação por mistura (merge sort) classifica uma lista dividindo-a em duas metades e a classifica antes de ordenar os resultados. Esses algoritmos normalmente requerem um tempo aproximadamente proporcional a N · log(N).[151] A base desse logaritmo não é especificada, porque o resultado somente é alterado por um fator constante quando se utiliza uma outra base. Um fator constante é usualmente desconsiderado na análise de algoritmos sob o modelo de custo uniforme padrão.[152]
Diz-se que uma função f(x) cresce de modo logarítmico se f(x) é (exatamente ou aproximadamente) proporcional ao logaritmo de x (entretanto, descrições biológicas do crescimento de organismos usam este termo para uma função exponencial).[153] Por exemplo, qualquer número natural N pode ser representado no sistema de numeração binário com não mais do que log2(N) + 1 bits. Em outras palavras, a quantidade de memória para armazenar N cresce de modo logarítmico com N.
Entropia e caos[editar | editar código-fonte]

A entropia é uma medida da desordem de algum sistema. Na termodinâmica estatística, a entropia S de um sistema físico é definida como:[154]
O somatório é sobre todos os possíveis estados i do sistema em questão, tais como as posições das partículas de gás em um recipiente. Além disso, pi é a probabilidade de que o estado i seja atingido e k é a constante de Boltzmann. Similarmente, a entropia da informação mede a quantidade de informação: se um destinatário de mensagem pode esperar qualquer uma das possíveis mensagens com probabilidades iguais, então a informação transportada por qualquer mensagem é quantificada por log2(N) bits.[155]
O expoente de Lyapunov usa o logaritmo para aferir o grau de caotização de um sistema dinâmico. Por exemplo, para partículas movendo-se sobre uma mesa de bilhar oval, até mesmo pequenas mudanças nas condições iniciais resultam em caminhos muito diferentes da partícula. Tais sistemas são caóticos de maneira determinística, porque erros pequenos nas medições do estado inicial previsivelmente conduzem para estados finais muito diferentes.[156] Pelo menos um expoente de Lyapunov deterministicamente caótico é positivo.
Fractais[editar | editar código-fonte]

Os logaritmos são aplicados nas definições das dimensões dos fractais.[157] Fractais são objetos geométricos que são autossimilares: pequenas partes repetem, pelo menos aproximadamente, toda a estrutura global. O triângulo de Sierpinski (imagem) pode ser construído com três cópias dele mesmo, cada pedaço tendo metade da dimensão original. Isto faz com que a dimensão de Hausdorff desta estrutura seja log(3)/log(2) ≈ 1,58. Outra noção de dimensão baseada nos logaritmos é obtida pela contagem do número de caixas (Dimensão de Minkowski–Bouligand) necessário para cobrir o fractal em questão.[158]
Música[editar | editar código-fonte]
Os logaritmos estão relacionados aos tons e intervalos musicais. Em temperamento igual, a razão das frequências depende exclusivamente do intervalo entre dois tons, e não da frequência específica (ou altura) dos tons individuais. Por exemplo, a nota musical Lá tem uma frequência de 440 Hz e o Si bemol tem uma frequência de 466 Hz. O intervalo entre o Lá e o Si bemol é um semitom, assim como aquele entre o Si bemol e o Si (frequência de 493 Hz).[159]
Da mesma forma, a razão entre as frequências coincide:[160]
Portanto, os logaritmos podem ser utilizados para descrever os intervalos: um intervalo é medido em semitons tomando-se o logaritmo na base-21/12 da razão das frequências, enquanto o logaritmo na base-21/1200 da razão de frequências expressa o intervalo em cents, centésimo de um semitom. Este último é utilizado para codificação fina, como é necessário em temperamentos desiguais.[161]
| Intervalo (os dois tons são ouvidos ao mesmo tempo) |
Tom 72 ⓘ | Semitom ⓘ | Terça maior exata ⓘ | Terça maior ⓘ | Trítono ⓘ | Oitava ⓘ |
| Razão de frequências r | ||||||
| '’'Número correspondente de semitons |
||||||
| Número correspondente de cents |
Teoria dos números[editar | editar código-fonte]
Os logaritmos naturais estão estreitamente interligados com a função de contagem de números primos (2, 3, 5, 7, 11, ...), um tópico importante da teoria dos números. Para qualquer número inteiro x, a quantidade de números primos menores ou iguais a x é denotada pela constante π(x). O teorema dos números primos afirma que o π(x) é dado aproximadamente por:
no sentido em que a razão entre π(x) e aquela fração aproxima-se de 1 quando x tende ao infinito.[162] Como consequência, a probabilidade de que um número aleatoriamente escolhido entre 1 e x seja primo é inversamente proporcional ao número de dígitos decimais de x. Uma estimativa muito melhor de π(x) é dada pela função logaritmo integral Li(x), definida por:
A hipótese de Riemann, uma das mais antigas conjecturas matemáticas abertas, pode ser estabelecida em termos comparativos de π(x) e Li(x).[163] O teorema de Erdős–Kac descrevendo o número de fatores primos distintos também envolve os logaritmos naturais.
O logaritmo den fatorial, n! = 1 · 2 · ... · n, é dado por:
Este número pode ser utilizado para obter a fórmula de Stirling, uma aproximação do número n! para valores altos de n.[164]
Generalizações[editar | editar código-fonte]
Logaritmos complexos[editar | editar código-fonte]

Os números complexos a que resolvem a equação
são chamados de logaritmos complexos. Aqui, z é um número complexo. Um número complexo é geralmente representado como z = x + iy, onde x e y são números reais e o i é a unidade imaginária. Um número destes pode ser visualizado como um ponto em um plano complexo, como apresentado à direita.[165] A forma polar codifica um número complexo não-nulo z por seu valor absoluto, que é a distância r da origem e um ângulo entre o eixo x e a linha que passa entre a origem e z. Este ângulo é chamado de argumento de z. O valor absoluto r de z é[166]
O argumento não é exclusivamente especificado por z: ambos os ângulos φ e φ' = φ + 2π são argumentos de z, porque adicionarem-se 2π radianos ou 360 graus ao ângulo φ corresponde ao "enrolamento" sobre a origem no sentido anti-horário em uma volta. O número complexo resultante é novamente z, como ilustrado na figura à direita. Entretanto, exatamente um argumento φ satisfaz a condição de: −π < φ e φ ≤ π. Ele é chamado de argumento principal, denotado Arg(z), com A maiúsculo[167] (uma normalização alternativa é 0 ≤ Arg(z) < 2π.[168])

Utilizando-se as funções trigonométricas seno e cosseno, ou a exponencial complexa, respectivamente, r e φ são tais que as seguintes identidades se aplicam:[170]
Isto implica que a a-ésima potência de e é igual a z, onde
φ é o argumento principal Arg(z) e n é um inteiro arbitrário. Qualquer a é chamado de um logaritmo complexo de z. Há uma quantidade infinita deles, em contraste com os logaritmos reais, que são únicos. Se n = 0, a é chamado de valor principal do logaritmo, denotado Log(z). O argumento principal de qualquer número real positivo x é 0; logo Log(x) é um número real e é igual ao logaritmo real natural. Logo, as fórmulas acima dos logaritmos de produtos e potências não são generalizadas como o valor principal de um logaritmo complexo.[171]
A ilustração da direita descreve o Log(z). A descontinuidade, isto é, o salto no matiz na parte negativa do eixo x, é causada pelo salto do argumento principal ali. Este lugar geométrico é chamado de ponto de ramificação. Este comportamento só pode ser contornado pela restrição da extensão do ângulo φ. Então o argumento de z e, consequentemente, seu logaritmo se tornam funções multivaloradas.[172]
Inversos de outras funções exponenciais[editar | editar código-fonte]
A exponenciação ocorre em muitas áreas da matemática e sua função inversa é muitas vezes referida como o logaritmo. Por exemplo, o logaritmo de uma matriz é a função inversa da exponencial matricial.[173] Outro exemplo é a função logarítmica p-adic, cujo inverso é a função exponencial p-adic. Ambas são definidas através da série de Taylor para o caso real.[174] No contexto da geometria diferencial, o mapa exponencial traça o espaço tangente em um ponto de uma variável na vizinhança deste ponto. O seu inverso também é chamado o mapa logarítmico.[175]
No contexto de grupos finitos, a exponenciação é dada pela multiplicação repetida de um elemento b do grupo com ele mesmo. O logaritmo discreto é o inteiro n que resolve a equação bn = x, onde x é um elemento do grupo. A exponenciação pode ser realizada de forma eficiente, mas em alguns casos o logaritmo discreto é muito difícil de ser calculado. Esta assimetria tem aplicação importante na criptografia de chave pública, como, por exemplo, a troca de chaves de Diffie-Hellman, uma rotina que permite a troca de chaves criptográficas dentro de canais de comunicação inseguros.[176] O logaritmo de Zech está relacionado com o logaritmo discreto no grupo multiplicativo de elementos diferentes de zero de um corpo finito.[177]
Outras funções inversas do tipo do logaritmo incluem o logaritmo duplo ln(ln(x)), o super ou hiper-4-logaritmo (uma ligeira variação do qual é o chamado logaritmo iterado na ciência da computação), a função W de Lambert e o logit. Eles são as funções inversas da função exponencial dupla, da tetração, de f(w) = wew[178] e da função logística, respectivamente.[179]
Conceitos relacionados[editar | editar código-fonte]
Na perspectiva da matemática pura, a identidade log(cd) = log(c) + log(d) expressa um grupo isomórfico entre os números reais positivos sob a multiplicação e os reais sob a adição. As funções logarítmicas são os únicos isomorfismos contínuos entre estes grupos.[180] Por este isomorfismo, a medida de Haar (Medida de Lebesgue) dx nos números reais corresponde à medida de Haar dx/x nos números reais positivos.[181] Na análise complexa e na geometria algébrica, as formas diferenciais da forma df/f são conhecidas como formas com polos logarítmicos.[182]
O polilogaritmo é a função definida por:
Ele está relacionado aos logaritmos naturais pela Li1(z) = −ln(1 − z). Além disso, Lis(1) é igual à função zeta de Riemann ζ(s).[183]
Ver também[editar | editar código-fonte]
Referências
- ↑ «Confira este exemplo e faça outros com O Monitor». omonitor.io. Consultado em 25 de março de 2016
- ↑ «Banco de imagens — Volume 1». Portal Matemática. Editora Saraiva. Consultado em 1 de dezembro de 2014. Arquivado do original em 10 de dezembro de 2015
- ↑ «1º Exame de Classificação». Revista Eletrônica. Universidade Estadual do Rio de Janeiro. Consultado em 3 de dezembro de 2014
- ↑ Barroso, Juliane Matsubara. Conexões com a Matemática. [S.l.]: Editora Moderna. 798 páginas. ISBN 9788516082291. Consultado em 2 de dezembro de 2014
- ↑ Clark, Kathleen. «Logarithms. The early history of a familiar function». MAA. Consultado em 2 de dezembro de 2014
- ↑ Função matemática. enciclopédia da matemática 3ª ed. Moscou: Grande Enciclopédia da Rússia. 1982
- ↑ «Pré Cálculo» (PDF). Andrade, Rubens Leão. Universidade Federal de Tocantins. Consultado em 3 de dezembro de 2014. Arquivado do original (PDF) em 8 de dezembro de 2014
- ↑ «Logaritmo e Exponencial» (PDF). Universidade Federal de Minas Gerais. Consultado em 3 de dezembro de 2014[ligação inativa]
- ↑ Smith, Steven (2013). Digital Signal Processing: A Practical Guide for Engineers and Scientists. [S.l.]: Newnes. 672 páginas. ISBN 9780080477329
- ↑ «Acadêmicos "ocupam" UEAP na semana universitária». Universidade Estadual do Amapá. Consultado em 3 de dezembro de 2014
- ↑ Brown, Clifford (2010). Fractal Analysis. [S.l.]: Sage. p. 19. 112 páginas. ISBN 9781483343129
- ↑ Royal Military Academy (2007). Arithmetic, algebra, differential and integral calculus. [S.l.]: Harvard University Press. p. 183
- ↑ Paul Garrett; Daniel Lieman (2005). Public-key Cryptography. [S.l.]: American Mathematical Society Short Course. p. 91. 183 páginas. ISBN 9780821867679
- ↑ Miller, Jeff. «Earliest known uses of some of the words of Mathematics (L)». Consultado em 29 de agosto de 2009
- ↑ Soares, Evanildo Costa. «Uma investigação história sobre os logaritmos com sugestão didática». Centro de ciências exatas da Terra. Universidade Federal do Rio Grande do Norte. Consultado em 3 de dezembro de 2014[ligação inativa]
- ↑ «Aplicações da Informática no Ensino da Matemática». Universidade Federal da Grande Dourados. Consultado em 3 de dezembro de 2014
- ↑ dos Santos, João Carlos. Matematica Financeira I. com a Calculadora Hp 12c. São Paulo: Villipress. p. 62. 121 páginas. ISBN 9788574730448. Consultado em 3 de dezembro de 2014
- ↑ Caramelo, José Amado. Biomatemática. Uma introdução para o curso da matemática 2ª ed. Coimbra: Imprensa da Universidade de Coimbra. p. 30. 430 páginas. ISBN 9789728704230. Consultado em 3 de dezembro de 2014
- ↑ Shirali, Shailesh (2002), A Primer on Logarithms, ISBN 978-81-7371-414-6, Hyderabad: Universities Press, esp. seção 2
- ↑ «Respostas Esperadas Oficias» (PDF). Universidade Federal de Goiás. 11 de setembro de 2009. Consultado em 3 de dezembro de 2014
- ↑ Kate, S.K.; Bhapkar, H.R. (2009). «1». Basics of Mathematics. Pune: Technical Publications. ISBN 978-81-8431-755-8
- ↑ «Bibliotecas: tópicos de destaque». Faculdade de Tecnologia e Ciências Exatas. Universidade São Judas Tadeu. Consultado em 3 de dezembro de 2014
- ↑ Sanches, Paulo Sérgio Bedaque. Matematikōs. São Paulo: Editora Saraiva. 480 páginas. ISBN 9788502101951. Consultado em 2 de dezembro de 2014
- ↑ «Programa de disciplina física». Departamento de Física. Universidade Federal de Roraima. Consultado em 3 de dezembro de 2014
- ↑ Mayorga, Rodrigo (9 de janeiro de 2007). «Análise de transmissão de preços do mercado atacadista de melão do Brasil». Revista de Economia e Sociologia Rural. Scielo. Consultado em 3 de dezembro de 2014
- ↑ Rodrigues, Aldo. Funções Analíticas com Aplicações 1ª ed. Rio de Janeiro: Editora Livraria da Fisica. p. 45. 210 páginas. ISBN 9788588325531. Consultado em 3 de dezembro de 2014
- ↑ Shailesh Shirali 2002, seção 4, (Douglas Downing 2003, p. 275) e Kate & Bhapkar 2009, p. 1-1
- ↑ «Une histoire des logarithmes» (PDF). Université Libre de Bruxelles. Consultado em 2 de dezembro de 2014
- ↑ Paiva, Manoel (2010). Matemática Paiva 5ª ed. São Paulo: Atual Editora. p. 280. 422 páginas. ISBN 9788516068301. Consultado em 2 de dezembro de 2014
- ↑ Roseveare, David (2004). Trigonometry. Washington: Hemus. p. 51. 260 páginas. ISBN 8528903990. Consultado em 3 de dezembro de 2014 [ligação inativa]
- ↑ Lopes, Maria Isabella. «Diagnóstico de alergia a baratas no ambiente clínico: estudo comparativo entre o teste cutâneo e IgE específica». Jornal de Pediatria. Scielo. Consultado em 3 de dezembro de 2014
- ↑ a b Napier, John (1616). A description of the admirable table of logarithms. Londres: Nikolas Okes. 31 páginas. Consultado em 2 de dezembro de 2014
- ↑ Bernstein, Stephen; Bernstein, Ruth (1999), Schaum's outline of theory and problems of elements of statistics. I, Descriptive statistics and probability, ISBN 978-0-07-005023-5, Schaum's outline series, Nova Iorque: McGraw-Hill, p. 21
- ↑ «Introduzindo o Conceito de Logaritmo com a Calculadora Científica» (PDF). EL Laureano. Spiem. 8 de outubro de 2008. Consultado em 3 de dezembro de 2014
- ↑ Garcia, Antonio Carlos (2008). Sequências. progressão aritmética, progressão geométrica e função logarítmica. [S.l.]: Clube de autores. p. 36. 58 páginas. Consultado em 3 de dezembro de 2014
- ↑ Downing, Douglas (2003), Algebra the Easy Way, ISBN 978-0-7641-1972-9, Barron's Educational Series, Hauppauge, N.Y.: Barron's, capítulo 17, p. 275
- ↑ Wegener, Ingo (2005), Complexity theory: exploring the limits of efficient algorithms, ISBN 978-3-540-21045-0, Berlim, Nova Iorque: Springer-Verlag, p. 20
- ↑ Van der Lubbe, Jan C. A. (1997), Information Theory, ISBN 9780521467605, Cambridge University Press, p. 3
- ↑ Allen, Elizabeth; Triantaphillidou, Sophie (2011), The Manual of Photography, ISBN 9780240520377, Taylor & Francis, p. 228
- ↑ B. N. Taylor (1995), Guide for the Use of the International System of Units (SI), US Department of Commerce, consultado em 21 de novembro de 2014, arquivado do original em 29 de junho de 2007
- ↑ Franz Embacher; Petra Oberhuemer, Mathematisches Lexikon (em alemão), Mathe online: für Schule, Fachhochschule, Universität unde Selbststudium, consultado em 22 de março de 2012
- ↑ Gullberg, Jan (1997), Mathematics: from the birth of numbers., ISBN 978-0-393-04002-9, Nova Iorque: W. W. Norton & Co
- ↑ Paul Halmos (1985), I Want to Be a Mathematician: An Automathography, ISBN 978-0-387-96078-4, Berlim, Nova Iorque: Springer-Verlag
- ↑ Irving Stringham (1893), Uniplanar algebra: being part I of a propædeutic to the higher mathematical analysis, The Berkeley Press, p. 13
- ↑ Roy S. Freedman (2006), Introduction to Financial Technology, ISBN 978-0-12-370478-8, Amsterdã: Academic Press, p. 59
- ↑ McFarland, David (2007), Quarter Tables Revisited: Earlier Tables, Division of Labor in Table Construction, and Later Implementations in Analog Computers, p. 1
- ↑ Robson, Eleanor (2008). Mathematics in Ancient Iraq: A Social History. [S.l.: s.n.] p. 227. ISBN 978-0691091822
- ↑ Grande enciclopédia portuguesa e brasileira. Ilustrada com cerca de 15000 gravuras e 400 estampas a cores. Universidade de Michigan: Editorial Enciclopédia. 2007. p. 383-385. Consultado em 3 de dezembro de 2014
- ↑ Gupta, R. C. (2000), «History of Mathematics in India», in: Hoiberg, Dale; Ramchandani, Indu, Students' Britannica India: Select essays, Popular Prakashan, p. 329
- ↑ Stifelio, Michaele (1544), Arithmetica Integra, Nuremberg: Iohan Petreium
- ↑ Bukhshtab, A.A.; Pechaev, V.I. (2001), «Arithmetic», in: Hazewinkel, Michiel, Enciclopédia de Matemática, ISBN 978-1-55608-010-4 (em inglês), Springer
- ↑ Vivian Shaw Groza; Susanne M. Shelley (1972), Precalculus mathematics, ISBN 978-0-03-077670-0, Nova Iorque: Holt, Rinehart and Winston, p. 182
- ↑ Napier, John (1614), Mirifici Logarithmorum Canonis Descriptio [The Description of the Wonderful Rule of Logarithms] (em latim), Edinburgh, Scotland: Andrew Hart
- ↑ Ernest William Hobson (1914), John Napier and the invention of logarithms, 1614, Cambridge: The University Press
- ↑ a b Gladstone-Millar, Lynne (2003), John Napier: Logarithm John, ISBN 978-1-901663-70-9, National Museums Of Scotland, p. 44
- ↑ Napier, Mark (1834), Memoirs of John Napier of Merchiston, Edinburgh: William Blackwood, p. 392.
- ↑ William Harrison De Puy (1893), The Encyclopædia Britannica: a dictionary of arts, sciences, and general literature ; the R.S. Peale reprint, 17 9.ª ed. , Werner Co., p. 179
- ↑ Maor, Eli (2009), e: The Story of a Number, ISBN 978-0-691-14134-3, Princeton University Press
- ↑ Em 1647, Grégoire de Saint-Vincent publicou seu livro, Opus geometricum quadraturae circuli et sectionum coni, vol. 2 (Antuérpia, (Bélgica): Johannes and Jakob Meursius, 1647). On page 586
- ↑ Alphonse Antonio de Sarasa, Solutio problematis a R.P. Marino Mersenne Minimo propositi … [Proposta de solução para um problema pelo reverendo padre Marin Mersenne, membro da ordem Minim … ], (Antuérpia, (Bélgica): Johannes e Jakob Meursius, 1649).
- ↑ J. J. O'Connor; E. F. Robertson (Setembro de 2001), The number e, The MacTutor History of Mathematics archive, consultado em 2 de fevereiro de 2009
- ↑ Cajori, Florian (1991), A History of Mathematics, ISBN 978-0-8218-2102-2 5ª ed. , Providence, RI: AMS Bookstore, p. 152
- ↑ «Confira este exemplo e faça outros com O Monitor». omonitor.io. Consultado em 25 de março de 2016
- ↑ a b Maor 2009, seções 1, 13
- ↑ Eves, Howard Whitley (1992), An introduction to the history of mathematics, ISBN 978-0-03-029558-4, The Saunders series 6ª ed. , Philadelphia: Saunders
- ↑ Boyer, Carl B. (1991), A History of Mathematics, ISBN 978-0-471-54397-8, Nova Iorque: John Wiley & Sons, p. 484, 489
- ↑ Santos, Fátima; Rosane J. B. «Crescimento alométrico em crianças eutróficas e desnutridas». Biblioteca Virtual em Saúde. Bireme. Consultado em 3 de dezembro de 2014
- ↑ Bryant, Walter W., A History of Astronomy, Londres: Methuen & Co, p. 44
- ↑ Campbell-Kelly, Martin (2003), The history of mathematical tables: from Sumer to spreadsheets, ISBN 978-0-19-850841-0, Oxford scholarship online, Oxford University Press, seção 2
- ↑ Abramowitz, Milton; Stegun, Irene A., eds. (1972), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, ISBN 978-0-486-61272-0 10ª ed. , Nova Iorque: Dover Publications, seção 4.7., p. 89
- ↑ de Oliveira, Evangelina X. G. «Acesso à internação hospitalar nos municípios brasileiros em 2000: territórios do Sistema Único de Saúde». Scielo SP. Consultado em 3 de dezembro de 2014
- ↑ «Quantificação da biomassa acima do solo de Acacia mearnsii». Cascavel. Universidade Federal de Santa Maria. Consultado em 3 de dezembro de 2014
- ↑ Spiegel, Murray R.; Moyer, R.E. (2006), Schaum's outline of college algebra, ISBN 978-0-07-145227-4, Schaum's outline series, Nova Iorque: McGraw-Hill, p. 264
- ↑ Bails, Benito (2009). Tabla de logaritmos de todos los números naturales desde 1 hasta 20000; y de todos los logaritmos de los senos, tangentes de todos los grados y minutos del quadrante del circulo. [S.l.]: Universidade Complutense de Madri. p. 1-425. 531 páginas. Consultado em 3 de dezembro de 2014
- ↑ Resende, André Lara. «Sobre as causas da recente aceleração inflacionária». Pesquisa e Planejamento Econômico. Consultado em 3 de dezembro de 2014
- ↑ Drago, Massimo (2005). Manuale per i concorsi di sottufficiale nell'esercito. Paris: Alpha Test. p. 292-294. 416 páginas. ISBN 9788848306201. Consultado em 3 de dezembro de 2014
- ↑ Schneider, Cristina (1986). «Padrões ecocardiográficos normais em crianças na cidade do Rio de Janeiro: I. Relaçäo entre medidas ecocardiográficas e padröes antropométricos». Bireme. Consultado em 3 de dezembro de 2014
- ↑ Devlin, Keith (2004). Sets, functions, and logic: an introduction to abstract mathematics. Col: Chapman & Hall/CRC mathematics 3ª ed. Boca Raton, Fla: Chapman & Hall/CRC. ISBN 1-58488-449-5
- ↑ Lang, Serge (1997), Undergraduate analysis, ISBN 978-0-387-94841-6, Undergraduate Texts in Mathematics 2nd ed. , Berlim, Nova Iorque: Springer-Verlag, MR 1476913, seção III.3
- ↑ Cueto, Maria José Vásquez. Curso interactivo de matemáticas básicas para ciencias. [S.l.]: Delta Publicaciones. p. 20-22. 127 páginas. ISBN 9788496477056. Consultado em 3 de dezembro de 2014
- ↑ «Inercia inflacionária e inflação inercial». Biblioteca Digital. Fundação Getúlio Vargas. Consultado em 3 de dezembro de 2014
- ↑ a b Lang 1997, seção IV.2
- ↑ Boucharlat, J. L. (1834). Elementos de cálculo diferencial y de cálculo integral. Madri: Imprenta Real. p. 42. 436 páginas. Consultado em 3 de dezembro de 2014
- ↑ Dieudonné, Jean (1969). Foundations of Modern Analysis. 1. [S.l.]: Academic Press. p. 84
- ↑ «e-Cálculo para propriedades matemáticas». Centro de Ensino e Pesquisa Aplicada. Universidade de São Paulo. 2 de março de 2012. Consultado em 23 de novembro de 2014
- ↑ «Artículo». Educar. Redalyc. 2011. Consultado em 3 de dezembro de 2014
- ↑ Stewart, James (2007), Single Variable Calculus: Early Transcendentals, ISBN 978-0-495-01169-9, Belmont: Thomson Brooks/Cole, seção 1.6
- ↑ «Consumo, digestibilidade, desempenho, composição corporal e exigências nutricionais de bezerros alimentados com dietas contendo diferentes níveis de volumoso..». Alianza de Servicios de Información Agraria. Universidade Federal de Viçosa. Consultado em 3 de dezembro de 2014
- ↑ Rocha, Carlos Henrique. «Complementaridade versus substituição entre investimento público e privado na economia brasileira: 1965-90». Revista Brasileira de Economia. Fundação Getúlio Vargas. Consultado em 3 de dezembro de 2014
- ↑ «Calculation of d/dx(Log(b,x))». Wolfram Alpha. Wolfram Research. Consultado em 15 de março de 2011
- ↑ Dailami, Mansoor (2003). Qualidade do crescimento a(t). [S.l.]: Universidade Estadual Paulista. p. 209. 304 páginas. ISBN 9788571394414. Consultado em 3 de dezembro de 2014
- ↑ Véras, Antonia Sherlânea Chaves (2001). «Composição corporal e requisitos líquidos e dietéticos de macroelementos minerais de bovinos nelore não-castrados» (PDF). Scielo. Consultado em 3 de dezembro de 2014
- ↑ Kline, Morris (1998), Calculus: an intuitive and physical approach, ISBN 978-0-486-40453-0, Dover books on mathematics, Nova Iorque: Dover Publications, p. 386
- ↑ «Confira este exemplo e faça outros com O Monitor». omonitor.io. Consultado em 25 de março de 2016
- ↑ «Calculation of Integrate(ln(x))». Wolfram Alpha. Wolfram Research. Consultado em 15 de março de 2011
- ↑ Abramowitz & Stegun, eds. 1972, p. 69
- ↑ Backes. «Composição corporal e exigências líquidas de energia e proteína para ganho de peso de novilhos santa gertrudis» (PDF). Revista Brasileira de Economia. Consultado em 3 de dezembro de 2014
- ↑ Courant, Richard (1988), Differential and integral calculus. Vol. I, ISBN 978-0-471-60842-4, Wiley Classics Library, Nova Iorque: John Wiley & Sons, MR 1009558, seção III.6
- ↑ Faraco, Mário Antonio (2008). «Seleção de modelos de variabilidade espacial para elaboração de mapas temáticos de atributos físicos do solo e produtividade da soja». Sidalc. Consultado em 3 de dezembro de 2014
- ↑ Ríos, Mario Alberto Gaviria (2005). Lecturas sobre Crecimiento Económico Regional. [S.l.]: Juan Carlos Martínez Coll. p. 132. ISBN 9788468942704. Consultado em 3 de dezembro de 2014
- ↑ Marroquín, Néstor (2010). Tras los pasos de un... Hacker. [S.l.]: NMC Research Cía Ltda. p. 659. 746 páginas. ISBN 9781453850435. Consultado em 3 de dezembro de 2014
- ↑ Havil, Julian (2003), Gamma: Exploring Euler's Constant, ISBN 978-0-691-09983-5, Princeton University Press, seções 11.5 e 13.8
- ↑ «Eletrólitos sólidos poliméricos à base de polissacarídeos: síntese e caracterização». AM Regiani. Universidade de São Paulo. 2000. Consultado em 3 de dezembro de 2014
- ↑ Nomizu, Katsumi (1996), Selected papers on number theory and algebraic geometry, ISBN 978-0-8218-0445-2, 172, Providence, RI: AMS Bookstore, p. 21
- ↑ Baker, Alan (1975), Transcendental number theory, ISBN 978-0-521-20461-3, Cambridge University Press, p. 10
- ↑ Muller, Jean-Michel (2006), Elementary functions, ISBN 978-0-8176-4372-0 2ª ed. , Boston, MA: Birkhäuser Boston, seções 4.2.2 (p. 72) e 5.5.2 (p. 95)
- ↑ Hart; Cheney; Lawson; et al. (1968), Computer Approximations, SIAM Series in Applied Mathematics, Nova Iorque: John Wiley, seção 6.3, p. 105–111
- ↑ Zhang, M.; Delgado-Frias, J.G.; Vassiliadis, S. (1994), «Table driven Newton scheme for high precision logarithm generation» (PDF), IEE Proceedings Computers & Digital Techniques, ISSN 1350-2387, 141 (5): 281–292, doi:10.1049/ip-cdt:19941268, consultado em 2 de dezembro de 2014, arquivado do original (PDF) em 9 de maio de 2012
- ↑ a b «Revisão de Geometria Plana» (PDF). Rumo à Oita. Instituto Militar de Engenharia. 1984. Consultado em 3 de dezembro de 2014. Arquivado do original (PDF) em 24 de setembro de 2015
- ↑ a b Abramowitz & Stegun, eds. 1972, p. 68
- ↑ Baptista, A. «Palestra sobre logaritmos» (PDF). Sober. Consultado em 3 de dezembro de 2014
- ↑ William D. Callister (2002). Introducción a la ciencia e ingeniería de los materiales, Volume 1. [S.l.]: Reverte. p. 308. 524 páginas. ISBN 9788429172539. Consultado em 3 de dezembro de 2014
- ↑ Salmazo, Leandara Oliveira. «Influência da adição de nanopartículas paramagnéticas de Ni0,5Zn0,5Fe2O4 nas propriedades estruturais e dielétricas de filmes de borracha natural: preparação e caracterização». Universidade Estadual Paulista. Consultado em 3 de dezembro de 2014
- ↑ Joshuah de Bragança Soares (2005). Dicionário de matemática. [S.l.]: Hemus. p. 121. 285 páginas. ISBN 9788528905526. Consultado em 3 de dezembro de 2014 [ligação inativa]
- ↑ Francisco Lombardi Neto. «Erosividade da chuva: sua distribuição e relação com as perdas de solo em Campinas (SP).». Scientific Electronic Library Online. Sidalc. Consultado em 3 de dezembro de 2014
- ↑ Lenimar Nunes de Andrade (Setembro de 2011). «Máxima: um completo programa de computação algébrica» (PDF). Universidade Federal do Paraíba. Consultado em 3 de dezembro de 2014. Arquivado do original (PDF) em 17 de abril de 2015
- ↑ Basic: introducción a la programación. [S.l.]: Reverte. 1984. p. 58. 271 páginas. ISBN 9788471462473. Consultado em 3 de dezembro de 2014
- ↑ Luiz Fernando Alves. «Clubes de convergência entre os municípios de Minas Gerais» (PDF). Universidade Federal de Minas Gerais. Consultado em 3 de dezembro de 2014 [ligação inativa][ligação inativa]
- ↑ Igor Viveiros Souza. «Eficiência do setor hospitalar nos municípios paulistas». Scielo. Consultado em 3 de dezembro de 2014
- ↑ Circuitos e dispositivos eletrônicos. [S.l.]: Hemus. p. 14. 98 páginas. ISBN 9788528900118. Consultado em 3 de dezembro de 2014 [ligação inativa]
- ↑ Sasaki, T.; Kanada, Y. (1982), «Practically fast multiple-precision evaluation of log(x)», Journal of Information Processing, 5 (4): 247–250, consultado em 30 de março de 2011
- ↑ Ahrendt, Timm (1999), Fast computations of the exponential function, Lecture notes in computer science, 1564, Berlim, Nova Iorque: Springer, pp. 302–312, doi:10.1007/3-540-49116-3_28
- ↑ Domingos Junqueira de Brito. Astros e Ostras. [S.l.]: Editora Agora. p. 313. 368 páginas. ISBN 9788571835399. Consultado em 3 de dezembro de 2014
- ↑ Ulisses dos Santos Borges. «Curso de Logaritmo para o Ensino Médio com proposta de atividades alternativas». Matemática em Rede Nacional. Consultado em 3 de dezembro de 2014. Arquivado do original em 18 de maio de 2015
- ↑ «As aplicações dos logaritmos nas ciências naturais por meio de resolução de problemas». Instituto Federal de Goiás. Consultado em 3 de dezembro de 2014
- ↑ a b «Bolzano e Laplace; O Teorema Fundamental das Curvas Planas e Aplicações». VI Enapetmat. Universidade Federal de Santa Catarina e Universidade de Brasília. Consultado em 3 de dezembro de 2014
- ↑ Ricciardi, Luigi M. (1990), Lectures in applied mathematics and informatics, ISBN 978-0-7190-2671-3, Manchester: Manchester University Press, p. 21, seção 1.3.2
- ↑ Jasmuheen (2008). O programa Prana. [S.l.]: Lulu.com. p. 63. 154 páginas. ISBN 9781409205258. Consultado em 3 de dezembro de 2014
- ↑ Bakshi, U. A. (2009), Telecommunication Engineering, ISBN 978-81-8431-725-1, Pune: Technical Publications, seção 5.2
- ↑ Maling, George C. (2007), «Noise», in: Rossing, Thomas D., Springer handbook of acoustics, ISBN 978-0-387-30446-5, Berlim, Nova Iorque: Springer-Verlag, seção 23.0.2
- ↑ Tashev, Ivan Jelev (2009), Sound Capture and Processing: Practical Approaches, ISBN 978-0-470-31983-3, Nova Iorque: John Wiley & Sons, p. 48
- ↑ Chui, C.K. (1997), Wavelets: a mathematical tool for signal processing, ISBN 978-0-89871-384-8, SIAM monographs on mathematical modeling and computation, Philadelphia: Society for Industrial and Applied Mathematics, p. 180
- ↑ Crauder, Bruce; Evans, Benny; Noell, Alan (2008), Functions and Change: A Modeling Approach to College Algebra, ISBN 978-0-547-15669-9 4° ed. , Boston: Cengage Learning, seção 4.4.
- ↑ Bradt, Hale (2004), Astronomy methods: a physical approach to astronomical observations, ISBN 978-0-521-53551-9, Cambridge Planetary Science, Cambridge University Press, seção 8.3, página 231
- ↑ «Papel logarítmico: este tipo de papel é utilizado para representar relações funcionais exponenciais entre duas grandezas». Instituto Tecnológico de Aeronáutica. Consultado em 24 de novembro de 2014. Arquivado do original em 10 de dezembro de 2014
- ↑ Goldstein, E. Bruce (2009), Encyclopedia of Perception, ISBN 978-1-4129-4081-8, Encyclopedia of Perception, Thousand Oaks, CA: Sage, p. 355–356
- ↑ Matthews, Gerald (2000), Human performance: cognition, stress, and individual differences, ISBN 978-0-415-04406-6, Human Performance: Cognition, Stress, and Individual Differences, Hove: Psychology Press, p. 48
- ↑ Welford, A. T. (1968), Fundamentals of skill, ISBN 978-0-416-03000-6, Londres: Methuen, OCLC 219156, p. 61
- ↑ Paul M. Fitts (Junho de 1954), «The information capacity of the human motor system in controlling the amplitude of movement», Journal of Experimental Psychology, 47 (6): 381–391, PMID 13174710, doi:10.1037/h0055392, reimpresso por Paul M. Fitts (1992), «The information capacity of the human motor system in controlling the amplitude of movement» (PDF), Journal of Experimental Psychology: General, 121 (3): 262–269, PMID 1402698, doi:10.1037/0096-3445.121.3.262, consultado em 30 de março de 2011
- ↑ Banerjee, J. C. (1994), Encyclopaedic dictionary of psychological terms, ISBN 978-81-85880-28-0, New Delhi: M.D. Publications, OCLC 33860167, p. 304
- ↑ Nadel, Lynn (2005), Encyclopedia of cognitive science, ISBN 978-0-470-01619-0, Nova Iorque: John Wiley & Sons
- ↑ Siegler, Robert S.; Opfer, John E. (2003), «The Development of Numerical Estimation. Evidence for Multiple Representations of Numerical Quantity» (PDF), Psychological Science, 14 (3): 237–43, PMID 12741747, doi:10.1111/1467-9280.02438, consultado em 2 de dezembro de 2014, cópia arquivada (PDF) em 17 de maio de 2011
- ↑ Dehaene, Stanislas; Izard, Véronique; Spelke, Elizabeth; Pica, Pierre (2008), «Log or Linear? Distinct Intuitions of the Number Scale in Western and Amazonian Indigene Cultures», Science, 320 (5880): 1217–1220, PMC 2610411
 , PMID 18511690, doi:10.1126/science.1156540
, PMID 18511690, doi:10.1126/science.1156540
- ↑ Breiman, Leo (1992), Probability, ISBN 978-0-89871-296-4, Classics in applied mathematics, Philadelphia: Society for Industrial and Applied Mathematics, seção 12.9
- ↑ Aitchison, J.; Brown, J. A. C. (1969), The lognormal distribution, ISBN 978-0-521-04011-2, Cambridge University Press, OCLC 301100935
- ↑ Jean Mathieu; Julian Scott (2000), An introduction to turbulent flow, ISBN 978-0-521-77538-0, Cambridge University Press, p. 50
- ↑ Rose, Colin; Smith, Murray D. (2002), Mathematical statistics with Mathematica, ISBN 978-0-387-95234-5, Springer texts in statistics, Berlim, Nova Iorque: Springer-Verlag, seção 11.3
- ↑ Tabachnikov, Serge (2005), Geometry and Billiards, ISBN 978-0-8218-3919-5, Providence, R.I.: American Mathematical Society, pp. 36–40, seção 2.1
- ↑ Durtschi, Cindy; Hillison, William; Pacini, Carl (2004), «The Effective Use of Benford's Law in Detecting Fraud in Accounting Data» (PDF), Journal of Forensic Accounting, V: 17–34, consultado em 2 de dezembro de 2014, arquivado do original (PDF) em 15 de abril de 2012
- ↑ Harel, David; Feldman, Yishai A. (2004), Algorithmics: the spirit of computing, ISBN 978-0-321-11784-7, Nova Iorque: Addison-Wesley, p. 143
- ↑ Donald Knuth 1998, seção 5.2.4, pp. 158–168
- ↑ Wegener, Ingo (2005), Complexity theory: exploring the limits of efficient algorithms, ISBN 978-3-540-21045-0, Berlim, Nova Iorque: Springer-Verlag, p. 20
- ↑ Mohr, Hans; Schopfer, Peter (1995), Plant physiology, ISBN 978-3-540-58016-4, Berlin, New York: Springer-Verlag, chapter 19, p. 298
- ↑ Eloi da Silva Pereira. «A importância do logaritmo para a sociedade» (PDF). Encontro Nacional de Educação Matemática. Universidade Estadual da Bahia. Consultado em 3 de dezembro de 2014. Arquivado do original (PDF) em 18 de maio de 2015
- ↑ Eco, Umberto (1989), The open work, ISBN 978-0-674-63976-8, Harvard University Press, seção III.I
- ↑ Sprott, Julien Clinton (2010), Elegant Chaos: Algebraically Simple Chaotic Flows, ISBN 978-981-283-881-0, Nova Jersei: World Scientific, seção 1.9
- ↑ Helmberg, Gilbert (2007), Getting acquainted with fractals, ISBN 978-3-11-019092-2, De Gruyter Textbook, Berlim, Nova Iorque: Walter de Gruyter
- ↑ «Aula 10 — UCG» (PDF). Pontifícia Universidade Católica de Goiás. Janeiro de 2012. Consultado em 3 de dezembro de 2014. Arquivado do original (PDF) em 17 de abril de 2015
- ↑ Ladeira, Luiz Augusto da Costa. «A função logaritmo e a régua de cálculo». Digital Library. Universidade de São Paulo. Consultado em 3 de dezembro de 2014
- ↑ G M. Bruño (1825). Álgebra y trigonometría. [S.l.]: Oxford University Press. p. 24. Consultado em 3 de dezembro de 2014
- ↑ Wright, David (2009), Mathematics and music, ISBN 978-0-8218-4873-9, Providence, RI: AMS Bookstore, capítulo 5
- ↑ Bateman, P. T.; Diamond, Harold G. (2004), Analytic number theory: an introductory course, ISBN 978-981-256-080-3, Nova Jersei: World Scientific, OCLC 492669517, theorem 4.1
- ↑ P. T. Bateman & Diamond 2004, Theorem 8.15
- ↑ Slomson, Alan B. (1991), An introduction to combinatorics, ISBN 978-0-412-35370-3, Londres: CRC Press, capítulo 4
- ↑ Simpson, Thomas (1765). Trigonometry, Plane and Spherical. [S.l.]: Biblioteca Britânica. p. 47
- ↑ Dennis G. Zill (2011). A First Course in Complex Analysis with Applications. [S.l.]: Jones & Bartlett Publishers. p. 95. 405 páginas. ISBN 9781449657529
- ↑ Ganguly, S. (2005), Elements of Complex Analysis, ISBN 978-81-87504-86-3, Kolkata: Academic Publishers, Definition 1.6.3
- ↑ Nevanlinna, Rolf Herman; Paatero, Veikko (2007), Introduction to complex analysis, ISBN 978-0-8218-4399-4, Providence, RI: AMS Bookstore, seção 5.9
- ↑ «Confira este exemplo e faça outros com O Monitor». omonitor.io. Consultado em 25 de março de 2016
- ↑ Moore, Theral Orvis; Hadlock, Edwin H. (1991), Complex analysis, ISBN 978-981-02-0246-0, Singapore: World Scientific, seção 1.2
- ↑ A. S. Fokas (2003). Complex Variables. [S.l.]: 9780521534291. p. 49. 647 páginas. ISBN 9780521534291
- ↑ Wilde, Ivan Francis (2006), Lecture notes on complex analysis, ISBN 978-1-86094-642-4, Londres: Imperial College Press, theorem 6.1.
- ↑ Higham, Nicholas (2008), Functions of Matrices. Theory and Computation, ISBN 978-0-89871-646-7, Philadelphia, PA: SIAM, capítulo 11.
- ↑ Neukirch, Jürgen (1999), Algebraic Number Theory, ISBN 978-3-540-65399-8, Grundlehren der mathematischen Wissenschaften, 322, Berlim: Springer-Verlag, Zbl 0956.11021, MR1697859, seção II.5.
- ↑ Hancock, Edwin R.; Martin, Ralph R.; Sabin, Malcolm A. (2009), Mathematics of Surfaces XIII: 13th IMA International Conference York, UK, September 7–9, 2009 Proceedings, ISBN 978-3-642-03595-1, Springer, p. 379
- ↑ Stinson, Douglas Robert (2006), Cryptography: Theory and Practice, ISBN 978-1-58488-508-5 3ª ed. , Londres: CRC Press
- ↑ Lidl, Rudolf; Niederreiter, Harald (1997), Finite fields, ISBN 978-0-521-39231-0, Cambridge University Press
- ↑ Corless, R.; Gonnet, G.; Hare, D.; Jeffrey, D.; Knuth, Donald (1996), «On the Lambert W function» (PDF), Berlim, Nova Iorque: Springer-Verlag, Advances in Computational Mathematics, ISSN 1019-7168, 5: 329–359, doi:10.1007/BF02124750, consultado em 2 de dezembro de 2014, cópia arquivada (PDF) em 14 de dezembro de 2010
- ↑ Cherkassky, Vladimir; Cherkassky, Vladimir S.; Mulier, Filip (2007), Learning from data: concepts, theory, and methods, ISBN 978-0-471-68182-3, Wiley series on adaptive and learning systems for signal processing, communications, and control, Nova Iorque: John Wiley & Sons, p. 357
- ↑ Bourbaki, Nicolas (1998), General topology. Chapters 5—10, ISBN 978-3-540-64563-4, Elements of Mathematics, Berlim, Nova Iorque: Springer-Verlag, MR 1726872, seção V.4.1
- ↑ Ambartzumian, R. V. (1990), Factorization calculus and geometric probability, ISBN 978-0-521-34535-4, Cambridge University Press, seção 1.4
- ↑ Esnault, Hélène; Viehweg, Eckart (1992), Lectures on vanishing theorems, ISBN 978-3-7643-2822-1, DMV Seminar, 20, Basel, Boston: Birkhäuser Verlag, MR 1193913, seção 2
- ↑ Apostol, T.M. (2010), «Logaritmo», in: Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W., NIST Handbook of Mathematical Functions, ISBN 978-0521192255, Cambridge University Press, MR2723248
Ligações externas[editar | editar código-fonte]
- Hazewinkel, Michiel, ed. (2001), «Logarithmic function», Enciclopédia de Matemática, ISBN 978-1-55608-010-4 (em inglês), Springer
- Colin Byfleet, Educational video on logarithms, consultado em 12 de outubro de 2010
- Edward Wright, Translation of Napier's work on logarithms, consultado em 3 de dezembro de 2014, arquivado do original em 27 de junho de 2007

























![{\displaystyle \log _{b}{\sqrt[{p}]{x}}={\frac {\log _{b}(x)}{p}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2499a9e2a1b1e9e77ccb8dda608b297e0b943f19)





![{\displaystyle \cos \,\alpha \,\cos \,\beta ={\frac {1}{2}}[\cos(\alpha +\beta )+\cos(\alpha -\beta )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55be02a407ad9d4127584bd6d02f3fde6ac05fb9)









![{\displaystyle {\sqrt[{d}]{c}}=c^{\frac {1}{d}}=b^{{\frac {1}{d}}\log _{b}(c)}.\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ba9e10fbda0f1ce9dd2d211ec6bc2c80d1f3dd8)





























![{\displaystyle {\frac {466}{440}}\approx {\frac {493}{466}}\approx 1.059\approx {\sqrt[{12}]{2}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55acf246da64ba711e1717eb43ad81792220ab32)



![{\displaystyle {\begin{aligned}2^{\frac {4}{12}}&={\sqrt[{3}]{2}}\\&\approx 1,2599\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5357209615a2e5b07579fb2fbdcc7d546767e240)


![{\displaystyle \log _{\sqrt[{12}]{2}}(r)=12\log _{2}(r)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/173477b6bc89e2396abacc83ca5015ac01b0747b)






![{\displaystyle \log _{\sqrt[{1200}]{2}}(r)=1200\log _{2}(r)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1ccc3b05bf5ae0d41f85c50ab1a7ceec4e95713)














