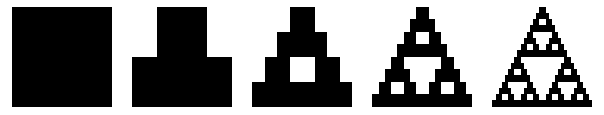Triângulo de Sierpinski

O Triângulo de Sierpinski - também chamado de Junta de Sierpinski - é uma figura geométrica obtida através de um processo recursivo. Ele é uma das formas elementares da geometria fractal por apresentar algumas propriedades, tais como: ter tantos pontos como o do conjunto dos números reais; ter área igual a zero; ser auto-semelhante (uma sua parte é idêntica ao todo); não perder a sua definição inicial à medida que é ampliado. Foi primeiramente descrito em 1915 por Waclaw Sierpinski (1882 - 1969), matemático polonês.
Trata-se de um conjunto autossimilar de um triângulo (na maioria das vezes equilátero). Se dividido em quatro outros triângulos congruentes entre si e entre o triângulo original, cujos vértices são os pontos médios do triângulo de origem, então os subconjuntos do fractal são três cópias escalonadas de triângulos derivados da iterada anterior. O triângulo do meio não pertence ao fractal. Esta separação do fractal em cópias escalonadas pode ser continuada recursivamente nos outros triângulos produzidos. A dimensão fractal do Triângulo de Sierpinski tem os seguintes valores:
Construção[editar | editar código-fonte]
Uma das maneiras de se obter um triângulo de Sierpinski é através do seguinte algoritmo:
- Comece com qualquer triângulo em um plano. O triângulo de Sierpinski canônico utilizava um triângulo equilátero com a base paralela ao eixo horizontal, mas qualquer triângulo pode ser usado (ver primeira figura).
- Encolha o triângulo pela metade (cada lado deve ter metade do tamanho original), faça três copias, e posicione cada triângulo de maneira que encoste nos outros dois em um canto (ver segunda figura).
- Repita o passo 2 para cada figura obtida, indefinidamente (ver a partir da terceira figura).
Embora no processo acima a figura inicial seja um triângulo, não é necessário partir de um para se chegar no triângulo de Sierpinski. É possível utilizar qualquer figura geométrica (ver abaixo), o triângulo só é utilizado por facilitar a visualização.
O fractal propriamente dito só é obtido quando o processo do algoritmo é repetido infinitas vezes, mas conforme o número de iterações aumenta, a imagem obtida tende a se tornar cada vez mais parecida com o fractal.
Este algoritmo ilustra a relação. Em cada etapa, a partir três dos triângulos gerados (semelhantes ao inicial), são criados triângulos com a metade do comprimento lateral e um quarto da superfície que será colorida. O quarto triângulo interno formado a partir disso pode ser visto como um corte da área triangular anterior.
O Triângulo de Sierpinski original, no sentido do rigor matemático, é o objeto limite que permanece mesmo após infinitas iterações. Ele é formado por infinitos vértices. Para ser visualizado, a maioria é realizada através de programas de computador, e, de acordo com a necessidade – se mostrado em tela ou impresso – requer uma recursividade, ou grau de iteração, de no máximo dez. Condicionado pela resolução do meio no qual é exibido (monitor, impressora etc.) e pelo olho humano, estas estruturas não podem mais ser distinguidas do objeto de fronteira. Na clássica mensuração de superfície planimétrica, a área da iteração tende a zero.
Sistema de Lindenmayer[editar | editar código-fonte]
O triângulo de Sierpinski pode ser descrito através das seguintes propriedades do Sistema de Lindenmayer:
- Ângulo: 120°
- Inicializador:
- Regras de derivação:
Propriedades[editar | editar código-fonte]

O triângulo de Sierpinski possui uma dimensão de Hausdorff de (aproximadamente 1,585). Isso acontece porque essa é uma figura formada por três cópias de si mesma, cada uma reduzida por um fator de 1/2.
Também existe uma relação com o triângulo de Pascal. Montando o triângulo de Pascal com 2n linhas, e pintando os números pares de branco e os ímpares de preto, a figura obtida será uma aproximação do triângulo de Sierpinski.
A área de um triângulo de Sierpinski é zero. Isso pode ser percebido quando observamos que, a cada iteração, a área da figura obtida foi reduzida em 25% em relação a área da figura original.
Contextos Matemáticos[editar | editar código-fonte]
Como um fractal clássico, o triângulo de Sierpinski é um paradigma para autossimilaridade exata: os triângulos exteriores formados em cada passo contêm cópias diminutas e exatas do conjunto do fractal. Um escalonamento correspondente de qualquer parte triangular do fractal se parece com a totalidade do objeto. Desta forma, há invariância de escala.
Com base nas leis matemáticas fundamentais, o triângulo de Sierpinski é muito próximo do Conjunto de Cantor. Ambas as dimensões possuem o mesmo inverso multiplicativo de . Isso acontece porque, a cada passo são criados exatos triângulos com um comprimento lateral de . O fractal existe como um objeto limite quando k tende ao infinito, mais precisamente, quando a média de todos os passos da construção é feita e, a partir daí, o “análogo geométrico” pode ser resumido em um limite de uma sequência. A partir da regra de formação também se pode calcular quais pontos da área original pertencem ao objeto limite.
Para calcular a quantidade de triângulos após iterações, pode-se utilizar a seguinte fórmula:
para
Representação por meio do Operador de Hutchinson[editar | editar código-fonte]
Um triângulo de Sierpinski também pode ser representado como atractor de um processo de retroalimentação dinâmica de um processo determinístico de um sistema de funções iterativas, com parâmetros adequados para praticamente todas as figuras geométricas. Desta forma, transformações múltiplas do objeto original são retomadas, estas imagens ordenadas de acordo com a regra do Operador de Hutchinson. Este processo pode ser novamente usado na totalidade do objeto e assim por diante. Caso os parâmetros escolhidos forem os ideais, com o acréscimo de camadas de iteração, as imagens formadas tendem a se tornar um Triangulo de Sierpinski que, neste caso, é o atractor do sistema de funções[1].
Neste sentido, o Triângulo de Sierpinski é caracterizado pelo subconjunto compacto da área que é idêntico à união de suas três imagens sob as transformações homotéticas que dividem o triângulo total em suas respectivas três metades de igual tamanho.
Pirâmide de Sierpinski[editar | editar código-fonte]

Uma representação do Triângulo de Sierpinski – análoga à Esponja de Menger – também é possível na terceira dimensão. Sua figura inicial é um tetraedro. A partir deste centro, um octaedro com metade do comprimento da aresta é recortado em cada iteração. Restarão quatro tetraedros dos quais será recortado, novamente, um octaedro e assim sucessivamente[2]. A dimensão para esta figura é , mesmo que aqui trate-se de uma imagem em espaço tridimensional. Com um número crescente de iterações, o volume da figura tende a zero, no entanto, a superfície permanece constante.
Jogo do Caos[editar | editar código-fonte]

Do ponto de vista da representação recursiva, existe outro algoritmo de ponto aleatório para construção aproximada do Triângulo de Sierpinski: o Jogo do Caos.
Usando esta forma, desenha-se um triângulo equilátero com os vértices A, B, C e se escolhe um ponto aleatório dentro do triângulo (ele também pode estar fora do triângulo sem alterar o resultado substancialmente). Agora, para cada passo deve-se escolher um vértice aleatório (as probabilidades para os cantos são iguais) e o ponto mental precisa ser conectado com o triângulo desenhado. A metade desta seção marca o ponto para a próxima iteração. Se repetido muitas vezes, os pontos criam uma aproximação ao Triângulo de Sierpinski. Se os pontos forem coloridos de acordo com os vértices escolhidos, por exemplo A = verde, B = vermelho e C = azul, obtém-se três Triângulos de Sierpinski coloridos dentro de um Triângulo de Sierpinski.
Pode-se comprovar a partir da estrutura iterativa do Triângulo de Sierpinski que um ponto obtido através deste algoritmo pertence exatamente ao triângulo quando ele também for parte de partida do Triângulo de Sierpinski. Se, por exemplo, escolhe-se um ponto da aresta AB, então se construiu, após infinitas iterações, um Triângulo de Sierpinksi.
Relação com o Triângulo de Pascal[editar | editar código-fonte]
O Triângulo de Pascal é parente do Triângulo de Sierpinski. Os números pares no Triângulo de Pascal correspondem às lacunas no Triângulo de Sierpinksi. Ambos os triângulos possuem uma iteração simples a partir da qual sempre se mostra uma semelhança geométrica: se o Triângulo de Sierpinksi for criado a partir do triângulo inicial descrito acima, então o número de linhas em um Triângulo de Pascal será simplesmente duplicado (números ímpares com mais de uma casa decimal serão representados a seguir como #).
Iniciador:
1
1 1
1º Passo
1
1 1
1 1
1 3 3 1
2º Passo
1
1 1
1 1
1 3 3 1
1 1
1 5 5 1
1 # # 1
1 7 # # # # 7 1
3. ...
Esta semelhança serve tanto para um Triângulo de Pascal infinito quanto para um Triângulo de Sierpinksi após infinitas iterações.
A criação desta semelhança também pode ser interpretada por outro ponto de vista: o próprio triângulo de Pascal é como conceito e, portanto, como modelo geométrico sempre infinito, simplesmente não se pode escrevê-lo por completo. Um Triângulo de Sierpinski produzido iterativamente é, porém, sempre limitado por seu escudo exterior. Desta forma, o Triângulo de Pascal não se aproxima do Triângulo de Sierpinksi por meio de iteração contínua, mas sim o Triângulo de Sierpinski se assemelha ao Triângulo de Pascal por meio do projeto geométrico infinito.

Natureza[editar | editar código-fonte]
Na natureza, este padrão é encontrado na concha do caracol en:Cymbiola innexa[3][4].
Ver também[editar | editar código-fonte]
- ↑ Dr. Jorge Picado. «Atractores de Sierpinski». Consultado em 3 de dezembro de 2014
- ↑ «Die Sierpinski Pyramide»
- ↑ «Max-Planck-Institut für Entwicklungsbiologie». Spiegel online. 12 de Outubro de 2009. Consultado em 12 de Outubro de 2009
- ↑ Bjørn Jamtveit, Paul Meakin (Orgs.). «Growth, Dissolution and Pattern Formation in Geosystems». Kluwer Academic Publishers, Dordrecht 1999