Triângulo de Pascal
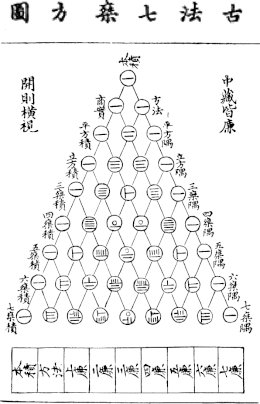
O triângulo de Pascal (alguns países, nomeadamente na Itália, é conhecido como Triângulo de Tartaglia) é um triângulo numérico infinito formado por números binomiais , onde representa o número da linha e representa o número da coluna, iniciando a contagem a partir do zero.[1] Na China aparece nas obras de Chu Shi-kié no século XII, na Pérsia o poeta e matemático Omar Khayyám do século XII o utiliza para descobrir raízes n-ésimas, na Alemanha o triângulo aparece no livro de Petrus Apianus no século XVI. No entanto, foi Blaise Pascal que estudou e utilizou as propriedades do triângulo na teoria das probabilidades. O triângulo também pode ser representado como:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | |
| 2 | 1 | 3 | 6 | 10 | 15 | ||
| 3 | 1 | 4 | 10 | 20 | |||
| 4 | 1 | 5 | 15 | ||||
| 5 | 1 | 6 | |||||
| 6 | 1 |
Ele define os números no triângulo por recursão: Chame o número na (m+1)-ésima linha e na (n+1)-ésima coluna por tmn. Então tmn = tm-1,n-1 + tm-1,n, para m = 0, 1, 2... e n = 0, 1, 2... As condições de contorno são tm, −1 = 0, t−1, n para m = 1, 2, 3... e n = 1, 2, 3... O gerador t00 = 1. Pascal conclui com a prova,
Propriedades[editar | editar código-fonte]
Relação de Stifel[editar | editar código-fonte]

Cada número do triângulo de Pascal é igual à soma do número imediatamente acima e do antecessor do número de cima.
Portanto:
Soma de uma linha[editar | editar código-fonte]
A soma de uma linha no triângulo de Pascal é igual a .
Soma de uma coluna[editar | editar código-fonte]
A soma da coluna, no triângulo de Pascal, pode ser calculada pela relação .
Portanto:
Simetria[editar | editar código-fonte]
O triângulo de Pascal apresenta simetria em relação à altura, se for escrito da seguinte forma:
Isso deve-se ao fato de que
Soma de uma diagonal[editar | editar código-fonte]
Conhecendo as fórmulas (Soma de uma coluna) e (Simetria) do triângulo de Pascal, pode-se encontrar a seguinte fórmula para soma de diagonais: .
Novas propriedades – Desigualdades[editar | editar código-fonte]
Em 2014 foram descobertas novas propriedades, envolvendo Desigualdades, quais sejam:[3]
1- Em toda a infinita coluna central do Triângulo, na figura abaixo, o produto de dois de seus elementos é maior do que o produto de dois elementos pertencentes à mesma coluna central, localizados simetricamente entre eles. Por exemplo, na figura abaixo: 1 x 20 > 2 x 6, ou então, 2 x 20 > 6 x 6, ou ainda, 1 x 6 > 2 x 2. Isto vale para toda a coluna central.
2- Dados dois elementos A e B da coluna central, o produto deles é maior do que o produto de dois elementos C e D pertencentes às diagonais que passam por A e por B, que estejam simetricamente localizados em relação a A e a B. Por exemplo, olhando novamente a figura acima: se A = 2 e B = 20, então:
2 x 20 > 3 x 10 > 4 x 4 > 1 x 5.
Se A = 1 e B = 20, então:
1 x 20 > 1 x 10 > 1 x 4 > 1 x 1.
Algoritmos[editar | editar código-fonte]
Python[editar | editar código-fonte]
Recursivo[editar | editar código-fonte]
def pascal_t(m,n):
if m == 0 and n ==0:
return 1
elif n == -1 or m == -1:
return 0
else:
return pascal_t(m-1, n-1) + pascal_t(m-1,n)
Programado[editar | editar código-fonte]
def pascal_tri(lines):
t= [[0 for i in range(lines)] for i in range(lines)]
for n in range(lines):
for k in range(lines):
if n == 0 and k == 0:
t[n][k] = 1
elif n > -1 and k > -1:
t[n][k] = t[n-1][k-1] + t[n-1][k]
return t
Java[editar | editar código-fonte]
public void Pascal(int n) {
int nfilas = n;
int[] a = new int[1];
for (int i = 1; i <= nfilas; i++) {
int[] x = new int[i];
for (int j = 0; j < i; j++) {
if (j == 0 || j == (i - 1)) {
x[j] = 1;
} else {
x[j] = a[j] + a[j - 1];
}
System.out.print(x[j] + " ");
}
a = x;
System.out.println();
}
}
Notas[editar | editar código-fonte]
- ↑ Kadane (2011), p. 62.
- ↑ «Confira este exemplo e faça outros com O Monitor». omonitor.io. Consultado em 18 de março de 2016
- ↑ Antônio Luiz de Melo, Rogério César dos Santos (13 de março de 2014). «Desigualdades no Triângulo de Pascal» (PDF). Revista Eletrônica Paulista de Matemática. Consultado em 6 de abril de 2015[fonte confiável?]
Referências[editar | editar código-fonte]
- Kadane, J.B. (2011). Principles of Uncertainty (em inglês). Boca Raton: CRC Press. ISBN 9781439861615
Ver também[editar | editar código-fonte]
















