Temperamento igual

ⓘ
Um temperamento igual é um sistema de afinação ou temperamento musical que aproxima intervalos justos dividindo uma oitava (ou outro intervalo) em etapas iguais. Isso significa que a razão entre as frequências de qualquer par de notas adjacentes é a mesma, o que resulta em um tamanho de etapa percebido como igual, já que a altura é percebida aproximadamente como o logaritmo da frequência.[2]
Na música clássica e na música ocidental em geral, o sistema de afinação mais comum desde o século XVIII tem sido o temperamento igual de 12 tons (também conhecido como temperamento igual de 12 notas, 12-TET ou 12-ET), que divide a oitava em 12 partes, todas iguais em uma escala logarítmica, com uma razão igual à raiz 12ª de 2 (12√2 ≈ 1.05946). O menor intervalo resultante, 1⁄12 da largura de uma oitava, é chamado de semitom ou meio tom. Nos países ocidentais, o termo temperamento igual, sem qualificação, geralmente se refere ao 12-TET.
Nos tempos modernos, o 12-TET é geralmente afinado em relação a um tom-padrão de 440 Hz, chamado de Lá 440, o que significa que uma nota, Lá, é afinada em 440 hertz e todas as outras notas são definidas como múltiplos de semitons acima ou abaixo dela, em frequência. O tom-padrão nem sempre foi de 440 Hz; ele variou consideravelmente e, em geral, aumentou nos últimos poucos séculos.[3]
Outros temperamentos iguais dividem a oitava de maneira diferente. Por exemplo, algumas músicas foram escritas em 19-TET e 31-TET, enquanto o sistema de tons árabe usa 24-TET.
Em vez de dividir uma oitava, um temperamento igual também pode dividir um intervalo diferente, como a versão temperada igualmente da escala Bohlen-Pierce, que divide o intervalo justo de uma oitava e quinta (razão 3:1), chamado de "tritave" ou "pseudo-oitava" nesse sistema, em 13 partes iguais.
Para sistemas de afinação que dividem a oitava igualmente, mas não são aproximações de intervalos justos, o termo divisão igual da oitava, ou EDO em inglês, pode ser usado.
Ensembles de cordas sem trastes, que podem ajustar a afinação de todas as notas, exceto as cordas soltas, e grupos vocais, que não têm limitações mecânicas de afinação, às vezes usam uma afinação muito mais próxima da justa entonação por razões acústicas. Outros instrumentos, como alguns instrumentos de sopro, teclado e com trastes, muitas vezes apenas aproximam o temperamento igual, onde limitações técnicas impedem afinações exatas.[4] Alguns instrumentos de sopro que podem curvar facilmente seu tom, mais notavelmente trombones, usam afinação semelhante a ensembles de cordas e grupos vocais.
Propriedades gerais[editar | editar código-fonte]
Em um temperamento igual, a distância entre dois passos adjacentes da escala é o mesmo intervalo. Como a identidade percebida de um intervalo depende da sua razão, essa escala em passos iguais é uma sequência geométrica de multiplicações. (Uma sequência aritmética de intervalos não soaria espaçada uniformemente e não permitiria transposição para diferentes tonalidades.) Especificamente, o menor intervalo em uma escala temperada igual é a razão:
Onde a razão r divide a razão p (tipicamente a oitava, que é 2:1) em n partes iguais.
As escalas são frequentemente medidas em cents, que dividem a oitava em 1200 intervalos iguais (cada um chamado de cent). Essa escala logarítmica torna mais fácil a comparação de diferentes sistemas de afinação do que a comparação de razões e tem um uso considerável na etnomusicologia. O passo básico em cents para qualquer temperamento igual pode ser encontrado tomando a largura de p acima em cents (geralmente a oitava, que tem 1200 cents de largura), chamada de w abaixo, e dividindo-a em n partes:
Na análise musical, o material pertencente a um temperamento igual muitas vezes é representado por uma notação inteira, o que significa que um único número inteiro é usado para representar cada altura. Isso simplifica e generaliza a discussão do material de altura dentro do temperamento de modo similar ao que tomar o logaritmo de uma multiplicação a reduz a uma adição. Além disso, aplicando a aritmética modular onde o módulo é o número de divisões da oitava (geralmente 12), esses números inteiros podem ser reduzidos a classes de tons, o que remove a distinção (ou reconhece a similaridade) entre alturas com o mesmo nome, por exemplo, dó é 0 independentemente do registro da oitava. O padrão de codificação MIDI usa designações de nota inteiras.
Temperamento igual de doze tons[editar | editar código-fonte]
O temperamento igual de doze tons, que divide a oitava em 12 intervalos de tamanho igual, é o sistema musical mais amplamente utilizado hoje, especialmente na música ocidental." Essa frase explica o que é o "12-tone equal temperament" e destaca sua importância no contexto da música ocidental.
História[editar | editar código-fonte]
As duas figuras frequentemente creditadas com a conquista do cálculo exato do temperamento igual são Zhu Zaiyu (também romanizado como Chu-Tsaiyu. Chinês: 朱載堉) em 1584 e Simon Stevin em 1585. De acordo com Fritz A. Kuttner, um crítico da teoria,[5] sabe-se que Zhu "apresentou um método altamente preciso, simples e engenhoso para o cálculo aritmético de monocórdios de temperamento igual em 1584" e que Stevin "ofereceu uma definição matemática de temperamento igual, além de um cálculo um pouco menos preciso dos valores numéricos correspondentes em 1585 ou posteriormente". Os desenvolvimentos ocorreram de forma independente.[6]
Kenneth Robinson atribui a invenção do temperamento igual a Zhu[7] e fornece citações textuais como evidência.[8] Em um texto datado de 1584, Zhu escreveu: "Eu fundei um novo sistema. Eu estabeleço um pé como o número do qual os outros devem ser extraídos e, usando proporções, eu os extraio. No total, tem-se que encontrar as figuras exatas para os tocadores de pitch em doze operações."[8] Kuttner discorda e observa que sua afirmação "não pode ser considerada correta sem grandes qualificações".[5] Kuttner propõe que nem Zhu nem Stevin alcançaram o temperamento igual e que nenhum dos dois deve ser considerado um inventor.[9]
China[editar | editar código-fonte]

A China havia anteriormente desenvolvido aproximações para o temperamento igual de 12 notas, mas Zhu foi a primeira pessoa a resolver matematicamente o temperamento igual de 12 notas,[10] o qual ele descreveu em sua obra Fusão da Música e do Calendário (律暦融通) em 1580 e Compendium Completo de Música e Afinação (Yuelü quan shu 樂律全書) em 1584.[11] Joseph Needham também fornece uma conta detalhada.[12] Zhu obteve seu resultado dividindo o comprimento da corda e do tubo sucessivamente por 12√2 ≈ 1.059463 e para o comprimento do tubo por 24√2,[13] de modo que após 12 divisões (uma oitava), o comprimento era reduzido pela metade.
Zhu criou vários instrumentos ajustados ao seu sistema, incluindo tubos de bambu.[14]
Europa[editar | editar código-fonte]
Alguns dos primeiros europeus a defenderem o temperamento igual foram os alaudistas Vincenzo Galilei, Giacomo Gorzanis e Francesco Spinacino, todos eles compositores que escreveram música utilizando este sistema.[15][16][17][18]
Simon Stevin foi o primeiro a desenvolver o 12-TET com base na raiz duodécima de dois, o qual ele descreveu em Van De Spiegheling der singconst (cerca de 1605), publicado postumamente em 1884.[19]
Os músicos que tocavam instrumentos de cordas dedilhadas, como alaúd e violão, geralmente preferiam o temperamento igual,[20] enquanto outros eram mais divididos.[21] No final, o temperamento igual de 12 tons prevaleceu. Isso permitiu a modulação enarmônica, novos estilos de tonalidade simétrica e politonalidade, música atonal como a escrita com a técnica dos 12 tons ou serialismo, e o jazz (pelo menos sua componente de piano) se desenvolver e florescer.
Matemática[editar | editar código-fonte]

No temperamento igual de 12 tons, que divide a oitava em 12 partes iguais, a largura de um semitom, isto é, a razão de frequência do intervalo entre duas notas adjacentes, é a raiz duodécima de dois:
Este intervalo é dividido em 100 cents.
Calculando frequências absolutas[editar | editar código-fonte]
Para encontrar a frequência, Pn, de uma nota em 12-TET, pode ser usada a seguinte definição:
Nesta fórmula, Pn é a altura, ou frequência (geralmente em hertz), que você está tentando encontrar. Pa é a frequência de uma altura de referência. n e a são números atribuídos à altura desejada e à altura de referência, respectivamente. Esses dois números vêm de uma lista de inteiros consecutivos atribuídos a semitons consecutivos. Por exemplo, A4 (a altura de referência) é a 49ª tecla da extremidade esquerda de um piano (afinado em 440 Hz), e C4 (Dó central) e F#4 são a 40ª e 46ª teclas, respectivamente. Esses números podem ser usados para encontrar a frequência de C4 e F#4:
Convertendo frequências para seus equivalentes em temperamento igual[editar | editar código-fonte]
Para converter uma frequência (em Hz) para sua contraparte igual em 12-TET, a seguinte fórmula pode ser usada:
En é a frequência de um pitch em temperamento igual, e a é a frequência de um pitch de referência. Por exemplo, se considerarmos o pitch de referência igual a 440 Hz, podemos ver que as frequências de E5 e C#5 são, respectivamente:
Comparação com a afinação justa[editar | editar código-fonte]
Os intervalos de 12-TET se aproximam de forma próxima de alguns intervalos de afinação justa.[22] Os quintos e quartos são quase indistinguivelmente próximos de intervalos justos, enquanto terças e sextas estão mais distantes.
Na tabela a seguir, os tamanhos de vários intervalos justos são comparados com seus equivalentes temperados em 12 notas, dados como uma proporção bem como em centésimos.
| Nome do Intervalo | Valor exato em 12-TET | Valor decimal em 12-TET | Cents | Intervalo na afinação justa | Cents na afinação justa | Diferença |
|---|---|---|---|---|---|---|
| Uníssono (C) | 20⁄12 = 1 | 1 | 0 | 1⁄1 = 1 | 0 | 0 |
| Segunda menor (D♭) | 21⁄12 = 12√2 | 1.059463 | 100 | 16⁄15 = 1.06666… | 111.73 | -11.73 |
| Segunda maior (D) | 22⁄12 = 6√2 | 1.122462 | 200 | 9⁄8 = 1.125 | 203.91 | -3.91 |
| Terça menor (E♭) | 23⁄12 = 4√2 | 1.189207 | 300 | 6⁄5 = 1.2 | 315.64 | -15.64 |
| Terça maior (E) | 24⁄12 = 3√2 | 1.259921 | 400 | 5⁄4 = 1.25 | 386.31 | +13.69 |
| Quarta justa (F) | 25⁄12 = 12√32 | 1.33484 | 500 | 4⁄3 = 1.33333… | 498.04 | +1.96 |
| Trítono (G♭) | 26⁄12 = √2 | 1.414214 | 600 | 64⁄45= 1.42222… | 609.78 | -9.78 |
| Quinta justa (G) | 27⁄12 = 12√128 | 1.498307 | 700 | 3⁄2 = 1.5 | 701.96 | -1.96 |
| Sexta menor (A♭) | 28⁄12 = 3√4 | 1.587401 | 800 | 8⁄5 = 1.6 | 813.69 | -13.69 |
| Sexta maior (A) | 29⁄12 = 4√8 | 1.681793 | 900 | 5⁄3 = 1.66666… | 884.36 | +15.64 |
| Sétima menor (B♭) | 210⁄12 = 6√32 | 1.781797 | 1000 | 16⁄9 = 1.77777… | 996.09 | +3.91 |
| Sétima maior (B) | 211⁄12 = 12√2048 | 1.887749 | 1100 | 15⁄8= 1.875 | 1088.270 | +11.73 |
| Oitava (C) | 212⁄12 = 2 | 2 | 1200 | 2⁄1 = 2 | 1200.00 | 0 |
Sete divisões iguais da quinta[editar | editar código-fonte]
Violinos, violas e cellos são afinados em quintas perfeitas (G–D–A–E para violinos e C–G–D–A para violas e cellos), o que sugere que sua razão de semitom é ligeiramente mais alta do que na convencional equalização de 12 tons. Como uma quinta perfeita está na relação de 3:2 com o seu tom base, e esse intervalo compreende sete etapas, cada tom está na razão de 7√3⁄2 para o próximo (100,28 cents), o que proporciona uma quinta perfeita com uma razão de 3:2, mas com uma oitava ligeiramente ampliada com uma razão de ≈ 517:258 ou ≈ 2.00388:1, em vez do usual 2:1, porque 12 quintas perfeitas não correspondem a sete oitavas.[23] Durante a execução, no entanto, o violinista escolhe as notas pelo ouvido, e apenas as quatro notas das cordas soltas garantem essa razão de 3:2.
Referências
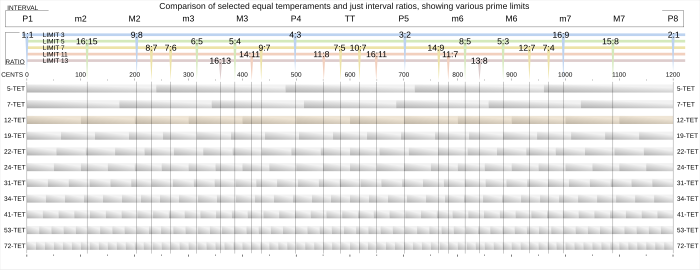
- ↑ Sethares compara vários temperamentos iguais em um gráfico com os eixos invertidos em relação aos eixos na primeira comparação de temperamentos iguais, e com eixos idênticos na segunda.(fig. 4.6, p. 58)
- ↑ O'Donnell, Michael. «Perceptual Foundations of Sound». Consultado em 11 de março de 2017
- ↑ The History of Musical Pitch in Europe p493-511 Herman Helmholtz, Alexander J. Ellis On The Sensations of Tone, Dover Publications, Inc., New York
- ↑ Varieschi, G., & Gower, C. (2010). Intonation and compensation of fretted string instruments. American Journal of Physics, 78(47), 47-55. https://doi.org/10.1119/1.3226563
- ↑ a b Fritz A. Kuttner. p. 163.
- ↑ Fritz A. Kuttner. "Prince Chu Tsai-Yü's Life and Work: A Re-Evaluation of His Contribution to Equal Temperament Theory", p.200, Ethnomusicology, Vol. 19, No. 2 (May 1975), pp. 163–206.
- ↑ Kenneth Robinson: A critical study of Chu Tsai-yü's contribution to the theory of equal temperament in Chinese music. (Sinologica Coloniensia, Bd. 9.) x, 136 pp. Wiesbaden: Franz Steiner Verlag GmbH, 1980. DM 36. p.vii "Chu-Tsaiyu the first formulator of the mathematics of "equal temperament" anywhere in the world
- ↑ a b Robinson, Kenneth G., and Joseph Needham. 1962. "Physics and Physical Technology". In Science and Civilisation in China, vol. 4: "Physics and Physical Technology", Part 1: "Physics", edited by Joseph Needham. Cambridge: University Press. p. 221.
- ↑ Fritz A. Kuttner. p. 200.
- ↑ Gene J. Cho "The Significance of the Discovery of the Musical Equal Temperament in the Cultural History," http://en.cnki.com.cn/Article_en/CJFDTOTAL-XHYY201002002.htm Arquivado em 2012-03-15 no Wayback Machine
- ↑ «Quantifying Ritual: Political Cosmology, Courtly Music, and Precision Mathematics in Seventeenth-Century China Roger Hart Departments of History and Asian Studies, University of Texas, Austin». Uts.cc.utexas.edu. Consultado em 20 de março de 2012. Arquivado do original em 5 de março de 2012
- ↑ Science and Civilisation in China, Vol IV:1 (Physics), Joseph Needham, Cambridge University Press, 1962–2004, pp 220 ff
- ↑ The Shorter Science & Civilisation in China, An abridgement by Colin Ronan of Joseph Needham's original text, p385
- ↑ Lau Hanson, Abacus and Practical Mathematics p389 (em Chinês 劳汉生 《珠算与实用数学》 389页)
- ↑ Galilei, V. (1584). Il Fronimo... Dialogo sopra l'arte del bene intavolare. G. Scotto: Venice, ff. 80–89.
- ↑ «Resound – Corruption of Music». Philresound.co.uk. Consultado em 20 de março de 2012. Arquivado do original em 24 de março de 2012
- ↑ Giacomo Gorzanis, c. 1525 – c. 1575 Intabolatura di liuto. Geneva, 1982
- ↑ «Spinacino 1507a: Thematic Index». Appalachian State University. Consultado em 14 de junho de 2012. Arquivado do original em 25 de julho de 2011
- ↑ «Van de Spiegheling der singconst, ed by Rudolf Rasch, The Diapason Press». Diapason.xentonic.org. 30 de junho de 2009. Consultado em 20 de março de 2012. Arquivado do original em 17 de julho de 2011
- ↑ "Lutes, Viols, Temperaments" Mark Lindley ISBN 978-0-521-28883-5
- ↑ Andreas Werckmeister: Musicalische Paradoxal-Discourse, 1707
- ↑ Partch, Harry (1979). Genesis of a Music 2nd ed. [S.l.]: Da Capo Press. p. 134. ISBN 0-306-80106-X
- ↑ Cordier, Serge. «Le tempérament égal à quintes justes» (em francês). Association pour la Recherche et le Développement de la Musique. Consultado em 2 de junho de 2010



![{\displaystyle r={\sqrt[{n}]{p}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b55fb394d767c50fb569ca27fd636072c72fbd7c)

![{\displaystyle {\sqrt[{12}]{2}}=2^{\frac {1}{12}}\approx 1.059463}](https://wikimedia.org/api/rest_v1/media/math/render/svg/232c2beab28b1c46c328080d982595d9ef196e08)
![{\displaystyle P_{n}=P_{a}\left({\sqrt[{12}]{2}}\right)^{(n-a)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3381e111c79f7e16a073bbe05c6cabeaba2ff79a)
![{\displaystyle P_{40}=440\left({\sqrt[{12}]{2}}\right)^{(40-49)}\approx 261.626\ \mathrm {Hz} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f16dc9af5bbe778786f73eca304c80c72584cd70)
![{\displaystyle P_{46}=440\left({\sqrt[{12}]{2}}\right)^{(46-49)}\approx 369.994\ \mathrm {Hz} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c7144b8e3148077acb97a47d384a62a1f2a5445)


