Teoria espectral de grafos

O grafo completo com 8 vértices possui espectro {7,-1,-1,-1,-1,-1,-1,-1} .

Em matemática, a teoria espectral de grafos estuda propriedades de um grafo por meio de suas representações matriciais e de seus respectivos espectros. Em geral, a Teoria Algébrica dos Grafos estuda propriedades algébricas de funções de representação e operações em grafos, conceitos e propriedades algébricas delas decorrentes. Além disso, em Teoria Espectral de Grafos, estudam-se as propriedades estruturais decorrentes das matrizes que representam grafos. Estas últimas levam às propriedades espectrais das matrizes de representação, que é o elemento central da teoria espectral de grafos.

Breve Histórico

Teoria Espectral de Grafos surgiu nos anos 1950 e 1960. Além das pesquisas em Teoria dos Grafos sobre a relação entre as propriedades estruturais e espectrais de grafos, outra fonte importante foi a pesquisa em química quântica, mas as conexões entre essas duas linhas de trabalho foram descobertos muito mais tarde. A monografia Spectra of graphs de 1980, por Cvetkovic, Doob, e Sachs resumiu quase todas as pesquisas até o momento na área. Em 1988, ela foi atualizada pelo survey em Teoria Espectral de Grafos Recent Results in the Theory of Graph Spectra. A 3 ª edição do Spectra of graphs (1995) contém um resumo das contribuições mais recentes para o assunto.

Matriz de Adjacência

O estudo da Teoria Espectral dos Grafos basicamente relaciona propriedades algébricas do espectro de certas matrizes associadas a um grafo e as propriedades estruturais desse grafo. A associação mais comum é feita pela matriz de adjacência e o espectro dessa matriz é o espectro do grafo. Dado um grafo G=(V,E) com n vértices, a matriz de adjacência de G é a matriz de ordem n dada por $A(G)=[a_{ij}]$, onde $a_{ij}=1$ se $v_{i}v_{j}\in E$ e $a_{ij}=0$ nas entradas restantes. Quando conveniente, utilizaremos apenas A para denotar a matriz de adjacência. Eis um exemplo:

Grafo rotulado	Matriz de Adjacência
	${\begin{bmatrix}1&1&0&0&1&0\\1&0&1&0&1&0\\0&1&0&1&0&0\\0&0&1&0&1&1\\1&1&0&1&0&0\\0&0&0&1&0&0\\\end{bmatrix}}$

O espectro de G é o conjunto dos autovalores, geralmente apresentados em ordem decrescente, não necessariamente no sentido estrito, associados às suas respectivas multiplicidades algébricas.

Grafos Isoespectrais

Uma das questões em aberto da Teoria de Grafos se refere à caracterização de uma lista completa de parâmetros capaz de decidir se dois grafos são isomorfos. Tais parâmetros são conhecidos como invariantes do grafo. Dois grafos são chamados de isoespectrais ou cospectrais se a matriz de adjacência de cada grafo tem os mesmos autovalores.

Grafos isospectrais não precisam ser isomorfos, mas os grafos isomorfos são isoespectrais. O menor par de grafos não isomorfos e cospectrais não dirigidos são {K_1,4, C₄ U K₁}, como relatado por Collatz e Sinogowitz em 1957.

Quase todas as árvores são coespectrais, ou seja, a proporção de árvores cospectrais em n vértices tende a 1 quando n cresce.

Energia do Grafo

Se A é a matriz de adjacência do grafo G, a energia do grafo é definida como:

$E(G)=\sum _{i=1}^{n}|\lambda _{i}|$

onde $\lambda _{i}$, $i=1,2,\ldots ,n$ são os autovalores de A. A energia de um grafo foi definida pela primeira vez por Ivan Gutman em 1978.

Matriz Laplaciana

Dado um grafo G=(V,E) com n vértices, a matriz Laplaciana de G é a matriz de ordem n dada por $L(G)=[l_{ij}]$, onde $l_{ij}=-1$ se $v_{i}v_{j}\in E$, $l_{ii}=d(v_{i})$ e $l_{ij}=0$ nas entradas restantes. Quando conveniente, utilizaremos apenas L para denotar a matriz laplaciana.

A matriz Laplaciana e a matriz de adjacência se relacionam da forma

$L=D-A$

onde $D$ é a matriz diagonal com o grau dos vértices.

Eis um exemplo:

Grafo rotulado	Matriz laplaciana
	${\begin{bmatrix}2&-1&0&0&-1&0\\-1&3&-1&0&-1&0\\0&-1&2&-1&0&0\\0&0&-1&3&-1&-1\\-1&-1&0&-1&3&0\\0&0&0&-1&0&1\\\end{bmatrix}}$

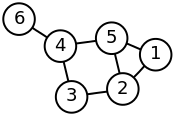
Uma representação de um grafo frequente em teoria espectral de grafos é dada pela sua matriz Laplaciana. Essa matriz e, em especial, o seu segundo menor autovalor, chamado de conectividade algébrica, desempenham um papel relevante em diversas aplicações. Em, alguns dos muitos resultados conhecidos sobre essa matriz são exibidos.

A seguir, enunciamos um resultado bem conhecido sobre o primeiro e o segundo menor autovalor laplaciano de um grafo G.

Teorema

Seja G um grafo com n vértices, e L sua matriz laplaciana. Sejam ${l_{1}}\leq {l_{2}}\leq {...}\leq {l_{n}}$ os autovalores de L. Então:

(i) ${l_{1}}=0$ e o vetor com todas entradas iguais a 1 é autovetor associado

(ii) G é conexo se, e somente se, ${l_{2}}>0$.

Portanto todos os autovalores de L são maiores ou iguais a zero. Para um grafo desconexo, o número de autovalores iguais a zero é precisamente o número de componentes conexas do grafo. Assim, a multiplicidade do autovalor zero é o número de componentes conexas de G.

Teorema da Matriz-Árvore

Outro resultado importante envolvendo a matriz Laplaciana é o teorema da matriz-árvore. Uma árvore geradora de um grafo G é um subgrafo que tem os mesmos vértices de G e é uma árvore. A determinação do número de árvores geradoras de um grafo é um dos problemas mais antigos e famosos da teoria de grafos.

Em 1847, Kirchhoff estudando circuitos elétricos, provou o resultado que ficou conhecido como teorema da matriz-árvore, enunciado a seguir.

Claramente, grafos desconexos não possuem árvores geradoras. Por outro lado, todo grafo conexo tem pelo menos uma árvore geradora (se o grafo não é uma árvore, podemos remover uma aresta de cada ciclo, sucessivamente, até não haver mais ciclos. O subgrafo obtido será uma árvore geradora do grafo inicial). O teorema da matriz-árvore, na sua versão original, afirma que o número de árvores geradoras de um grafo é dado por qualquer cofator de sua matriz laplaciana. Mais precisamente:

Teorema

adj(L) = t(G) · J, onde t(G) é o número de árvores geradoras de G, e J é a matriz com todas entradas iguais a 1.

Conectividade algébrica

O icosaedro truncado, visto como um grafo, possui conectividade de vértices 3, porém conectividade algébrica de 0,243.

Fiedler mostrou que um grafo é conexo se, e somente se, o seu segundo menor autovalor Laplaciano é positivo. Esse autovalor é denominado conectividade algébrica e desempenha um papel fundamental em teoria espectral de grafos. Denotamos a conectividade algébrica por a(G).

As conectividades algébrica, de vértices e de arestas, respectivamente a(G), κ(G) e λ(G), estão relacionadas de acordo com o resultado abaixo, provado por Fiedler.

Teorema

Se G não é um grafo completo então a(G) ≤ κ(G) ≤ λ(G).

Para o grafo completo ${K_{n}}$, Fiedler demonstrou que $a({K_{n}})=n$.

Energia Laplaciana do Grafo

Da mesma maneira que para a matriz de adjacência, a energia pode ser definida utilizando os autovalores da matriz Laplaciana. Esse conceito também foi definido por Ivan Gutman em 2006 no artigo. Considerando L a matriz Laplaciana do grafo G com n vértices e m arestas, a energia Laplaciana do grafo é definida como:

$E(G)=\sum _{i=1}^{n}\left|\lambda _{i}-{\frac {2m}{n}}\right|$

onde $\lambda _{i}$, $i=1,2,\ldots ,n$ são os autovalores de L.

Matriz Laplaciana normalizada

A matriz Laplaciana normalizada pode ser definida por

$\ell _{i,j}:={\begin{cases}1&{\mbox{if}}\ i=j\ {\mbox{and}}\ \deg(v_{i})\neq 0\\-{\frac {1}{\sqrt {\deg(v_{i})\deg(v_{j})}}}&{\mbox{if}}\ i\neq j\ {\mbox{and}}\ v_{i}{\mbox{ is adjacent to }}v_{j}\\0&{\mbox{otherwise}}.\end{cases}}$

A matriz Laplaciana normalizada $\ell$ e a matriz Laplaciana $L$ se relacionam da seguinte forma

$\ell =D^{1/2}LD^{1/2}$

onde $D$ diagonal com o grau dos vértices.

Ver também

• Matriz de adjacência
• Conectividade algébrica
• Energia do grafo