Triângulo de Reuleaux
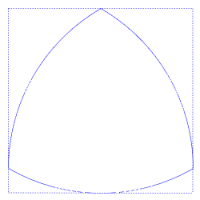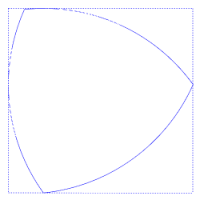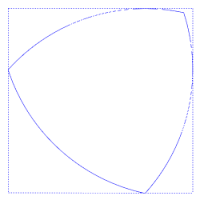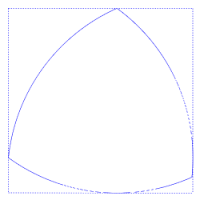
O triângulo de Reuleaux (ou triângulo esférico) é o exemplo mais simples dos chamados polígonos de Reuleaux. O nome é uma homenagem ao cientista e engenheiro que os desenvolveu, Franz Reuleaux. Estes polígonos tem a distinção de serem curvas de largura constante, ou seja, a distância entre os duas retas tangentes paralelas opostas é a mesma, independentemente da direção destas retas. Isto é mostrado na figura anexa, em que há sempre quatro pontos de contato com o quadrado, uma de cada lado.[1]
Construção[editar | editar código-fonte]

Um triângulo de Reuleaux pode ser tanto construído diretamente a partir de três círculos, ou pelo arredondamento dos lados de um triângulo equilátero.[2]
A construção com três círculos pode ser realizada com compasso sozinho, sem a necessidade de uma régua. Pelo teorema de Mohr-Mascheroni, o mesmo vale para qualquer construção com régua e compasso,[3] mas a construção do triângulo de Reuleaux é particularmente simples:
Primeiro, usa-se o compasso para desenhar o círculo, ou um arco circular suficientemente grande. Em seguida, mantendo-se fixa a abertura do compasso, coloca-se a ponta do compasso sobre o círculo ou arco, e desenha-se um segundo círculo ou arco passando pelo centro do primeiro. Finalmente, com a ponta do compasso em um dos dois pontos de interseção dos dois círculos, desenha-se um terceiro círculo ou arco de mesmo raio, através dos centros dos dois primeiros círculos. A região central do arranjo correspondente de três círculos é um triângulo de Reuleaux.[2]
Alternativamente, constrói-se um triângulo equilátero T. Então desenha-se os arcos dos círculos, cada um centrado em um vértice de T e conectando os outros dois vértices.[4]
Outros ficheiros[editar | editar código-fonte]
-
Triângulo de Reuleaux
Referências
- ↑ Clifford A. Pickover; The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics; Sterling Publishing Company, Inc., 2009. pg 266. - books.google.com.br
- ↑ a b Hann, Michael (2014), Structure and Form in Design: Critical Ideas for Creative Practice, ISBN 9781472584311, A&C Black, p. 34.
- ↑ Hungerbühler, Norbert (1994), «A short elementary proof of the Mohr-Mascheroni theorem», The American Mathematical Monthly, 101 (8): 784–787, MR 1299166, doi:10.2307/2974536.
- ↑ Gardner, Martin (2014), «Chapter 18: Curves of Constant Width», Knots and Borromean Rings, Rep-Tiles, and Eight Queens, ISBN 9780521756136, The New Martin Gardner Mathematical Library, 4, Cambridge University Press, pp. 223–245.

