Polígono

Em geometria, um polígono é uma figura fechada com lados. A palavra "polígono" vem da palavra em grego "polígonos" que significa ter muitos lados ou ângulos.[1] A definição usada por Euclides para polígono era uma figura limitada por linhas retas, sendo que essas linhas deveriam ser mais de quatro, e figura qualquer região do plano cercada por uma ou mais bordas.[2]
Definição[editar | editar código-fonte]

Linha poligonal[editar | editar código-fonte]

Linha poligonal é uma sucessão de segmentos consecutivos e não-colineares, dois a dois. Denotamos uma linha poligonal fornecendo a sequência dos pontos extremos dos segmentos que a formam. Ou seja, a linha poligonal corresponde a reunião dos segmentos ..., [3][4]
Classificação[editar | editar código-fonte]
Uma linha poligonal é classificada em:
- aberta - quando os extremos e não coincidem;
- fechada - quando os extremos e coincidem;
- simples - quando a interseção de qualquer dois segmentos não consecutivos é vazia;
- não-simples - quando não é simples.
Polígono[editar | editar código-fonte]

Polígono é a região plana limitada por uma linha poligonal fechada. Denotamos um polígono de forma similar a que denotamos uma linha poligonal. Isto é, um polígono corresponde à região limitada pela reunião dos segmentos ..., e [5]
Na literatura, também encontramos o termo polígono como sinônimo de linha poligonal fechada. Neste caso, a região plana limitada pelo polígono é chamada de seu interior e a união do polígono com seu interior é chamada de região poligonal ou superfície poligonal.[5]
Elementos[editar | editar código-fonte]
Um polígono possui os seguintes elementos:[5]
- vértice - extremo de um dos segmentos que formam o polígono, i.e. são vértices os pontos ...,
- lado - segmento que forma o polígono, i.e. são lados os segmentos ..., e
- diagonais - segmentos de reta com extremidades em vértices não consecutivos;
- ângulo (interno) - ângulo formado por dois lados consecutivos, i.e. os ângulos ...,
- ângulo externo - ângulo suplementar e adjacente a um ângulo interno.
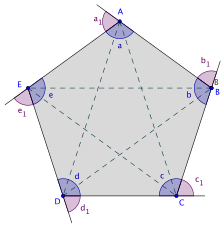
Exemplo[editar | editar código-fonte]
O polígono na figura ao lado possui:
- vértices
- lados e
- ângulos internos
- diagonais e
- ângulos externos e
Perímetro e Área[editar | editar código-fonte]
O perímetro de um polígono é a soma das medidas de seus lados. Sua área é a medida da região poligonal definida pelo polígono.
Classificação[editar | editar código-fonte]

Quanto à linha poligonal[editar | editar código-fonte]
Um polígono pode ser classificado em simples, quando sua linha poligonal associada é simples, ou não-simples (ou complexo), quando sua linha poligonal tem cruzamentos entre seus segmentos (conjunto intersecção não-nulo).[5]
Quanto à região poligonal[editar | editar código-fonte]
Um polígono simples é dito ser convexo quando toda reta determinada por dois de seus vértices consecutivos faz com que todos os demais vértices estejam num mesmo semiplano determinado por ela. Um polígono que não é convexo é dito ser côncavo.[5] Polígonos estrelados são polígonos complexos cujas intersecções de segmentos são equidistantes entre si.[6]
Quanto à congruência[editar | editar código-fonte]
Um polígono é dito ser equilátero quando todos os seus lados são congruentes. Similarmente, é dito ser equiângulo quando todos os seus ângulos são congruentes. Polígonos convexos equiláteros e equiângulos são chamados de polígonos regulares.
Quanto ao número de lados[editar | editar código-fonte]
Os polígonos também são classificados quanto ao número de lados. Em geral, um polígono de lados é chamado de -látero. Entretanto, comumente empregam-se as seguintes nomenclaturas:[5]
| Lados | Nome | Lados | Nome | Lados | Nome |
|---|---|---|---|---|---|
| 1 | não existe | 11 | undecágono | ... | ... |
| 2 | não existe | 12 | dodecágono | ||
| 3 | triângulo ou trilátero | 13 | tridecágono | 30 | triacontágono |
| 4 | quadrilátero | 14 | tetradecágono | 40 | tetracontágono |
| 5 | pentágono | 15 | pentadecágono | 50 | pentacontágono |
| 6 | hexágono | 16 | hexadecágono | 60 | hexacontágono |
| 7 | heptágono | 17 | heptadecágono | 70 | heptacontágono |
| 8 | octógono | 18 | octodecágono | 80 | octacontágono |
| 9 | eneágono | 19 | eneadecágono | 90 | eneacontágono |
| 10 | decágono | 20 | icoságono | 100 | hectágono |
Nomenclatura para polígonos com muitos lados[editar | editar código-fonte]
Para se construir o nome de um polígono com mais de 20 lados e menos de 100 lados, basta se combinar os prefixos e os sufixos a seguir:[7]
| Dezenas | e | Unidades | sufixo | ||
|---|---|---|---|---|---|
| -cai- | 1 | -ena- | -gono | ||
| 20 | icosi- | 2 | -di- | ||
| 30 | triaconta- | 3 | -tri- | ||
| 40 | tetraconta- | 4 | -tetra- | ||
| 50 | pentaconta- | 5 | -penta- | ||
| 60 | hexaconta- | 6 | -hexa- | ||
| 70 | heptaconta- | 7 | -hepta- | ||
| 80 | octaconta- | 8 | -octa- | ||
| 90 | eneaconta- | 9 | -enea- | ||
Exemplo 1[editar | editar código-fonte]
Um polígono de 42 lados deve ser nomeado da seguinte maneira:
| Dezenas | e | Unidades | sufixo | nome completo do polígono |
|---|---|---|---|---|
| tetraconta- | -cai- | -di- | -gono | tetracontacaidígono |
Exemplo 2[editar | editar código-fonte]
Um polígono de 50 lados da seguinte forma:
| Dezenas | e | Unidades | sufixo | nome completo do polígono |
|---|---|---|---|---|
| pentaconta- | -gono | pentacontágono | ||
Alguns polígonos possuem nomes alternativos, como o miriágono (10.000 lados).[8]
Propriedades[editar | editar código-fonte]
Podemos observar uma série de relações entre os diversos elementos de um polígono.[5] Aqui, apresentamos algumas destas propriedades.
Vértices e lados[editar | editar código-fonte]
O número de lados e o número de ângulos de um polígono é igual ao seu número de vértices.
Diagonais[editar | editar código-fonte]
- De cada vértice de um polígono de lados, saem diagonais. Com efeito, um polígono de lados tem vértices. De um dado vértice formamos segmentos de reta com cada um dos outros vértices. Agora, observamos que dois destes segmentos são lados do polígono, portanto, de cada vértice partem diagonais.
- O número de diagonais de um polígono -látero é: Com efeito, a combinação de seus vértices dois a dois fornece o número total de segmentos de reta que podem ser construídos usando todos os seus vértices. Deste número, são lados do polígono e o restante são diagonais, i.e.:
- Em um polígono convexo de lados, o número de triângulos formados por diagonais que saem de cada vértice é dado por De fato, diagonais partem de cada vértice determinando, com os lados do polígono, triângulos.
Ângulos[editar | editar código-fonte]
- A soma das medidas dos ângulos internos de um polígono convexo de lados é dada por: Com efeito, as diagonais que partem de um dado vértice formam triângulos. Observamos que é igual a soma dos ângulos internos destes triângulos, i.e.
- A soma das medidas dos ângulos externos de um polígono convexo de lados é igual a Com efeito, sejam e os respectivos ângulos interno e externo do -ésimo vértice de um polígono -látero. Por definição, temos para todo Daí, segue que: donde, vemos que
- A medida do ângulo interno de um polígono regular de lados é dada por:
- A medida do ângulo externo de um polígono regular de lados é dada por:
- A soma das medidas dos ângulos centrais de um polígono regular de lados () é igual a
- A medida do ângulo central de um polígono regular de lados () é dada por:
Mitologia[editar | editar código-fonte]
Segundo Eudoxo, citado por Plutarco, os pitagóricos associavam cada polígono a um (ou mais) deuses. O triângulo pertencia a Hades, Dionísio e Ares, o quadrilátero a Reia, Afrodite, Deméter, Héstia e Hera, o dodecágono a Zeus e o polígono de 56 lados à criatura demoníaca Tifão.[9]
Ver também[editar | editar código-fonte]
Referências
- ↑ «Dicionário Priberam da Língua Portuguesa: polígono». Priberam Informática. Consultado em 3 de dezembro de 2014
- ↑ Euclides, Os Elementos, Livro I, Definição 23 [em linha]
- ↑ Romirys Cavalcante. «O que é uma linha poligonal?». Consultado em 26 de março de 2019
- ↑ Victor G. Ganzha, Evgenii V. Vorozhtsov. Computer-Aided Analysis of Difference Schemes for Partial Differential Equations. [S.l.]: John Wiley & Sons. ISBN 9781118030851
- ↑ a b c d e f g Dolce, Osvaldo (2013). Fundamentos de Matemática Elementar 9 ed. [S.l.]: Atual. ISBN 9788535716863
- ↑ David Terr, Eric W. Weisstein. «Concave Polygon». MathWorld - A Wolfram Web Resource. Consultado em 26 de março de 2019
- ↑ R. S. Schaeffer. «Naming Polygons». Kutztown University. Consultado em 26 de março de 2019
- ↑ http://mathworld.wolfram.com/Myriagon.html
- ↑ Eudoxo, citado por Plutarco, Moralia, Ísis e Osíris, 30 [em linha]





































































