Congruência (geometria)
Esta página ou seção foi marcada para revisão devido a incoerências ou dados de confiabilidade duvidosa. (Fevereiro de 2011) |
As referências deste artigo necessitam de formatação. (Abril de 2013) |

A congruência é um conceito geométrico. Em geometria, duas figuras são congruentes se elas possuem a mesma forma e tamanho. Mais formalmente, dois conjuntos de pontos geométricos são ditos “congruentes” se, e somente se, um pode ser transformado no outro por isometria, ou seja, uma combinação de translações, rotações e reflexões. O conceito associado de similaridade admite uma mudança no tamanho entre duas figuras similares.
Dois ângulos são congruentes se, sobrepostos um sobre o outro, todos os seus elementos coincidem. Nos paralelogramos, os lados paralelos são congruentes, e os dois ângulos opostos pelo vértice são sempre congruentes. Num triângulo equilátero, todos os lados e ângulos são congruentes; nos triângulos isósceles, apenas os lados iguais e os ângulos da base são congruentes.
Definição de congruência em geometria analítica[editar | editar código-fonte]
Em um sistema euclidiano, o conceito de congruência é fundamental: é equivalente ao conceito de igualdade entre números. Em geometria analítica, a congruência pode ser definida intuitivamente da seguinte forma: o mapeamento de figuras em um sistema de coordenadas cartesianas são congruentes se e somente se para quaisquer dois pontos do primeiro mapeamento, a distância euclidiana entre eles é igual à distância Euclideana entre os pontos correspondentes no segundo mapeamento.
Uma definição mais formal pode ser dada por: dois subconjuntos “A” e “B” do espaço euclidiano Rn são chamados congruentes se existir uma isometria f : Rn → Rn (um elemento do grupo euclidiano E(n)) tal que f(A) = B. Congruência é uma relação de equivalência.
Congruência de segmentos de reta[editar | editar código-fonte]
Dois segmentos de reta são congruentes quando possuem o mesmo comprimento.
Congruência de ângulos[editar | editar código-fonte]
Dois ângulos são congruentes quando possuem a mesma medida ou "abertura".
Congruência de triângulos[editar | editar código-fonte]
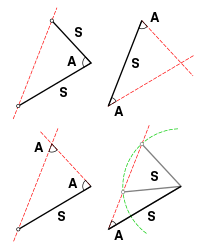
Dois triângulos são congruentes se seus lados correspondentes forem congruentes e seus ângulos correspondentes.
Se o triângulo ABC é congruente com o triângulo DEF, a relação pode ser escrita matematicamente como:
Em muitos casos, é suficiente estabelecer a igualdade entre três partes correspondentes e utilizar um dos seguintes resultados para deduzir a congruência de dois triângulos:
Determinando a congruência[editar | editar código-fonte]
A evidência da congruência entre dois triângulos no espaço Euclideano pode ser obtida através das seguintes comparações:[1]
- LAL (Lado-Ângulo-Lado): se dois lados dos dois triângulos forem congruentes e o ângulo entre estes lados for congruente, então os triângulos são congruentes.
- LLL (Lado-Lado-Lado): Se os dois triângulos apresentarem os três lados congruentes, então os triângulos são congruentes .
- ALA (Ângulo-Lado -Ângulo): Se dois triângulos possuem um lado e dois ângulos adjacentes a este lado respectivamente congruentes, então os triângulos são congruentes.
- AAL (Ângulo-Ângulo-Lado): Se dois triângulos possuirem um lado congruente, o ângulo oposto a este lado e o ângulo adjacente ao lado congruentes, então os triângulos são congruentes.
- RHL (Ângulo reto-Hipotenusa-Lado): Se dois triângulos retângulos possuírem hipotenusas congruentes e um cateto congruente, então os triângulos são congruentes.
Referências
- ↑ Congruência e Semelhança de Triângulos. Brasil escola.

