Octógono
| Octógono | |
|---|---|
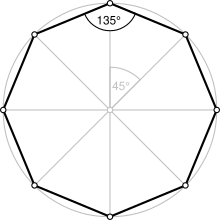 Octógono regular | |
| Tipo | Polígono regular |
| Arestas e Vértices | 8 |
| Símbolo de Schläfli | {8} t{4} |
| Diagrama de Coxeter | |
| Grupo de simetria | Simetria diédrica (D8) |
| Área | (sendo a = comprimento da aresta) |
| Ângulo interno (graus) | 135° |
| Propriedades | convexo, cíclico, equilateral, isogonal |
Em geometria, o octógono é um polígono com oito lados (e portanto oito ângulos internos, oito vértices e oito ângulos externos).[1]
Octógono regular[editar | editar código-fonte]
Um octógono regular tem todos os lados de mesmo tamanho e todos os ângulos com a mesma medida.
Construção de um octógono regular com régua e compasso[editar | editar código-fonte]

Área de um octógono regular[editar | editar código-fonte]
A área de um octógono regular de lado 'a' é
Sabendo o comprimento 'm' do apótema, e considerando o octógono composto por 8 triângulos isósceles, podemos recorrer a uma fórmula mais simples
Medida dos ângulos internos[editar | editar código-fonte]
Logo:
Então:
Daí conclui-se que a medida do ângulo interno de um octógono regular é 135.
Soma dos ângulos internos[editar | editar código-fonte]
Daí conclui-se que a soma dos ângulos internos de um octógono regular é 1080.
Medidas dos ângulos externos[editar | editar código-fonte]
Logo:
Daí conclui-se que a medida do ângulo externo de um octógono regular é 45.
Medida do ângulo central[editar | editar código-fonte]
Então:
Assim, conclui-se que a medida do ângulo central de um octógono regular é 45.
Número de diagonais[editar | editar código-fonte]
Então:
Logo:
Então:
Então, conclui-se que o número de diagonais de um octógono regular é 20.
Ver também[editar | editar código-fonte]
Referências
- ↑ «significados.com.br - Significado de Octógono». www.significados.com.br
















