Lógica difusa
A lógica difusa ou lógica fuzzy é a forma de lógica multivalorada, na qual os valores verdade das variáveis podem ser qualquer número real entre 0 (correspondente ao valor falso) e 1 (correspondente ao valor verdadeiro), diferentemente do que se verifica na lógica booliana (também chamada, às vezes, lógica nítida), segundo a qual os valores lógicos podem ser apenas 0 ou 1.[1]
A lógica difusa foi estendida para lidar com o conceito de verdade parcial, objetivando imitar o raciocínio humano em que o valor verdade situa-se entre o completamente verdadeiro e o completamente falso. Além disso, quando variáveis linguísticas são usadas, esses graus podem ser manipulados por funções especificas.[2]
O termo lógica difusa foi introduzido em 1965 com a proposta da teoria de conjuntos difusos por Lotfi A. Zadeh.[3][4] A lógica difusa tem sido aplicada em várias áreas, desde a teoria do controle à inteligência artificial. A lógica difusa tem sido no entanto estudada desde meados da década de 1920, como lógica infinito-valorada, por Łukasiewicz e Tarski.[5]
As implementações da lógica difusa permitem que estados indeterminados possam ser tratados por dispositivos eletrônicos, aplicação bastante frequente em controle não-linear de processos industriais. Deste modo, é possível avaliar conceitos não quantificáveis. Casos práticos: avaliar a temperatura de uma caldeira (quente, morno, médio, etc.), o sentimento de felicidade (radiante, feliz, apático, triste, etc.), a veracidade de um argumento (corretíssimo, correto, contra-argumentativo, incoerente, falso, totalmente errôneo, etc.)
Muitos pesquisadores de versões booleinas de lógica não aceitam a lógica difusa como uma verdadeira lógica, no sentido em que aceitam, por exemplo, a lógica modal. Isso pode ser associado a diferentes fatos, entre eles o de que muitos modelos permitem soluções aproximadas, que não correspondem a uma "verdade" lógica.
Visão geral[editar | editar código-fonte]
A lógica clássica apenas permite proposições tendo os valores de verdadeiro ou falso. Por exemplo, a noção de que 1+1 = 2 é uma verdade matemática absoluta imutável. Entretanto, existem certas proposições com respostas variáveis, tais como pedir a várias pessoas para identificarem uma cor. A noção de verdade não cai em esquecimento, mas um meio de representar e raciocinar sobre um conhecimento parcial é concedido, pela agregação de todos os resultados possíveis em um espectro dimensional.
Tanto graus de verdade como probabilidades estão compreendidos entre 0 e 1 e consequentemente pode parecer similar no começo. Por exemplo, imagine um copo de 100 ml contendo 30 ml de água. Então podemos considerar dois conceitos: cheio e vazio. O significado de cada pode ser representado por um conjunto difuso. Então, uma pessoa pode definir o copo como 70% vazio e 30% cheio. Note que o conceito de vazio seria subjetivo e dependeria do observador. Outro observador pode, igualmente, criar uma função onde o copo seria considerado cheio para todos os valores acima de 50 ml. É essencial perceber que a lógica difusa utiliza-se de graus de verdade como um modelo matemático do fenômeno de vagueza enquanto probabilidade é um modelo matemático de ignorância.
Aplicando valores verdade[editar | editar código-fonte]
Uma aplicação básica pode caracterizar vários subcontradomínios de uma variável contínua. Por exemplo, uma medição de temperatura para Freios ABS pode ter várias funções de filiação separadas definindo alcances de temperatura particulares necessários para controlar os freios corretamente. Cada função mapeia o mesmo valor temperatura para um valor verdade entre 0 e 1. Esses valores verdade podem então ser usados para determinar como os freios devem ser controlados.
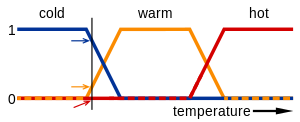
Nessa imagem, os significados das expressões frio (cold), morno (warm), e quente (hot) são representados por funções que mapeiam a escala de temperatura. Um ponto nessa escala tem três "valores-verdade" — um para cada uma das funções. A linha vertical na imagem representa uma temperatura particular que três setas (valores-verdade) medem. Como a seta vermelha aponta para zero, essa temperatura pode ser interpretada como "não quente". A seta laranja (apontando para 0,2) pode ser descrita como "levemente morno" e a seta azul (apontando para 0,8) "relativamente frio".
Variáveis Linguísticas[editar | editar código-fonte]
Enquanto variáveis na matemática usualmente tomam valores numéricos, nas aplicações da lógica difusa, as não numéricas são frequentemente usadas para facilitar as expressões de regras e fatos.[6]
Uma variável linguística tal como idade pode ter um valor como jovem ou seu antônimo velho. No entanto, a grande utilidade das variáveis linguísticas é que elas podem ser modificadas via limites linguísticos aplicados a termos primários. Esses limites linguísticos podem ser associados a certas funções.
Primeiras aplicações[editar | editar código-fonte]
Os japoneses foram os primeiros a utilizar a lógica difusa para aplicações práticas. A primeira aplicação notável foi em um Trem Bala em Sendai, na qual a lógica difusa possibilitou a melhora na economia, conforto e precisão do percurso.[7] Também foi usado no reconhecimento de símbolos manuscritos em computadores de bolso da Sony; na assistência de voo para helicópteros; no controle de sistemas metroviários, de forma a melhorar o conforto de direção, a precisão de parada e favorecer a economia de energia; melhoria do consumo de combustível para carros; controles de lavadoras por um único botão; controle automático de motores de aspiradores de pó, com reconhecimento das condições da superfície e de degradação do solo; e sistemas de previsão para reconhecimento antecipado de terremotos através do Instituto de Sismologia no Japão.[8]
Noções básicas[editar | editar código-fonte]
Na lógica proposicional, a cada proposição p associamos um entre dois valores possíveis: verdadeiro ou falso. É comum que sejam escolhidos valores numéricos como 1 para representar o verdadeiro e 0 para representar o falso.
Um modelo difuso simples é construído associando-se um valor μ(p) a uma proposição p, indicando o grau de veracidade dessa proposição, sendo que μ(x) é uma função (arbitrária) cujo conjunto imagem está entre 0 e 1 (ou 0% e 100%). Se exige pouco dessa funcional: caso p seja verdade, deve estar associado ao valor 100%, caso p seja falso deve ser associado ao valor 0%. Dessa forma, a lógica difusa estende a lógica booliana, pois ao invés de permitir só dois valores (1 e 0) permite uma gama infinita de valores.
Da mesma forma que são estendidos os valores possíveis das proposições, também devem ser estendidos os operadores, como NÃO, E e OU. Porém, ao estender esses operadores, devemos manter certas propriedades, entre elas a compatibilidade com a versão booliana da lógica. Assim, um operador NÃO difuso, ao ser aplicado sobre o valor de uma proposição difusa que seja 0 ou 1, deve devolver o mesmo valor que um operador NÃO retornaria na lógica booliana.
Existem uma ampla gama de funções que podem ser utilizadas como NÃO difusa, E difusa e OU difusa, tendo sido aplicadas a vários sistemas, porém as que contém mais propriedades desejáveis e que simultaneamente são bastante fáceis de utilizar são:
- NÃO-difuso(x) = 1 - x
- E-difuso(x,y) = Mínimo(x,y)
- OU-difuso(x,y) = Máximo(x,y)
Utilizando esse modelo, podemos construir o seguinte exemplo:
Suponha que desejássemos representar de forma difusa a altura de Alice (1,65 m), Bob (1,75 m), Carlos(2,0m) e Denise(1,45 m). Nossas proposições serão da forma "X é alto", e serão:
- A = Alice é alta, μ(A) = 0,55
- B = Bob é alto, μ(B) = 0,75
- C = Carlos é alto, μ(C) = 1
- D = Denise é alta, μ(D) = 0
Usando os operadores acima descritos, podemos escrever afirmações como:
- Carlos não é alto, NÃO(C), μ(NÃO(C)) = 1-μ(C) = 0
- Bob não é alto, NÃO(B), μ(NÃO(B)) = 1-μ(B)= 0,25
- Denise é alta e Alice é Alta, D e A, μ(D e A) = mínimo(μ(D),μ(A)) = 0
A lógica está claramente associada a teoria dos conjuntos. Cada afirmação (do tipo "Carlos é alto") representa na verdade o grau de pertinência de Carlos ao conjunto de pessoas altas. Isso permite que conjuntos como "alto" e "baixo" sejam tratados de forma separadas e afirmações como "Carlos é alto 0,75" e "Carlos é baixo 0,50" sejam válidas simultaneamente, ao contrário do que seria esperado em um modelo nítido. Esse tipo de afirmação é facilmente encontrada na descrição, por humanos, na forma como entendem certo conceito, e a lógica difusa é uma ótima forma de tratar essa forma de incerteza.
Inferência difusa[editar | editar código-fonte]
Fazer uma inferência difusa significa aplicar regras do tipo SE X ENTÃO Y de forma que X e Y, e a própria sentença, sejam noções difusas.
Dessa forma, se torna mais fácil interpretar matematicamente e implementar sistemas a partir do conhecimento humano, como em: SE A TEMPERATURA É ALTA E A PRESSÃO É ALTA ENTÃO O FLUXO DE COMBUSTÍVEL DEVE SER PEQUENO.
É importante notar que no caso acima, uma versão de uso corrente da lógica difusa, a regra é igual a uma regra nítida que seria usada em um sistema especialista. Porém, os conjuntos (ALTO, MÉDIO e BAIXO para temperatura, por exemplo) permitem graus de pertinência, onde uma temperatura pode ter algum grau em todos os conjuntos, enquanto em um sistema nítido, apenas um valor seria possível.
Assim, em sistemas difusos, com um conjunto de regras, várias regras aparentemente contraditórias são válidas simultaneamente, possuindo ainda um grau de validade. A solução final é obtida por meio da agregação dos resultados por meio de alguma operação matemática, como o cálculo do centro de massa da resposta obtida.
No caso da inferência, para cada conjunto de operações básicas NÃO, E e OU escolhidos, são possíveis várias versões da implicação. Isso porque, na lógica nítida, AB (A implica B) é equivalente a várias sentenças.
Outra forma de inferência difusa é aplicar regras como o modus ponens e modus tollens. Isso permite várias variações. Em uma delas, sabendo que "A implica B" de forma nítida, e tendo apenas um valor difuso de A, é possível calcular o valor de B.
Conjuntos difusos[editar | editar código-fonte]
Normalmente, o uso da lógica difusa está associado ao uso de conjuntos nebulosos.
Um conjunto nebuloso estende o conceito de conjunto permitindo que um elemento passa a ter um grau de pertinência variando entre 0 e 1, ao invés de pertencer ou não ao conjunto como na teoria de conjuntos tradicional.
Veja que o princípio é o mesmo aplicado a lógica difusa, onde o grau de veracidade pode passar a variar entre 0 e 1.
Para cada conjunto, então, é criada uma função de pertinência, que indica o grau de pertinência de seus elementos. Normalmente, essa função é criada de forma a representar algum conceito impreciso, como "ser alto".
Raciocínio difuso[editar | editar código-fonte]
O raciocínio difuso também conhecido como raciocínio aproximado pode ser dividido em 5 etapas.
- Transformação das variáveis do problema em valores difusos, ou difusificação
- Aplicação dos operadores difusos
- Aplicação da implicação
- Combinação de todas as saídas difusas possíveis
- Transformação do resultado difuso em um resultado nítido, a difusificação.
No primeiro passo, para cada valor de entrada associamos uma função de pertinência, que permite obter o grau de verdade da proposição.
- Determinar o grau de pertinência de cada conjunto (proposição);
- Limitar o valor da entrada entre 0 e 1;
O segundo passo é aplicar os operadores difusos, assim como os operadores da lógica nítida. Os operadores usados na lógica difusa são AND e OR, conhecidos como operadores de relação. Na lógica difusa são utilizados para definir o grau máximo e mínimo de pertinência do conjunto.
O terceiro passo é aplicar o operador de implicação, usado para definir o peso no resultado e remodelar a função, ou seja, o terceiro consiste em criar a hipótese de implicação. Como no exemplo abaixo:
- Serviço é excelente OU atendimento é rápido ENTÃO pagamento é alto.
No quarto passo ocorre a combinação de todas as saídas em um único conjunto difuso, algo semelhante ao processo de união e intersecção, na teoria dos conjuntos abruptos.
O quinto e último passo no processo do raciocínio difuso é a difusificação, que consiste em retornar os valores, obter um valor numérico dentro da faixa estipulada pela lógica difusa.
Um exemplo simples que demonstra o processo de pertinência do raciocínio difuso seria. Se A é identificado como ‘o tomate está vermelho’ e B como ‘o tomate está maduro’, então se é verdade que ‘o tomate está vermelho’, é também verdade que ‘o tomate está maduro’. Essa seria um exemplo pensado na lógica tradicional onde:
- Fato: x é A;
- Regra: se x é A então y é B;
- Conclusão: y é B
Esta regra aplica um conceito aproximado. Porem se pensarmos desta forma: se nós temos a mesma regra de implicação se o tomate está vermelho, então ele está maduro e nós sabemos que o tomate está mais ou menos vermelho, então nós podemos inferir que o tomate está mais ou menos maduro. Ou seja:
- Fato: x é A’ (quase A)
- Regra: se x é A então y é B
- Conclusão: y é B’ (quase B)
Este conceito de difusificação funciona da seguinte forma se A’ está próximo de A (situação inicial) e B’ está próximo de B (inicial). A, A’, B e B’ fazem parte do conjunto universo, chegando assim ao paradigma do raciocínio difuso, também chamado de modus ponens generalizado.
Análise lógica[editar | editar código-fonte]
Na lógica matemática, existem vários sistemas formais de lógica difusa ou "lógíca fuzzy", a maioria deles pertencem a chamada t-norma da lógica difusa.
Lógica difusa proposicional[editar | editar código-fonte]
As lógicas difusas proposicionais mais importantes são:
- Lógica difusa proposicional baseado em t-norma monoidal ou Monoidal t-norm-based propositional fuzzy logic (MTL) é uma axiomatização da lógica onde conjunção é definida por uma t-norma esquerda contínua e implicação é definida como o resíduo da t-norma. Seus modelos correspondem a álgebras MT que são grades de comutativos pré-lineares limitados integrais residuados.
- Lógica difusa proposicional básica ou Basic propositional fuzzy logic (BL) é uma extensão da lógica MTL onde conjunção é definida por uma t-norma contínua, e implicação é também definida como o resíduo da t-norma. Seu modelo corresponde a álgebras BL.
- Lógica difusa Łukasiewicz é a extensão da Lógica difusa BL onde a conjunção padrão é a t-norma Łukasiewicz. Tem o axioma da lógica difusa básica mais um axioma de dupla negação, e seus modelos correspondem a álgebras MV.
- Lógica difusa de Gödel é a extensão da lógica difusa básica BL onde conjunção é a t-norma Gödel. Tem os axiomas de BL mais um axioma de idempotência de conjunção, e seus modelos são chamados de álgebras G.
- Lógica difusa do produto é a extensão da lógica difusa básica BL onde conjunção é t-norma produto. Tem os axiomas BL mais outro axioma para cancelatividade da conjunção, e seus modelos são chamados de produtos algébricos.
- Lógica difusa com sintaxe avaliada (Ás vezes também chamada de Lógica de Pavelkas), denotada por EVŁ, é uma generalização mais profunda da lógica difusa matemática. Enquanto os acima citados tipos de lógica difusa tem sintaxe tradicional e semântica de muitos valores, em EVŁ é avaliada também a sintaxe. Isso significa que cada fórmula tem uma avaliação. Axiomatização da EVŁ da Lógica difusa Łukasiewicz. Uma generalização do teorema da completude clássica de Gödel pode ser provado em EVŁ.
Lógica difusa de predicados[editar | editar código-fonte]
Esses estendem-se as lógicas difusas acima citadas adicionando quantificadores existenciais e universais de uma maneira similar ao jeito que a lógica de predicados é criada da lógica proposicional. As semânticas do quantificador universal in t-normas da lógica difusa é o infímo dos graus de verdade das intâncias da subfórmula quantificada. Já o existencial é o supremo desses graus.
Problemas de decidibilidade para lógica difusa[editar | editar código-fonte]
As noções de um "subconjunto decidível" e "subconjunto recursivamente enumerável" são básicos para matemática clássica e lógica clássica. Portanto a questão de uma extensão adequada desses conceitos para a teoria de conjuntos difusos surge. Uma primeira proposta em tal direção, foi feita por E.S. Santos pela noção de Máquina de Turing difusa, Algoritmo de difusão normal de Markov, e programa difuso. Sucessivamente, L. Biacino e G. Gerla argumentaram que as definições propostas são um pouco questionáveis e portanto eles propuseram as seguintes. Denotada por Ü o conjunto de números racionais em [0,1]. Então um subconjunto difuso s : S [0,1] de um conjunto S é recursivamente enumerável se um mapa recursivo h : S×N Ü existe desse jeito, para todo x em S, a função h(x,n) é aumentada com respeito a n e s(x) = lim h(x,n). Nós dizemos s é dicidível se tanto s e seu complemento –s são recursivamente enumeráveis. Uma extensão de tal teoria para o caso geral de L-subconjuntos é possível (veja Gerla 2006). As definições propostas são bem relacionadas com a lógica difusa. De fato, o seguinte teorema é verdadeiro (Dado que o aparto de dedução da considerada lógica difusa, satisfaça alguma óbvia propriedade de efetividade).
Ver também[editar | editar código-fonte]
Referências
- ↑ LANZILLOTTI, R.S. Lógica Fuzzy: uma Abordagem Para Reconhecimento de Padrão. São Paulo: Paco Editorial, 2014.
- ↑ Ahlawat, Nishant, Ashu Gautam, and Nidhi Sharma (International Research Publications House 2014) "Use of Logic Gates to Make Edge Avoider Robot." International Journal of Information & Computation Technology. Volume 4, # 6; p. 630. ISSN 0974-2239
- ↑ «Fuzzy Logic». Stanford Encyclopedia of Philosophy. Bryant University. 23 de julho de 2006. Consultado em 30 de setembro de 2008
- ↑ Zadeh, L.A. (1965). «Fuzzy sets». Information and Control. 8 (3): 338–353. doi:10.1016/s0019-9958(65)90241-x
- ↑ Pelletier, Francis Jeffry (2000). «Review of Metamathematics of fuzzy logics» (PDF). The Bulletin of Symbolic Logic. 6 (3): 342–346. JSTOR 421060. doi:10.2307/421060. Cópia arquivada (PDF) em 3 de março de 2016
- ↑ Zadeh, L. A.; et al. (1996). Fuzzy Sets, Fuzzy Logic, Fuzzy Systems. [S.l.]: World Scientific Press. ISBN 978-981-02-2421-9
- ↑ Kosko, Bart (1º de junho de 1994). «Fuzzy Thinking: The New Science of Fuzzy Logic». Hyperion
- ↑ Bansod, Nitin A; Kulkarni, Marshall; Patil, S.H. (2005). «Soft Computing- A Fuzzy Logic Approach». In: Bharati Vidyapeeth College of Engineering. Soft Computing. [S.l.]: Allied Publishers. 73 páginas. ISBN 978-81-7764-632-0
Bibliografia[editar | editar código-fonte]
- Novák, V., Perfilieva, I. and Močkoř, J. (1999) Mathematical principles of fuzzy logic Dodrecht: Kluwer Academic. ISBN 0-7923-8595-0
- Ahlawat, Nishant, Ashu Gautam, and Nidhi Sharma (International Research Publications House 2014) "Use of Logic Gates to Make Edge Avoider Robot." International Journal of Information & Computation Technology (Volume 4, Issue 6; page 630) ISSN 0974-2239
- "Fuzzy Logic". Stanford Encyclopedia of Philosophy. Stanford University. 2006-07-23. Retrieved 2008-09-30
- W. Pedrycz and F. Gomide; “Fuzzy Systems Engineering : Toward Human-Centric Computing”; Wiley/IEEE Press, 2007 ; ISBN 978-0-471-78857-7
- C. J. Harris, C. G. Moore & M. Brown; “Intelligent control : Aspects of Fuzzy Logic and Neural Nets”; World Scientific, 1993; ISBN 981-02-1042-6
- Kosko, Bart; “Neural networks and fuzzy systems: a dynamical systems approach to machine intelligence”; Prentice-Hall International, 1992; ISBN 0-13-612334-1
- Earl Cox; “The Fuzzy Systems Handbook : a Practitioner's Guide to Building, Using and Maintaining Fuzzy Systems”; Professional, 1994 ; ISBN 0-12-194270-8

