Sequência de Fibonacci

Na matemática, os Números de Fibonacci são uma seqüência (sucessão, em Portugal) definida como recursiva pela fórmula abaixo:

$F(n)=\left\{{\begin{matrix}0\,,\qquad \qquad \qquad \quad \,\ \ \,&&{\mbox{se }}n=0\,;\ \ \\1,\qquad \qquad \qquad \qquad \,&&{\mbox{se }}n=1;\ \ \,\\F(n-1)+F(n-2)&&{\mbox{outros casos.}}\end{matrix}}\right.$

Na prática: você começa com 1 e 1, e então produz o próximo número de Fibonacci somando os dois anteriores para formar o próximo. Os primeiros Números de Fibonacci (sequência A000045 na OEIS) para n = 0, 1,… são

0,1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946…

Esta seqüência foi descrita primeiramente por Leonardo de Pisa, também conhecido como Fibonacci (Dc. 1200), para descrever o crescimento de uma população de coelhos. Os números descrevem o número de casais em uma população de coelhos depois de n meses se for suposto que:

• no primeiro mês nasce apenas um casal,
• casais amadurecem sexualmente (e reproduzem-se) apenas após o segundo mês de vida,
• não há problemas genéticos no cruzamento consangüíneo,
• todos os meses, cada casal fértil dá a luz a um novo casal, e
• os coelhos nunca morrem.

O termo seqüência de Fibonacci é também aplicado mais genericamente a qualquer função g onde g(n + 2) = g(n) + g(n + 1). Estas funções são precisamente as de formato g(n) = aF(n) + bF(n + 1) para alguns números a e b, então as seqüências de Fibonacci formam um espaço vetorial com as funções F(n) e F(n + 1) como base.

Em particular, a seqüência de Fibonacci com F(1) = 1 e Ver artigo principal: Sequência de Fibonacci F(2) = 3 é conhecida como os números de Lucas. A importância dos números de Lucas L(n) reside no fato deles gerarem a Proporção áurea para as enésimas potências:

$\left({\frac {1}{2}}\left(1+{\sqrt {5}}\right)\right)^{n}={\frac {1}{2}}\left(L(n)+F(n){\sqrt {5}}\right)$

Os números de Lucas se relacionam com os de Fibonacci pela fórmula:

$L(n)=F(n-1)+F(n+1)$

Com esta fórmula podemos montar a Seqüência de Fibonacci e descobrir, por exemplo, quantos coelhos foram gerados no sexto mês, basta aplicar a fórmula descrita acima até chegar ao ponto inicial de 1 e 1.

Como mostra a figura abaixo;

Uma grade preenchida com quadrados cujos lados são números de Fibonacci, formando sucessivamente retângulos cada vez maiores e tendentes à razão áurea

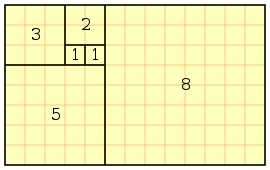
Ou seja, no sexto mês foram gerados 8 coelhos

F(6) = (F(6) - 1) + (F(6) - 2) = 5 e 4 → 8 ( Soma do Resultado de F(5) e F(4) )
F(5) = (F(5) - 1) + (F(5) - 2) = 4 e 3 → 5 ( Soma do Resultado de F(4) e F(3) )
F(4) = (F(4) - 1) + (F(4) - 2) = 3 e 2 → 3 ( Soma do Resultado de F(3) e F(2) )
F(3) = (F(3) - 1) + (F(3) - 2) = 2 e 1 → 2
F(2) = (F(2) - 1) + (F(2) - 2) = 1 e 0 → 1

e a primeira posição 1.

Note que a Seqüência de Fibonacci esta no resultado de cada posição; 1,1,2,3,5,8 …

Fórmula explícita

Conforme mencionado por Johannes Kepler, a taxa de crescimento dos números de Fibonacci, que é F(n + 1) /F(n), tende à Proporção áurea, denominada φ. Esta é a raiz positiva da equação de segundo grau x² − x − 1 = 0, então φ² = φ + 1. Se multiplicarmos ambos os lados por φⁿ, teremos φⁿ⁺² = φⁿ⁺¹ + φⁿ, então a função φⁿ é uma sequência de Fibonacci. É possível demonstrar que a raiz negativa da mesma equação, 1 − φ, tem as mesmas propriedades, então as duas funções φⁿ e (1 − φ)ⁿ formam outra base para o espaço.

Ajustando os coeficientes para obter os valores iniciais adequados F(0) = 0 e F(1) = 1, temos a fórmula de Binet

$F\left(n\right)={\frac {1}{\sqrt {5}}}\left\{\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{n}\right\}={\phi ^{n} \over {\sqrt {5}}}-{(1-\phi )^{n} \over {\sqrt {5}}}$

Este resultado também pode ser derivado utilizando-se a técnica de gerar funções, ou a técnica de resolver relações de multiplicação

Quando n tende a infinito, o segundo termo tende a zero, e os números de Fibonacci tendem à exponencial φⁿ/√5. O segundo termo já começa pequeno o suficiente para que os números de Fibonacci possam ser obtidos usando somente o primeiro termo arredondado para o inteiro mais próximo.

Calculando números de Fibonacci

Na prática não é conveniente calcular os números de Fibonacci usando potências da proporção áurea, a não ser para valores pequenos de n, já que os erros de arredondamento se acumulam e a precisão dos números de ponto flutuante normalmente não será suficiente.

A implementação direta da definição recursiva da sequência de Fibonacci também não é recomendável porque os mesmos valores são calculados muitas vezes (a não ser que a linguagem de programação guarde automaticamente os valores calculados nas chamadas anteriores da mesma função com o mesmo argumento). Por esse motivo, normalmente calcula-se os números de Fibonacci "de baixo para cima", começando com os dois valores 0 e 1, e depois repetidamente substituindo-se o primeiro número pelo segundo, e o segundo número pela soma dos dois anteriores.

Para argumentos muito grandes, quando utiliza-se um computador bignum, é mais fácil calcular os números de Fibonacci usando a seguinte equação matricial:

${\begin{bmatrix}1&1\\1&0\end{bmatrix}}^{n}={\begin{bmatrix}F\left(n+1\right)&F\left(n\right)\\F\left(n\right)&F\left(n-1\right)\end{bmatrix}}$

onde a potência de n é calculada elevando-se a matriz ao quadrado repetidas vezes.

Um exemplo de aplicação desta expressão matricial é na demonstração do teorema de Lamé sobre o algoritmo de Euclides para o cálculo do MDC. Veja por exemplo o capítulo Máximo divisor comum do Wikilivro de Teoria de números.

A seguir, um algoritmo desenvolvido em Java, o qual imprime o número de termos da sequência, determinado pela variável "x".

Representação da Série de Fibonacci na Molle Antonelliana em Turim, Itália.

Algoritmo em Java

Algoritmo Recursivo em Java

//Classe java
public class Fibonacci {

	public static int calcular(int n) {

		if (n == 0 || n == 1)
			return n;
		else
			return calcular(n - 1) + calcular(n - 2);
	}
}

// Impressão
public class Main {

	public static void main(String[] args) {

		for (int x = 1; x < 10; x++) {
			int y = Fibonacci.calcular(x);
			System.out.println("o Fibonacci de "+x+" é " + y);
		}

	}

}

Algoritmo Recursivo em Scheme

(define (fib n)
  (cond ((= n 0) 0)
        ((= n 1) 1)
        (else (+ (fib (- n 1)) (fib (- n 2))))))

Algoritmo Iterativo em Scheme

(define (fib n)
  (define (iter i p r)
    (if (= i n)
        r
        (iter (+ i 1) r (+ p r))))
  (cond ((= n 0) 0)
        ((= n 1) 1)
        (else (iter 2 1 1))))

Algoritmo em ECMAScript / JavaScript

/* Algoritmo Recursivo da Seqüência Fibonacci */
function fibonacci(i) {
    return i < 2 ? i : fibonacci(i - 1) + fibonacci(i - 2);
}
/* Chamando … */
for(i = 1; i < 10; i++) {
    alert(fibonacci(i));
}

Algoritmo recursivo em Python

Solução clássica usando recursividade.

# Função recursiva
def fibo(n):
    if n < 2:
        return n
    else:
        return fibo(n-1) + fibo(n-2)

for i in range(10):
    print fibo(i)

Algoritmo eficiente em Python

Solução em tempo linear com o uso de generators.

# Generator
def fib(n):
    c, n1, n2 = 0, 0, 1
    while c < n:
        yield n1
        n1, n2 = n2, n1 + n2
        c += 1

for x in fib(10):
  print x

<fib(n)>

       c,n1,n1,n2,n3,n6

Algoritmo em PHP

<?php
/* Algoritmo Recursivo da Seqüência Fibonacci */
function fibonacci($i) {
    return $i < 2 ? $i : fibonacci($i-1) + fibonacci($i-2);
}
/* Chamando … */
for($i=1;$i<10;$i++) {
    echo fibonacci($i)."\r\n";
}
?>

Algoritmo em Perl

# !/usr/bin/perl
use strict;
sub fibo {
  return $_[0] < 2 ? $_[0] : fibo($_[0]-1) + fibo($_[0]-2);
}
for (1..10){
  print fibo($_)."\n";
}

Modo mais eficiente :

# !/usr/bin/perl
use strict;
my ($a,$b)=(1,2);
print "$a\n$b\n";
for(1..100) {
  ($a,$b) = ($b,$a+$b);
  print "$b\n"
}

Algoritmo em C

int fibonacci(int n)
{
   if (n==0 || n==1) return n;
   return fibonacci(n-1) + fibonacci(n-2);
}

Algoritmo em Ruby

# Algoritmo Recursivo da Seqüência Fibonacci
def fib(n)
	return n if n<2
	fib(n-1)+fib(n-2)
end

# Chamando…
for i in (1..10)
	puts fib(i)
end

# Ou com memorização
fib = Hash.new{|hash, n| hash[n] = (n < 2) ? n : hash[n - 1] + hash[n - 2];};
(1..100).each do |i|
  puts fib[i]
end

Algoritmo em Shell Script (Zsh)

fibonacci() {
	local a c
	local -F1 b
	a=0 ; b=1
	print $a
	repeat $1
	do
		print "${b%.*}"
		c=$a
		a=$b
		((b = c + b))
	done
}

# Chamando…
fibonacci 10

Algoritmo em bc (comando Unix)

define void fibonacci(valor)
{
   auto x, y, z, i;
   
   x = 0;
   y = 1;
     
   x;
     
   while (i++ < valor) {
      y;
      z = x;
      x = y;
      y = z + y;
   }
}

Algoritmo em Pascal

program fibonacci (input,output);

var
	i,n,ni,ni1,ni2:longint;

begin
	writeln;

        writeln ('NÚMEROS DE FIBONACCI');

        writeln;

        write('Quantos termos de Fibonacci você quer calcular? ');
	read(n);
	ni:=1;
	ni1:=1;
	ni2:=0;
	
	for i:=1 to n do
		begin
			write(ni,' ');
			ni:=ni1+ni2;
			ni2:=ni1;
			ni1:=ni;
		end;
end.

Algoritmo em MATLAB

a=0;
b=1;
c=a+b;
N=0;
while N⇐0
    N=input('Defina limite da sequência fibonacci: ');
end
while c⇐N
    disp(num2str(c))
    a=b;
    b=c;
    c=a+b;
end

Algoritmo em Prompt Script (BAT)

@echo off
setlocal ENABLEDELAYEDEXPANSION
set /a e=1
set /a c2=0
set /a c3=1
:loop
set /a e=%e%+1
set /a f=%e%-1
set /a g=%e%-2
set /a c%e%=!c%f%!+!c%g%!
echo Fibonacci: !c%e%!
pause
goto loop

Algoritmo em PROLOG

fib(0, 1).
fib(1, 1).
fib(X, Y):- X > 1, X1 is X - 1, X2 is X - 2, fib(X1, Z), fib(X2, W), Y is W + Z.

Algoritmo em Tcl

proc fib {n} {
	if {$n < "2"} {
		return $n
	}
	return [expr [fib [expr $n - 1]] + [fib [expr $n - 2]]]
}

# Chamando
fib 10

Algoritmo em COBOL

*----------------------
 300-FIBONACCI SECTION.
*----------------------
     IF 999E-REG EQUAL 0
         MOVE PNULT TO FIB
     ELSE
         IF  999E-REG EQUAL 1
             MOVE ULT TO FIB
         ELSE
             MOVE 999E-REG TO GDA-POSICAO
             PERFORM 400-CALCULA UNTIL GDA-POSICAO EQUAL 1.
*---------------------------------------------------------------*
*
*--------------------
 400-CALCULA SECTION.
*--------------------
     COMPUTE FIB = ULT + PNULT.
     MOVE ULT TO PNULT.
     MOVE FIB TO ULT.
     SUBTRACT 1 FROM GDA-POSICAO.
*---------------------------------------------------------------*

Aplicações

Os números de Fibonacci são importantes para a análise em tempo real do algoritmo euclidiano, para determinar o máximo divisor comum de dois números inteiros.

Matiyasevich mostrou que os números de Fibonacci podem ser definidos por uma Equação diofantina, o que o levou à solução original do Décimo Problema de Hilbert.

Os números de Fibonacci aparecem na fórmula das diagonais de um triângulo de Pascal (veja coeficiente binomial).

Um uso interessante da seqüencia de Fibonacci é na conversão de milhas para quilômetros. Por exemplo, para saber aproximadamente a quantos quilômetros 5 milhas correspondem, pega-se o número de Fibonacci correspondendo ao número de milhas (5) e olha-se para o número seguinte (8). 5 milhas são aproximadamente 8 quilômetros. Esse método funciona porque, por coincidência, o fator de conversão entre milhas e quilômetros (1.609) é próximo de φ (1.618) (obviamente ele só é útil para aproximações bem grosseiras: além do factor de conversão ser diferente de φ, a série converge para φ).

Exemplo de sons Fibonacci

Em música os números de Fibonacci são utilizados para a afinação, tal como nas artes visuais, determinar proporções entre elementos formais. Um exemplo é a Música para Cordas, Percussão e Celesta de Béla Bartók.

Le Corbusier usou a seqüência de Fibonacci na construção do seu modulor, um sistema de proporções baseadas no corpo humano e aplicadas ao projeto de arquitetura.

Em The Wave Principal, Elliot defende a ideia que as flutuações do mercado seguem um padrão de crescimento e decrescimento que pode ser analisado segundo os números de Fibonacci, uma vez determinada a escala de observação. Defende que as relações entre picos e vales do gráfico da flutuação de bolsa tendem a seguir razões numéricas aproximadas das razões de dois números consecutivos da sequência de Fibonacci.

Teorias mais recentes, defendem que é possível encontrar relações “de ouro” entre os pontos de pico e os de vale, como no gráfico abaixo:

Se tomarmos o valor entre o início do ciclo e o primeiro pico, e o compararmos com o valor entre este pico e o pico máximo, encontraremos também o número de ouro. O ciclo, naturalmente, pode estar invertido, e os momentos de pico podem se tornar momentos de vale, e vice-versa.

Generalizações

Uma generalização da seqüência de Fibonacci são as Seqüências de Lucas. Um tipo pode ser definido assim:

U(0) = 0

U(1) = 1

U(n+2) = PU(n+1) − QU(n)

onde a seqüência normal de Fibonacci é o caso especial de P = 1 e Q = -1. Outro tipo de seqüência de Lucas começa com V(0) = 2, V(1) = P. Tais seqüências têm aplicações na Teoria de Números e na prova que um dado número é primo (primalidade).

Os polinômios de Fibonacci são outra generalização dos números de Fibonacci.

Identidades

F(n + 1) = F(n) + F(n − 1)

F(0) + F(1) + F(2) + … + F(n) = F(n + 2) − 1

F(1) + 2 F(2) + 3 F(3) + … + n F(n) = n F(n + 2) − F(n + 3) + 2

Podemos provar essas identidades usando diferentes métodos. Mas, entretanto, nós queremos demonstrar uma elegante prova para cada um de seus usos aqui. Particularmente, F(n) podem ser interpretados como o número de formas de adicionar 1's e 2's até n − 1, convencionando-se que F(0) = 0, significando que nenhuma soma irá adicionar até -1, e que F(1) = 1, significando que a soma 0 será "adicionada" até 0. Aqui a ordem dos números importa. Por exemplo, 1 + 2 e 2 + 1 são consideradas duas diferentes somas e são contadas duas vezes.

Prova da primeira identidade

Sem perda de generalidade, podemos assumir n ≥ 1. Então F(n + 1) conta o número de formas de somar 1's e 2's até n.

Quando a primeira parcela é 1, há F(n) formas de completar a contagem para n − 1; quando a primeira parcela é 2, há F(n − 1) formas de completar a contagem para n − 2. Portanto, no total, há F(n) + F(n − 1) formas de completar a contagem para n. $\Box$

ohlé?

Prova da segunda identidade

Contamos o número de formas de somar 1's e 2's até n + 1 de forma que pelo menos uma das parcelas é 2.

Como antes, há F(n + 2) formas de somar 1's e 2's até n + 1 quando n ≥ 0. Já que há apenas uma soma n + 1 que não usa nenhum 2, a saber 1 + … + 1 (n + 1 termos), subtraímos 1 de F(n + 2).

Equivalentemente, podemos considerar a primeira ocorrência de 2 como uma parcela.

Se, em uma soma, a primeira parcela é 2, então há F(n) formas de completar a contagem para n − 1. Se a segunda parcela é 2, mas a primeira é 1, então há F(n − 1) formas de completar a contagem para n − 2. Continuando este raciocínio iremos chegar à (n + 1)-ésima parcela. Se é 2, mas todas as n parcelas anteriores são 1's, então há F(0) formas de completar a contagem para 0. Se uma soma contém 2 como uma parcela, a primeira ocorrência de tal parcela deve tomar lugar entre a primeira e a (n + 1)-ésima posição. Portanto F(n) + F(n − 1) + … + F(0) dá a contagem desejada. $\Box$

Prova da terceira identidade

Essa identidade pode ser estabelecida em duas fases. Primeiro, contamos o número de formas de somar 1's e 2's até -1, 0, …, ou n + 1 tal que pelo menos uma das parcelas seja 2.

Pela nossa segunda igualdade, há F(n + 2) − 1 formas de somar até n + 1; F(n + 1) − 1 formas de somar até n; …; e, finalmente, F(2) − 1 formas de somar até 1.

Como F(1) − 1 = F(0) = 0 , podemos adicionar todos as somas n + 1 e aplicar a segunda igualdade novamente para obter:    [F(n + 2) − 1] + [F(n + 1) − 1] + … + [F(2) − 1]

= [F(n + 2) − 1] + [F(n + 1) − 1] + … + [F(2) − 1] + [F(1) − 1] + F(0)

= F(n + 2) + [F(n + 1) + … + F(1) + F(0)] − (n + 2)

= F(n + 2) + F(n + 3) − (n + 2).

Por outro lado , observamos a partir da segunda igualdadee que existem

• F(0) + F(1) + … + F(n − 1) + F(n) meios somando com n + 1;
• F(0) + F(1) + … + F(n − 1) meios somando com n;

……

• F(0) meio somando com -1.

Somando todas as somas n + 1 , vemos que há

• (n + 1) F(0) + n F(1) + … + F(n) formas de somar até -1, 0, …, ou n + 1.

Já que os dois métodos de contagem se referem ao mesmo numero , temos : (n + 1) F(0) + n F(1) + … + F(n) = F(n + 2) + F(n + 3) − (n + 2)

Finalmente, completamos a prova subtraindo a igualdade acima de n + 1 vezes a segunda igualdade. $\Box$

Número Tribonacci

Um número Tribonacci assemelha-se a um número de Fibonacci, mas em vez de começarmos com dois termos pré-definidos, a sequência é iniciada com três termos pré-determinados, e cada termo posterior é a soma dos três termos precedentes. Os primeiros números de uma pequena sequência Tribonacci são:

1, 1, 2, 4, 7, 13, 24, 44, 81, 149, 274, 504, 927, 1705, 3136, 5768, 10609, 19513, 35890, 66012, 121415, 223317, etc.

A Espiral

Na espiral formada pela folha de uma bromélia, pode ser percebida a sequência de Fibonacci, através da composição de quadrados com arestas de medidas proporcionais aos elementos da sequência, por exemplo: 1, 1, 2, 3, 5, 8, 13… , tendentes à razão áurea. Este mesmo tipo de espiral também pode ser percebida na concha do Nautilus marinho.

Repfigits

Um repfigit ou número de Keith é um número inteiro, superior a 9, tal que os seus dígitos, ao começar uma seqüência de Fibonacci, alcançam posteriormente o referido número. Um exemplo é 47, porque a seqüência de Fibonacci que começa com 4 e 7 (4, 7, 11, 18, 29, 47) alcança o 47. Outro exemplo é 197: 1+9+7= 17, 9+7+17= 33, 7+17+33= 57, 17+33+57= 107, 33+57+107= 197.

Um repfigit pode ser uma seqüência de Tribonacci se houver três dígitos no número, e de Tetranacci se o número tiver quatro dígitos, etc.

Alguns Números de Keith conhecidos: 14, 19, 28, 47, 61, 75, 197, 742, 1104, 1537, 2208, 2580, 3684, 4788, 7385, 7647, 7909, 31331, 34285…

Ligações externas

• «The Golden Section: Phi» 
• «Computing Fibonacci numbers on a Turing Machine» 
• «The Fibonacci Quarterly»  — um jornal acadêmico voltado ao estudo dos números de Fibonacci
• «Algoritmo de Fibonacci em O(lg n)» 
• «Veja como posicionar a sequência de fibonacci» 
• «Confira situações onde a Sequência de Fibonacci pode ser percebida.» 

obs=ve se tomem cuidado com esse site pois mtas pessoas podem modifica-lo