Sistema trifásico
Este artigo não cita fontes confiáveis. (Outubro de 2020) |

O sistema trifásico é a forma mais comum da geração, transmissão e distribuição de energia elétrica em corrente alternada. Este sistema incorpora o uso de três ondas senoidais balanceadas, defasadas em 120 graus entre si, de forma a equilibrar o sistema, tornando-a muito mais eficiente ao se comparar com três sistemas isolados. As máquinas elétricas trifásicas tendem a ser mais eficientes pela utilização plena dos circuitos magnéticos. As linhas de transmissão permitem a ausência do neutro, e o acoplamento entre as fases reduz significantemente os campos eletromagnéticos. Finalmente, o sistema trifásico permite a flexibilidade entre dois níveis de tensão. O sistema trifásico foi independentemente inventado por Galileo Ferraris, Mikhail Dolivo-Dobrovolski e Nikola Tesla nos meados do fim da década de 1880.
O sistema responsável pelo transporte de energia elétrica das unidades geradoras para as unidades consumidoras é composto basicamente por três subsistemas:
- Sistema de geração de energia
- Composta pelos elementos responsáveis pela conversão da energia de alguma fonte primária em energia elétrica e quaisquer outros componentes das unidades de geração.
- Sistema de transmissão
- Composta pelos elementos responsáveis pelo transporte da energia obtida dos vários sistemas de geração para o(s) sistema(s) de distribuição interligados pelo sistema de transmissão.
- Sistemas de distribuição
- Composta pelos elementos responsáveis pela adequação da energia para o uso de consumidores de grande, médio e pequeno porte.
A transmissão de energia elétrica é feita por meio de um sistema de transformadores e condutores elétricos também chamados de linhas de transmissão os quais transmitem a energia elétrica gerada nas unidades geradoras para as unidades consumidoras ou cargas.
O sistema de transmissão permite que a tensão eléctrica proveniente dos terminais dos geradores localizados nas unidades de geração alcance a alimentação das unidades de consumo atendidas pelo sistema.
Nos primórdios da implementação do sistema de transmissão de energia de longa distância, graças ao avanço tecnológico principalmente devido ao trabalho de Nikola Tesla foi utilizado o sistema alternado para as tensões e correntes, de forma a permitir o transporte de energia a longas distâncias sem perdas significativas a ponto de inviabilizar o processo.
Para a geração de tensões e correntes alternadas, utiliza-se geradores síncronos ou de indução que em teoria poderiam fornecer qualquer número de sinais de tensões e correntes alternadas igualmente defasadas entre si dependendo da construção dos geradores.
Por questões de praticidade, econômicas (economia de material) e técnicas (qualidade da energia fornecida), optou-se por utilizar o sistema trifásico.
Definição[editar | editar código-fonte]
Os sistemas trifásicos de energia elétrica são compostos de 3 tensões alternadas, no qual a energia elétrica é transmitida por meio da composição dos três sinais de tensão defasados de radianos (120°,1/3 de um ciclo).
A cada sinal de tensão alternada utilizado no sistema atribui-se o nome de fase, e portanto no sistema com 3 sinais temos um sistema trifásico
Originalmente o sistema é projetado para fornecer sinais de tensão senoidais no tempo, mas com o aumento das cargas eletrônicas (não lineares) a forma de onda do sinal de tensão sofre deformações o que causa o surgimento de harmônicos no sinal de tensão.
Configuração variável e definições básicas[editar | editar código-fonte]
Ao se trabalhar com sistemas trifásicos, é comum se definir algumas variáveis relacionadas a tensão e a corrente, para facilitar o cálculo da potência elétrica transmitida. Considerando um sistema trifásico com uma distribuição simétrica de cargas nas 3 fases e supondo que as formas de onda da tensão são senoidais temos:
Definindo
onde é o tempo, a frequência e a frequência angular.
Utilizando , as formas de onda para sistemas trifásicos são:
onde é valor eficaz dos sinais de tensão.
Quando se mede as tensões que estão aplicadas diretamente sobre as cargas temos o sinal de 'tensão de fase'. , e são as tensões de fase.
Ligação Estrela e Triângulo[editar | editar código-fonte]
As cargas trifásicas podem ser interligadas ao sistema de dois modos distintos:
- em estrela, também chamado de Y: um dos terminais das cargas é conectado a uma das fases do sistema enquanto o outro terminal é conectado a um ponto comum que é o neutro, aplicando as tensões de fase na carga.
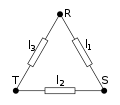
- em triângulo, também chamado de delta: nesta configuração um dos terminais das cargas é conectado a um outro terminal de outra carga e as fases do sistema são interligadas nos pontos de junção dos terminais da carga, aplicando as tensões de linha na carga..
-
Estrela (símbolo: Y)
-
Triângulo ou delta (símbolo: Δ)
Na conexão estrela podemos calcular o valor eficaz das 'tensões de linha' a partir dos valores eficazes das 'tensões de fase':
E as 'correntes de fase' são idênticas às 'correntes de linha', pois a corrente que circula por uma das cargas é a mesma que circula por uma das fases.
Na conexão triângulo ou delta a 'tensão de fase' é igual a 'tensão de linha' pois a tensão aplicada sobre cada uma das cargas é a diferença entre as tensões aplicadas às cargas vizinhas. E os valores eficazes das 'correntes de linha' podem ser calculadas com os valores eficazes das 'correntes de fase':
Pressupondo um sistema balanceado, que nem sempre ocorre na prática.
Transferência de potência constante[editar | editar código-fonte]
Uma propriedade importante do sistema trifásico é que a potência disponível para uma carga, , é constante no decorrer do tempo (válido para sistemas simétricos).
Para simplificar o cálculo, definimos uma variável intermediária adimensional:
Assim, substituindo:
Como o foi eliminado, observa-se que a potência total não varia com o tempo. Essa propriedade é essencial para manter grandes motores e geradores rodando suavemente.
Modelagem de sistemas trifásicos[editar | editar código-fonte]
Um sistema trifásico genérico pressupõe, no mínimo, o triplo de trabalho para modelar o circuito de cada fase e as interações entre eles. Um método de estudo consagrado são as componentes simétricas, no qual um circuito trifásico pode ser decomposto em três circuitos monofásicos. Cada circuito representa uma componente: zero, positiva e negativa (ou homopolar, direta e inversa).
Esta modelagem é usada em estudos de sistemas de potência, com as grandezas frequentemente representadas em pu.